数値積分-台形公式とシンプソンの公式の導出

微分は差分法を用いてコンピューターで数値計算することが出来ますが、積分をコンピューターで計算するときにどんな方法で行うのかといったことが今回のテーマです。

単純な数値積分 – 区分求積法

積分とは

積分とはつまり、面積を計算することです。

例えば$f(x) = ax$を区間$[0,b]$で積分を行うと、(1)式のようになります。

$$\int_0^b f(x) dx=\int_0^b ax dx = \frac{1}{2} \left[ a x^2 \right]_0^b = \frac{ab^2}{2} \tag{1}$$

この関係を図で描くと、$f(x) = ax$の式と$y = 0$の間における空間の面積である三角形になっていることが分かります。

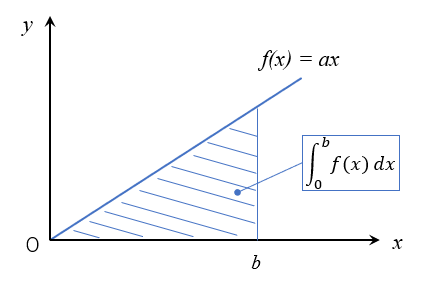
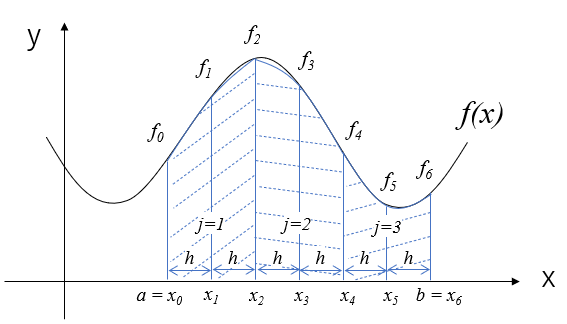
区分求積法

関数$f(x)$と$y=0$間の面積を求めればいいので、単純に考えると、積分区間$[a,b]$を分割し、分割した区間ごとに長方形の面積を計算して合計すれば良さそうですね。

これが区分求積法の考え方です。

絵で描くと以下のような感じです。

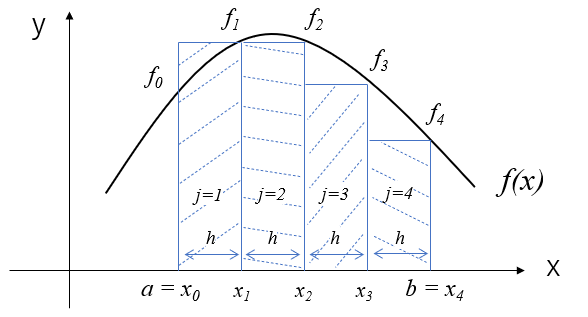
区分求積法は(2)式で計算できます。

$$\int_a^b f(x) dx \simeq \sum_{j=1}^{m} h \cdot f_{j} \tag{2}$$

$$h = (b-a)/m$$

区間を分割しないと長方形が一つだけになるのでまったく面積が合いませんね。

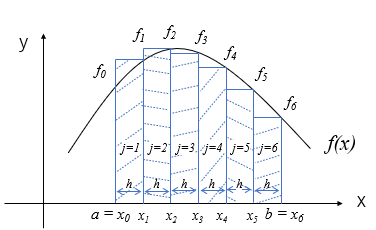
区間をある程度細かく分割しないとこの方法では面積計算の誤差が大きそうですよね。6分割した場合は4分割に比べて面積のずれが小さくなっていることが分かります。

後で他の数値積分法と比較しますが、区分求積法は分割数を多くしないとかなり数値誤差が出てしまう方法です。

ラグランジュの補間公式から数値積分

ラグランジュの補間公式の積分

関数$f(x)$を近似するラグランジュの補間公式$p_n(x)$は(3)式でした。

$$f(x) \simeq p_n(x) = \sum_{i=0}^{n} L_i(x) f_i \tag{3}$$

$$L_i(x) = \prod_{k=0, k\neq i}^{n} \frac{x-x_k}{x_i-x_k} \tag{4}$$

ということで、$p_n(x)$の積分を行えば、もとの関数$f(x)$を積分したことになりますね。

$$\int_a^b f(x) dx \simeq \int_a^b p_n(x) dx = \int_a^b \sum_{i=0}^{n} L_i(x) f_i dx = \sum_{i=0}^{n} \left\{ \int_a^b L_i(x) dx \right\} f_i \tag{5}$$

$$L_i(x) = \prod_{k=0, k\neq i}^{n} \frac{x-x_k}{x_i-x_k} \tag{6}$$

変数変換

ラグランジュの補間公式 $p_n(x)$はx軸上のサンプリング点が$x_0$から$x_n$まで$n$点あり、積分区間[a,b]と関連ずけると$a=x_0$、$b=x_n$となっています。また、各点間の間隔はステップ幅$h$です。

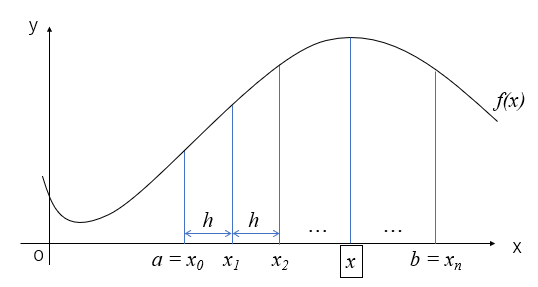
まず、範囲[a,b]のどこかの点$x$は初期値$x_0$とステップ幅$h$と実数$u$により(7)式で表すことが出来ます。この$x$は実数$u$により$x_0$と$x_1$の間を表す事が出来ます。

$$x = x_0 + hu \tag{7}$$

この(7)式の関係より、(6)式の$L_i(x)$の分子と分母はそれぞれ(8)式のように表すことができます。

$$\begin{eqnarray} 分子:x-x_k &=& (x_0+hu)-(x_0+hk)=(u-k)h \\ 分母:x_i-x_k &=& (x_0+hi)-(x_0+hk)=(i-k)h \end{eqnarray} \tag{8}$$

この(8)式より、$L_i(x)$は(9)式になります。分母が$(i=i)$にならないように展開され、これと同じように分子も展開されています。

$$L_i(x) = \prod_{k=0, k \neq i}^{n} \frac{u-k}{i-k} = \frac{(u – 0)\cdots(u – (i – 1))\cdot(u – (i + 1))\cdots(u – (n – 1))(u – n)}{(i – 0)\cdots(i – (i – 1))\cdot(i – (i + 1))\cdots(i -(n – 1))(i – n)} \tag{9}$$

次の、分母を$i-i$となる前後に分けて考えます。

まず前の部分である$(i – 0)(i – 1)(i – 2)\cdots(i – (i – 1))$は最終項が$(i – (i – 1)) = 1$になっているので、$i! = (i – 0)(i – 1)\cdots2\cdot1$です。

そして後ろの部分である$(i – (i + 1))(i – (i + 2))\cdots(i – (n – 1))(i – n)$ですが、これを逆順に並べると、

$$(i-n+0)(i-n+1)(i-n+2)\cdots(i-i-2)(i-i-1) =\\(i-n+0)(i-n+1)(i-n+2)\cdots-2\cdot-1$$

そして、各項に$-1$を掛けることで、

$$(-1)^{(n-i)} \times (n-i-0)(n-i-1)(n-i-2)\cdots2\cdot1 =(-1)^{(n-i)} \times (n-i)!$$

となります。よって、$L_i(x)$は(10)式で表すことで出来ます。

$$L_i(x) = \prod_{k=0, k \neq i}^{n} \frac{u – k}{i – k} = \frac{(u – 0)(u – 1)\cdots(u – (i – 1))\cdot(u – (i + 1))\cdots(u – (n – 1))(u – n)}{i! \cdot(-1)^{n – i}\cdot(n – i)!} \tag{10}$$

(5)式の積分は(11)式のように$L_i(x)$を積分しています。

$$\sum_{i=0}^{n} \left\{ \int_a^b L_i(x) dx \right\} f_i \tag{11}$$

$L_i(x)$は$x = x_0 + hu$の変換により(10)式で$u$の式となっているため、

$$\frac{dx}{du} = h \Rightarrow dx = h du$$

また積分の範囲は$u=(x-x_0)/h$の関係より、$u$は区間$[0,n]$での積分となります。

$$\begin{array}{|c|c|} \hline x & u \\ \hline \hline a & (a-x_0)/h = 0 \\ \hline b & (b-x_0)/h = n\\ \hline \end{array}$$

以上の変換により、数値積分は(12)式と表すことが出来ます。

$$\sum_{i=0}^{n} \left\{ \int_a^b L_i(x) dx \right\} f_i =\\ h\sum_{i=0}^{n} \left\{ \frac{(-1)^{(n-i)}}{i!\cdot(n-i)!} \int_0^n (u-0)(u-1)\cdots(u-(i-1))\cdot(u-(i+1))\cdots(u-n) du \right\} f_i \tag{12}$$

そして、$C_i$を(13)式とすると、(12)式は(14)式で表すことが出来ます。

$$\begin{eqnarray} C_i &=& \frac{(-1)^{(n-i)}}{i!\cdot(n-i)!} \int_0^n (u-0)(u-1)\cdots(u-(i-1))\cdot(u-(i+1))\cdots(u-n) du \\ &=& \frac{(-1)^{(n-i)}}{i!\cdot(n-i)!} \int_0^n \prod_{k=0, k\neq i}^{n}(u-k) du \end{eqnarray} \tag{13}$$

$$\int_a^b f(x) dx \simeq h \sum_{i=0}^{n} C_i f_i = h(C_0 f_0 + C_1 f_1 + \cdots + C_n f_n) \tag{14}$$

この(14)式の$n$を変更することで、台形公式とシンプソンの公式を導くことが出来ます。

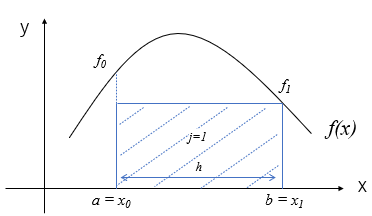
台形公式の導出

(14)式で$n=1$にします。

$$\int_a^b f(x) dx \simeq h(C_0 f_0+C_1 f_1)$$

それぞれの$C_i$を計算すると、

$$C_0 = \frac{(-1)^{(1-0)}}{0!\cdot(1-0)!} \int_0^1 (u-1) du = -1 \int_0^1 (u-1) du = – \left[ \frac{1}{2} u^2 -u \right]_0^1 = \frac{1}{2}$$

$$C_1 = \frac{(-1)^{(1-1)}}{1!\cdot(1-1)!} \int_0^1 u du = \int_0^1 u du = \left[ \frac{1}{2} u^2 \right]_0^1 = \frac{1}{2}$$

以上の計算より、$n=1$のときは、積分の計算が(15)式になります。

$$\int_a^b f(x) dx \simeq \frac{h}{2}(f_0 + f_1) \tag{15}$$

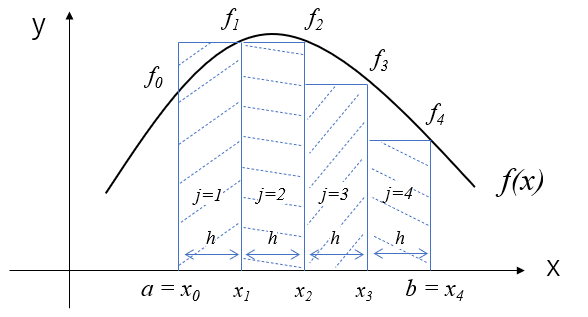
この関係は次の図のようになっていて、台形の面積の計算と同じなため、台形公式と呼ばれています。

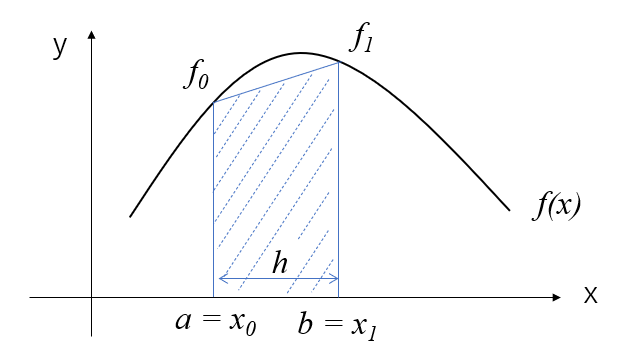
しかし、このままでは積分計算の誤差が大きいため、(16)式のように区間$[a,b]$を$m$等分し、それぞれの区間で台形公式により面積を求めて加算するようにします。

$$\int_a^b f(x) dx \simeq \sum_{j=1}^{m} \frac{h}{2}(f_{j-1} + f_j) \tag{16}$$

$$h = (b-a)/m$$

絵で描くと、こんなイメージです。区分求積法に比べると実際の区間$[a,b]$における$f(x)$の面積を良く表すことが出来ていますね。それでも若干のずれは生じています。

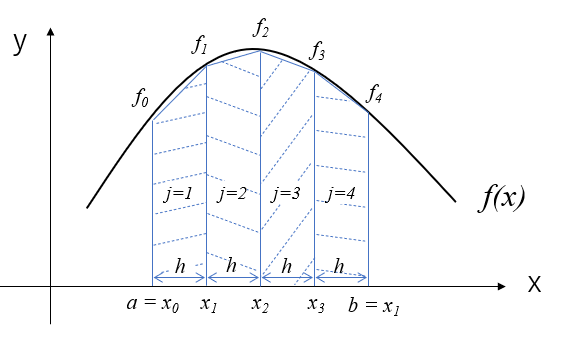
シンプソンの公式の導出

(14)式で$n=2$にします。

$$\int_a^b f(x) dx \simeq h(C_0 f_0+C_1 f_1 + C_2 f_2)$$

それぞれの$C_i$を計算すると

$$C_0 = \frac{(-1)^{(2-0)}}{0!\cdot(2-0)!} \int_0^2 (u-1)(u-2) du = \frac{1}{2} \left[\frac{1}{3}u^3 – \frac{3}{2}u^2 +2u\right]_0^2 = \frac{1}{3}$$

$$C_1 = \frac{(-1)^{(2-1)}}{1!\cdot(2-1)!} \int_0^2 u(u-2) du = – \left[\frac{1}{3}u^3 – u^2\right]_0^2 = \frac{4}{3}$$

$$C_2 = \frac{(-1)^{(2-2)}}{2!\cdot(2-2)!} \int_0^2 u(u-1) du = \frac{1}{2} \left[\frac{1}{3}u^3 – \frac{1}{2}u^2 \right]_0^2 = \frac{1}{3}$$

以上の計算により、$n=2$では積分の計算が(17)式になります。

$$\int_a^b f(x) dx \simeq \frac{h}{3}(f_0+4f_1 +f_2) \tag{17}$$

これはラグランジュの補間公式で3点を使って近似式を作成したことになるため、２次式となります。図で描くと次のようなイメージです。この式をシンプソンの公式といいます。

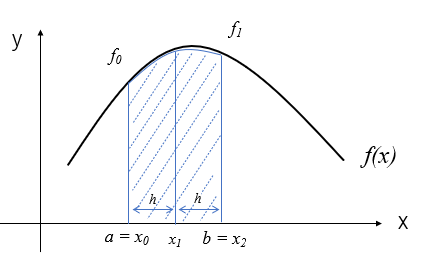
図では結構精度よく積分出来ているように見えますが、３次式、４次式のように次数が多くなると計算誤差が大きくなるため、台形公式と同じように(18)式のように区間を分割して積分計算を行います。各区間で$n=2$ずつデータを使用するため、区間$[a,b]$を$2m$等分します。

$$\int_a^b f(x) dx \simeq \sum_{j=1}^{m} \frac{h}{3}(f_{2j-2}+4f_{2j-1} +f_{2j}) \tag{18}$$

$$h = (b-a)/2m$$

図で描くとこんなイメージです。各区間を２次式で近似して計算するためかなり精度良く積分計算を行うことが出来ます。

計算比較

では、区分求積法、台形公式、シンプソンの公式で数値計算を行いましょう。

比較に用いる式 – 3次式

(19)式を数値計算し、それぞれの結果を比較しています。

$$f(x) = 4x^3 + 12 x^2 -5x + 1 \tag{19}$$

(19)式を区間$[-2,2]$で定積分を行います。比較のため解析解を計算すると、答えは$“68″$です。

$$\begin{eqnarray} \int_{-2}^{2} f(x) dx &=& \int_{-2}^{2} 4x^3 + 12 x^2 -5x + 1 dx \ &=& \left[ x^4 + 4 x^3 -\frac{5}{2} x^2 +x \right]_{-2}^{2} \ &=& 68 \end{eqnarray}$$

数値計算 Python プログラム

数値計算はPythonで行います。それぞれの数値計算の関数を定義します。

区分求積法

import numpy as np

def RiemannSum(f, a, b, m):
    h = (b - a) / m
    x_array = np.linspace(a,b,m+1)
    sum = 0
    for xi in x_array[1:]:
        sum += h * f(xi) 
    return sum

台形公式

import numpy as np

def TrapezoidalRule(f,a,b,m):
    h = (b-a)/m
    x_array = np.linspace(a,b,m+1)
    sum = 0
    for i in range(1,len(x_array)):
        fp = f(x_array[i-1])
        fn = f(x_array[i])
        sum += h*(fp + fn) /2
    return sum

シンプソンの公式

import numpy as np

def SimpsonRule(f,a,b,m):
    n = int(m/2)
    x_array = np.linspace(a,b,m+1)
    h = (b-a)/m
    sum = 0
    for i in range(1,n+1):
        f1 = f(x_array[2*i -2])
        f2 = f(x_array[2*i -1])
        f3 = f(x_array[2*i])
        sum += h*(f1 + 4*f2 + f3)/3
    return sum

計算比較 – 3次式

分割数を$4,8,12$の３つでそれぞれの方法で計算します。

分割数	区分求積法	台形公式	シンプソンの公式
4	98.0	76.0	68.0
8	81.0	70.0	68.0
12	76.2	68.9	68.0

結果は、シンプソンの公式は分割数が少なくても解析解の$“68″$を計算できています。区分求積法、台形公式は分割数が多くなるにつれて解へ近づいていますが、収束が遅いですね。

また、区分求積法は精度が悪いです。

比較に用いる式 – 三角関数

次は(20)式を数値積分して比較を行います。

$$f(x) = sin(5x) \tag{20}$$

定積分区間を$[0,\pi]$とすると、解析解は$“0.4″$です。

ところで周波数を5倍にしているのは、関数$f(x)$を急峻にしたいからです。区分求積法、台形公式、シンプソンの公式は近似なので、急に変化する関数には対応できません。それを確認するためです。

計算比較 – 三角関数

分割数を$4,8,12,20$の４つでそれぞれの方法で計算します

分割数	区分求積法	台形公式	シンプソンの公式
4	-0.325	-0.325	-0.957
8	0.262	0.262	0.458
12	0.341	0.341	0.408
20	0.379	0.379	0.401

分割数が少ないとシンプソンの公式でも大きくずれていますね。

区分求積法と台形公式は同じ結果となっています。区分求積法よりも台形公式が必ず優れているとは言えない例です。

まとめ

今回紹介した台形公式とシンプソンの公式は”ニュートン・コーツの公式”と呼ばれる数値計算の方法です。この方法はラグランジュの補間公式に基づいているので、点数が多いと元の関数を良く表すことが出来ているいます。そのため、シンプソンの公式の計算結果が良かったということですね。

今回説明を行った数値積分は、離散時間フーリエ変換などに利用されます。