ポアソン分布に従う確率事象が次に発生するまでの期間は指数分布に従います。
確率密度関数、期待値、分散の式
確率密度関数と分布
指数分布の確率変数\(X\)は次の確率密度関数に従います。
$$
f(x|\lambda) = \lambda e^{-\lambda x}
$$
\(\lambda\)は単位時間当たりの発生回数で、\(x\)は次にその事象が生じるまでの期間を表します。
そして、確率を計算するために、確率密度関数を積分した累積分布関数\(F(X)\)が必要です。
$$
\begin{eqnarray}
F(X) &=& P(X \leq x) = \int_0^x f(x| \lambda) dx \\
&=& \lambda \int_0^x e^{-\lambda x} dx \\
&=& \lambda \left[ -\frac{e^{-\lambda x}}{\lambda} \right]_0^x \\
F(X) &=& 1 – e^{-\lambda x}
\end{eqnarray}
$$
例えば、年間10回噴火する活火山があるとします。
一度噴火を観察してからもう一度噴火をするまで何日間の観測が必要でしょうか?
単位時間を365日として、噴火を次に観測出来る日が5日以内である確率は、
まず\(\lambda = 10\)です。それから、5日を単位時間中の期間に変換するので\(x=5 / 365\)です。ここから
$$
F(X) = 1 – e^{-\lambda x} = 1 – e^{-10 \times 5 / 365} \simeq 0.13
$$
のように計算できます。13%ですね。
では、5日以内に噴火を観測できない確率はいくつでしょうか?
これは\( 1 – F(X)\)で計算できるので、
$$
1-F(X) = 1 – 0.13 = 0.87
$$
となり、87%です。
次に噴火が観測出来る日\(x\)をパラメータに取り、 累積分布関数を計算します。
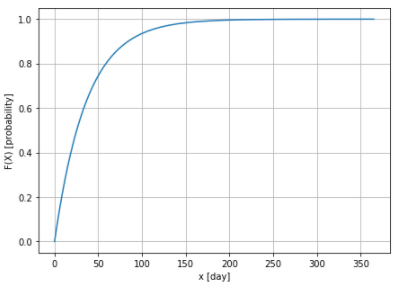
こんな感じのグラフになります。ここから大体200日観測を行うと、100%観測出来ることになりますね。
25日観測を行うと、50%の確率で噴火が観測出来る事になります。
横軸を単位時間を1に取りプロットした図は以下のようになります。
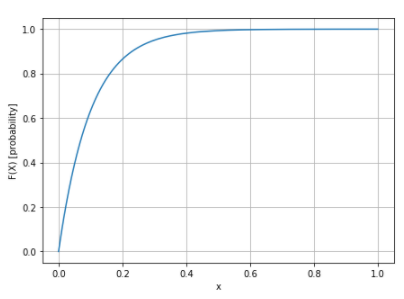
期待値と分散
指数分布の期待値\(E[X]\)と分散\(V[X]\)は次の式です。
$$
\begin{eqnarray}
E[X] &=& \frac{1}{\lambda} \\
V[X] &=& \frac{1}{\lambda^2}
\end{eqnarray}
$$
期待値、分散の導出
期待値 \(E[X]\)の導出
指数分布の確率変数\(X\)は実数なので
$$
\begin{eqnarray}
E[X] &=& \int_{0}^{\infty} x \lambda e^{-\lambda x} dx \\
&=& \lambda \int_{0}^{\infty} x e^{-\lambda x} dx
\end{eqnarray}
$$
これに部分積分を適用します。
部分積分
$$
\int f^\prime(x) g(x) dx = f(x) g(x) – \int f(x) g^\prime(x) dx
$$
次のように\(f^\prime(x), g(x)\)を決めます。
$$
f^\prime(x) = e^{-\lambda x} , g(x) =x
$$
すると
$$
\begin{eqnarray}
E[X] &=& \lambda \int_{0}^{\infty} x e^{\lambda x} dx \\
&=& \lambda \left[-\frac{x}{\lambda} e^{-\lambda x} \right]_0^{\infty} + \int_0^\infty e^{-\lambda x} dx \\
&=& -\frac{\infty}{e^{\lambda \infty}} + \frac{0}{e^0} – \frac{1}{\lambda} \left[e^{-\lambda x} \right]_0^\infty \\
&=& -\frac{1}{\lambda} \left\{ \frac{1}{e^{\lambda \infty}} – \frac{1}{e^0} \right\} \\
E[X]&=& \frac{1}{\lambda}
\end{eqnarray}
$$
分散\(V[X]\)の導出
次の方法で分散\(V[X]\)を求めます。
$$
V[X] = E[X^2] – E[X]^2
$$
\(E[X^2]\)は次のようになります。
$$
\begin{eqnarray}
E[X^2] &=& \int_0^\infty x^2 \lambda e^{-\lambda x} dx \\
&=& \lambda \int_0^\infty x^2 \left(-\frac{1}{\lambda} e^{-\lambda x} \right)^\prime dx \\
&=& \lambda \left[ -\frac{x^2}{\lambda} e^{-\lambda x} \right]_0^\infty + \lambda \int_0^\infty \frac{2x}{\lambda} e^{-\lambda x} dx \quad \leftarrow 部分積分 \\
&=& \left( -\frac{ \infty^2}{e^{\lambda \infty}} + 0 \right) + \frac{2}{\lambda} \int_0^\infty x \lambda e^{-\lambda x} dx \\
&=& \frac{2}{\lambda} E[X] \\
E[X^2]&=& \frac{2}{\lambda^2}
\end{eqnarray}
$$
これより、
$$
\begin{eqnarray}
V[X] &=& E[X^2] – E[X]^2 \\
&=& \frac{2}{\lambda^2} – \frac{1}{\lambda^2} \\
V[X] &=& \frac{1}{\lambda^2}
\end{eqnarray}
$$

コメント