2項分布の試行回数\(n\)が大きくなり、確率\(\theta\)が小さくなったものがポアソン分布です。
例えば、1分ごとに夜空を見上げて、その時に流れ星が見える確率などです。
確率分布、期待値、分散
確率分布
ポアソン分布に従う確率変数\(X\)は次の確率関数の式に従います。
$$
f(x | \lambda) = \frac{e^{-\lambda} \lambda^x}{x!}, \quad 0 \leq x \leq \infty, \quad xは整数
$$
\(\lambda\)は単位時間当たりの発生数で\(\lambda = n \theta\)です。
例1
例えば、ある活火山が年間40回噴火します。
7日間その火山を観察して、何回噴火を観察することが出来るでしょうか?
この場合、確率変数$X$は観察できる噴火の回数を表します。
まず噴火確率\(\theta\)を計算します。そうすると一日平均では40回/365日 = 0.1回/日になります。
\(\theta = 0.1, n = 7\)なので\(\lambda = 0.7\)です。よってこの\(\lambda\)は7日当りの噴火回数になります。
噴火回数が確率変数\(X\)なので、これをパラメータにして、0回から9回までのグラフは次のようになります。

この結果から、単位時間(7日)観察しても、噴火の回数を観察できるのは、0回が最も多いとなります。
例2
年間120回の噴火をしている火山があり、50日間の観察で何度噴火を観測出来るでしょうか?
単位時間を50日間に変換するため、まず一日当りの噴火確率\(\theta\)を計算します。
$$
\theta = 120 / 365 = 0.33
$$
これに単位時間としたい50日(\(n\))を掛け合わせて\(\lambda\)を算出します。
$$
\lambda = n \times \theta = 50 \times 0.33 = 16.4
$$
確率変数\(X\)をパラメータにとり、単位時間(50日)当たりに観測出来る噴火回数の確率を計算すると、次のような図になります。
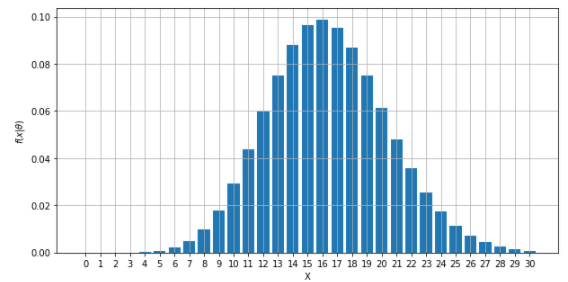
50日間観測すると、16回の噴火回数の観測数が最も多い確率となりました。
期待値、分散
ポアソン分布の期待値\(E[X]\)と分散\(V[X]\)は次の式です。
$$
\begin{eqnarray}
E[X] &=& \lambda \\
V[X] &=& \lambda
\end{eqnarray}
$$
確率分布、期待値、分散の導出
確率分布の導出
ポアソン分布は2項分部の試行回数\(n\)が大きくなり、確率\(\theta\)が小さくなったものです。なので、2項分部の\(n \to \infty, \theta \to 0\)の極限を取り、それがポアソン分布になることを導出してみましょう。
$$
\lim_{n \to \infty, \theta \to 0 }\left\{{}_n \mathrm{C} _x \theta^x(1-\theta)^{n-x} \right\}\to \frac{e^{-\lambda} \lambda^x}{x!}
$$
(1) \({}_n \mathrm{C} _x\)部
組み合わせ部分は次のように展開できます。
$$
\begin{eqnarray}
{}_c \mathrm{C}_x &=& \frac{n!}{x!(n-x)!)} \\
&=& \frac{1}{x!} \frac{n \cdot (n-1) \cdots \cdot (n-x) \cdots (n-(n-1))}{(n-x)\cdot(n-x-1) \cdots (n-x -(n-x-1))} \\
&=& \frac{1}{x!} n \cdot (n-1) \cdots (n-x+1)
\end{eqnarray}
$$
(2) \( \theta^x\)部
\( \lambda = n \theta\)より\( \theta = \lambda / n\)です。これより
$$
\theta^x = \frac{\lambda^x}{n^x}
$$
(3) \( (1-\theta)^{n-x}\)部
\( (1-\theta)^{n-x} = (1 – \theta)^n \cdot (1-\theta)^{-x}\)と分解して考えます。
まず\( (1-\theta)^n\)について展開します。
$$
(1 – \theta)^n = \left( 1 – \frac{\lambda}{n} \right)^n
$$
指数関数の定義は次のようになっているので、
$$
\begin{eqnarray}
e^x &=& 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} \cdots \
&=& \lim_{n \to \infty} \left(1 + \frac{x}{n}\right)^n
\end{eqnarray}
$$
\((1-\lambda/n)^n\)を\(n \to \infty\)とすると
$$
\lim_{n \to \infty} \left( 1 + \frac{-\lambda}{n} \right)^n = e^{-\lambda}
$$
つぎに\( (1 – \theta)^{-x}\)について展開します。
$$
(1-\theta)^{-x} = (1-\lambda/n)^{-x}
$$
\(n \to \infty\)とし、\(x\)は整数なので
$$
\lim_{n \to \infty}\left(1- \frac{\lambda}{n}\right)^{-x} = 1 ^{-x} = 1
$$
以上より、
$$
(1-\theta)^{n-x} = e^{-\lambda}
$$
(1),(2),(3)の適用
上で展開した(1)、(2)、(3)の結果を2項分布の式に当てはめます。
$$
{}_n \mathrm{C} _x \theta^x(1-\theta)^{n-x} = \frac{n \cdot(n-1) \cdots (n-x+1)}{n^x} \frac{e^{-\lambda} \lambda^x}{x!}
$$
ここで、
$$
\begin{eqnarray}
\frac{(n-0)\cdot(n-1) \cdots (n-x+1)}{n^x} &=& \frac{n}{n} \frac{n-1}{n} \cdots \frac{n-x+1}{n} \\
&=& 1 \cdot \left(1 + \frac{-1}{n} \right) \cdots \left( 1 +\frac{-x+1}{n} \right)
\end{eqnarray}
$$
\(n \to \infty\)とすることにより
$$
\lim_{n \to \infty} \left\{ 1 \cdot \left(1 + \frac{-1}{n} \right) \cdots \left( 1 +\frac{-x+1}{n} \right) \right\}= \left\{ 1 \cdot 1 \cdots 1 \right\} = 1
$$
以上の式展開により、2項分布の極限(\( n \to \infty , \theta\to 0\) )を取ると、ポアソン分布になることが導出出来ました。
$$
\lim_{n \to \infty, \theta \to 0 }\left\{{}_n \mathrm{C} _x \theta^x(1-\theta)^{n-x} \right\}\to \frac{e^{-\lambda} \lambda^x}{x!}
$$
期待値\(E[X]\)の導出
ポアソン分布の確率変数\(X\)は整数です。よって
$$
\begin{eqnarray}
E[X] &=& \sum_{x = 0}^{\infty} x \cdot \frac{e^{-\lambda} \lambda^x}{x!} \\
&=& \sum_{x = 0}^{\infty} \lambda \cdot \frac{e^{-\lambda} \lambda^{(x-1)}}{(x-1)!} \\
&=& \lambda e^{-\lambda} \sum_{x = 0}^{\infty} \frac{\lambda^{(x-1)}}{(x-1)!} \quad \leftarrow y = x-1 \\
& =& \lambda e^{-\lambda} \sum_{y = 0}^{\infty} \frac{\lambda^{y}}{y!}
\end{eqnarray}
$$
ここで指数関数の定義より
$$
\begin{eqnarray}
e^x &=& 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} \cdots \\
&=& \frac{x^0}{0!} + \frac{x^1}{1!} + \frac{x^2}{2!} + \frac{x^3}{3!} \cdots \\
&=& \sum_{y=0}^{\infty} \frac{x^y}{y!}
\end{eqnarray}
$$
$$
\begin{eqnarray}
E[X] &=& \lambda e^{-\lambda} \sum_{y = 0}^{\infty} \frac{\lambda^{y}}{y!} \\
&=& \lambda e^{-\lambda} e^{\lambda} \\
E[X] &=& \lambda
\end{eqnarray}
$$
分散\(V[X]\)の導出
分散は次の計算から求めることが出来ます。\(E[X] = \lambda\)なので、\(E[X^2]\)を求めて分散を導出します。
$$
V[X] = E[X^2] – E[X]^2
$$
\(E[X^2]\)の計算
$$
\begin{eqnarray}
E[X^2] &=& \sum_{x = 0}^{\infty} x^2 \frac{e^{-\lambda} \lambda^x}{x!} \\
&=& \sum_{x = 0}^{\infty} (x (x-1) + x) \frac{e^{-\lambda} \lambda^x}{x!} \\
&=& \sum_{x = 0}^{\infty} (x (x-1)) \frac{e^{-\lambda} \lambda^x}{x!} +\sum_{x = 0}^{\infty} x \frac{e^{-\lambda} \lambda^x}{x!} \\
&=& \sum_{x = 0}^{\infty} \frac{e^{-\lambda} \lambda^x}{(x-2)!} +E[X] \\
&=& \lambda ^2 e^{-\lambda} \sum_{x = 0}^{\infty} \frac{\lambda^{x-2}}{(x-2)!} +E[X] \\
&=& \lambda ^2 e^{-\lambda} \sum_{y = 0}^{\infty} \frac{\lambda^{y}}{y!} +E[X] \quad \leftarrow ( y = x-2) \\
&=& \lambda ^2 e^{-\lambda} e^{\lambda} +E[X] \quad \leftarrow 指数関数の定義より \\
&=& \lambda ^2 + E[X] \\
E[X^2] &=& \lambda ^2 + \lambda
\end{eqnarray}
$$
これより、分散は次のように算出できます。
$$
V[X] = E[X^2] – E[X]^2 = \lambda^2 + \lambda – \lambda^2 = \lambda
$$

コメント