\(LU\)分解は、方程式\(Ax = b\)の解を計算に工夫が必要な逆行列を求める方法でなく、機械的に簡単な計算で求められる方法です。
ではどのように\(A = LU\)へと分解するのか、具体的に計算を行いながら分解アルゴリズムを見てみましょう。Pivot付きの計算も行うので少し複雑ですが、実装してみれば簡単なことが分かります。
LU分解の基本的な方法
まずは基本的な行列で\(LU\)分解を行ってみます。
\(A = LU \)の行列を(1)式のように置いて考えます。
$$
\left(\begin{array}{cccc}
a_{11} & a_{12} & a_{13} & a_{14} \\
a_{21} & a_{22} & a_{23} & a_{24} \\
a_{31} & a_{32} & a_{33} & a_{34} \\
a_{41} & a_{42} & a_{43} & a_{44}
\end{array}\right) =
\left(\begin{array}{cccc}
1 & 0 & 0 & 0 \\
l_{21} & 1 & 0 & 0 \\
l_{31} & l_{32} & 1 & 0 \\
l_{41} & l_{42} & l_{43} & 1
\end{array}\right)
\left(\begin{array}{cccc}
u_{11} & u_{12} & u_{13} & u_{14} \\
0 & u_{22} & u_{23} & u_{24} \\
0 & 0 & u_{33} & u_{34} \\
0 & 0 & 0 & u_{44}
\end{array}\right) \tag{1}
$$
1段目
この(1)式のA行列の1行目の計算から、
$$
\left(\begin{array}{cccc}
a_{11} & a_{12} & a_{13} & a_{14} \\
\hline
a_{21} & a_{22} & a_{23} & a_{24} \\
a_{31} & a_{32} & a_{33} & a_{34} \\
a_{41} & a_{42} & a_{43} & a_{44}
\end{array}\right) =
\left(\begin{array}{cccc}
1 & 0 & 0 & 0 \\
\hline
l_{21} & 1 & 0 & 0 \\
l_{31} & l_{32} & 1 & 0 \\
l_{41} & l_{42} & l_{43} & 1
\end{array}\right)
\left(\begin{array}{c|c|c|c}
u_{11} & u_{12} & u_{13} & u_{14} \\
0 & u_{22} & u_{23} & u_{24} \\
0 & 0 & u_{33} & u_{34} \\
0 & 0 & 0 & u_{44}
\end{array}\right)
$$
U行列の1行目は(2)式のように求まります。
$$
\begin{eqnarray}
a_{11} &=& u_{11} \\
a_{12} &=& u_{12} \\
a_{13} &=& u_{13} \\
a_{14} &=& u_{14}
\end{eqnarray} \tag{2}
$$
続いてA行列の1列目から
$$
\left(\begin{array}{c|ccc}
a_{11} & a_{12} & a_{13} & a_{14} \\
a_{21} & a_{22} & a_{23} & a_{24} \\
a_{31} & a_{32} & a_{33} & a_{34} \\
a_{41} & a_{42} & a_{43} & a_{44}
\end{array}\right) =
\left(\begin{array}{cccc}
1 & 0 & 0 & 0 \\ \hline
l_{21} & 1 & 0 & 0 \\ \hline
l_{31} & l_{32} & 1 & 0 \\ \hline
l_{41} & l_{42} & l_{43} & 1
\end{array}\right)
\left(\begin{array}{c|ccc}
u_{11} & u_{12} & u_{13} & u_{14} \\
0 & u_{22} & u_{23} & u_{24} \\
0 & 0 & u_{33} & u_{34} \\
0 & 0 & 0 & u_{44}
\end{array}\right)
$$
L行列の1列目は(3)式のように求まります。
$$
\begin{eqnarray}
a_{11} = l_{11} u_{11} &\Rightarrow& l_{11} = a_{11} / u_{11} = 1 \\
a_{21} = l_{21} u_{11} &\Rightarrow& l_{21} = a_{21} / u_{11} \\
a_{31} = l_{31} u_{11} &\Rightarrow& l_{31} = a_{31} / u_{11} \\
a_{41} = l_{41} u_{11} &\Rightarrow& l_{41} = a_{41} / u_{11}
\end{eqnarray} \tag{3}
$$
ここで\(l_1, u_1\)を(4)式のように定義すると
$$
l_1 = (1, l_{21}, l_{31}, l_{41})^T, u_1 = (u_{11}, u_{12}, u_{13}, u_{14}) \tag{4}
$$
\(l_1 u_1\)は(5)式となるので、
$$
\begin{eqnarray}
l_1 u_1 &=&
\left(\begin{array}{c}
1 \\ l_{21} \\ l_{31} \\ l_{41}
\end{array}\right)
\left(\begin{array}{cccc}
u_{11} & u_{12} & u_{13} & u_{14}
\end{array}\right) \\ &=&
\left(\begin{array}{cccc}
u_{11} & u_{12} & u_{13} & u_{14} \\
l_{21} u_{11} & l_{21} u_{12} & l_{21} u_{13} & l_{21} u_{14} \\
l_{31} u_{11} & l_{31} u_{12} & l_{31} u_{13} & l_{31} u_{14} \\
l_{41} u_{11} & l_{41} u_{12} & l_{41} u_{13} & l_{41} u_{14}
\end{array}\right)\\ &=&
\left(\begin{array}{cccc}
a_{11} & a_{12} & a_{13} & a_{14} \\
a_{21} & l_{21} u_{12} & l_{21} u_{13} & l_{21} u_{14} \\
a_{31} & l_{31} u_{12} & l_{31} u_{13} & l_{31} u_{14} \\
a_{41} & l_{41} u_{12} & l_{41} u_{13} & l_{41} u_{14}
\end{array}\right)
\end{eqnarray} \tag{5}
$$
\(A – l_1 u_1 = A_{(2)}\)として、\(A_{(2)}\)は(6)式となります。
$$
A_{(2)} =
\left(\begin{array}{c|ccc}
0 & 0 & 0 & 0 \\ \hline
0 & a_{22(2)} & a_{23(2)} & a_{24(2)} \\
0 & a_{32(2)} & a_{33(2)} & a_{34(2)} \\
0 & a_{42(2)} & a_{43(2)} & a_{44(2)}
\end{array}\right) \tag{6}
$$
以上の関係から\(A = A_{(1)}\)として、\(A_{(1)} = l_1 u_1 + A_{(2)}\)となります。
2段目
\(A_{(2)}\)は\(A_{(1)}\)から一つ縮小した関係なので、これをさらにLU分解を行います。\(A_{(2)}\)より、LUも(7)式のように一つ縮小した形を考えます。
$$
\left(\begin{array}{c|ccc}
0 & 0 & 0 & 0 \\ \hline
0 & a_{22(2)} & a_{23(2)} & a_{24(2)} \\
0 & a_{32(2)} & a_{33(2)} & a_{34(2)} \\
0 & a_{42(2)} & a_{43(2)} & a_{44(2)}
\end{array}\right)=
\left(\begin{array}{c|ccc}
0 & 0 & 0 & 0 \\ \hline
0 & 1 & 0 & 0 \\
0 & l_{32} & 1 & 0 \\
0 & l_{42} & l_{43} & 1
\end{array}\right)
\left(\begin{array}{c|ccc}
0 & 0 & 0 & 0 \\ \hline
0 & u_{22} & u_{23} & u_{24} \\
0 & 0 & u_{33} & u_{34} \\
0 & 0 & 0 & u_{44}
\end{array}\right) \tag{7}
$$
この(7)式より、1段目と同じようにU行列の2行目は(8)式、L行列の2列目は(9)式のように求まります。
$$
\begin{eqnarray}
a_{22(2)} &=& u_{22} \\
a_{23(2)} &=& u_{23} \\
a_{24(2)} &=& u_{24}
\end{eqnarray} \tag{8}
$$
$$
\begin{eqnarray}
a_{22(2)} = l_{22} u_{22} &\Rightarrow& l_{22} = a_{22(2)} / u_{22} = 1 \\
a_{32(2)} = l_{32} u_{22} &\Rightarrow& l_{32} = a_{32(2)} / u_{22} \\
a_{42(2)} = l_{42} u_{22} &\Rightarrow& l_{42} = a_{42(2)} / u_{22}
\end{eqnarray} \tag{9}
$$
ここで、\(l_2, u_2\)を(10)式のように定義して、
$$
l_2 = (0, 1, l_{32}, l_{42})^T, u_1 = (0, u_{22}, u_{23}, u_{24}) \tag{10}
$$
\(A_{(2)} – l_2 u_2 = A_{(3)}\)とすると\(A_{(3)}\)は(11)式のよう一つ縮小した形になります。
$$
A_{(3)} =
\left(\begin{array}{cc|cc}
0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 \\ \hline
0 & 0 & a_{33(3)} & a_{34(3)} \\
0 & 0 & a_{43(3)} & a_{44(3)}
\end{array}\right) \tag{11}
$$
\(A_{(2)} = l_2 u_2 + A_{(3)}\)より、\(A_{(1)} = l_1 u_1 + l_2 u_2 + A_{(3)}\)という関係になります。
3段目
\(A_{(2)}\)から一つ縮小した\(A_{(3)}\)をさらにLU分解を行います。\(A_{(3)}\)の関係から\(LU\)行列も(12)式のようになります。
$$
\left(\begin{array}{cc|cc}
0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 \\ \hline
0 & 0 & a_{33(3)} & a_{34(3)} \\
0 & 0 & a_{43(3)} & a_{44(3)}
\end{array}\right)=
\left(\begin{array}{cc|cc}
0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 \\ \hline
0 & 0 & 1 & 0 \\
0 & 0 & l_{43} & 1
\end{array}\right)
\left(\begin{array}{cc|cc}
0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 \\ \hline
0 & 0 & u_{33} & u_{34} \\
0 & 0 & 0 & u_{44}
\end{array}\right) \tag{12}
$$
(12)式の関係から\(U\)行列の3行目は(13)式、\(L\)行列の3列目は(14)式のよう求まります。
$$
\begin{eqnarray}
a_{33(3)} &=& u_{33} \\
a_{34(3)} &=& u_{34}
\end{eqnarray} \tag{13}
$$
$$
\begin{eqnarray}
a_{33(3)} = l_{33} u_{33} &\Rightarrow& l_{33} = a_{33(3)} / u_{33} = 1 \\
a_{43(3)} = l_{43} u_{33} &\Rightarrow& l_{43} = a_{43(3)} / u_{33}
\end{eqnarray} \tag{14}
$$
ここで、\(l_3, u_3\)を(15)式のように定義して、
$$
l_3 = (0, 0 , 1 , l_{43}) ^T , u_3 = (0, 0 , u_{33}, u_{34}) \tag{15}
$$
\(A_{(3)} – l_3 u_3 = A_{(4)}\)とすると\(A_{(4)}\)は(16)式のように一つ縮小した形になります。
$$
A_{(4)} =
\left(\begin{array}{ccc|c}
0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 \\ \hline
0 & 0 & 0 & a_{44(4)}
\end{array}\right) \tag{16}
$$
\(A_{(3)} = l_3 u_3 + A_{(4)}\)より、\(A_{(1)} = l_1 u_1 + l_2 u_2 + l_3 u_3 + A_{(4)}\)という関係になります。
4段目
\(A_{(3)}\)から一つ縮小した\(A_{(4)}\)をさらにLU分解を行います。\(A_{(4)}\)の関係から\(LU\)行列も(17)式のようになります。
$$
\left(\begin{array}{ccc|c}
0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 \\ \hline
0 & 0 & 0 & a_{44(4)}
\end{array}\right)=
\left(\begin{array}{ccc|c}
0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 \\ \hline
0 & 0 & 0 & 1
\end{array}\right)
\left(\begin{array}{ccc|c}
0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 \\ \hline
0 & 0 & 0 & u_{44}
\end{array}\right) \tag{17}
$$
(17)式の関係から\(U\)行列の4行目は(18)式、\(L\)行列の4列目は(19)式のよう求まります。
$$
\begin{eqnarray}
a_{44(4)} &=& u_{44}
\end{eqnarray} \tag{18}
$$
$$
\begin{eqnarray}
a_{44(4)} = l_{44} u_{44} &\Rightarrow& l_{44} = a_{44(4)} / u_{44} = 1 \\
\end{eqnarray} \tag{19}
$$
ここで、\(l_4, u_4\)を(20)式のように定義して、
$$
l_4 = (0, 0 , 0 , 1) ^T , u_3 = (0, 0 , 0, u_{44}) \tag{20}
$$
\(A_{(4)} – l_4 u_4 = A_{(5)}\)とすると\(A_{(5)}\)は(21)式のようにゼロ行列になります。
$$
A_{(5)} =
\left(\begin{array}{cccc}
0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0
\end{array}\right) \tag{21}
$$
\(A_{(5)}\)はゼロ行列なので分解できないので、ここでLUへの分解は終了します。
\(A_{(4)} = l_4 u_4\)より、\(A_{(1)} = l_1 u_1 + l_2 u_2 + l_3 u_3 + l_4 u_4\)という関係になります。
LU行列
これまでの計算で \(A_{(1)} = l_1 u_1 + l_2 u_2 + l_3 u_3 + l_4 u_4\)と分解が出来ました。それから\( A_{(1)} = A = LU\)という(1)式の関係がありましたので、(4)式、(10)式、(15)式、(20)式から、L行列とU行列は(22)式のように構成できます。
$$
\begin{eqnarray}
L &=& (l_1 , l_2 , l_3 , l_4 ) \\
U &=& (u_1 , u_2, u_3, u_4 ) ^T
\end{eqnarray} \tag{22}
$$
以上が基本的なA行列をLU行列へ分解するアルゴリズムです。1段目から4段目まで同じ手順で分解していきましたので、アルゴリズムとしてOKですね。
計算上の問題と対策
これまで代数で計算したので現れなかったのですが、\(L\)行列の要素を計算する(3)式、(9)式、(14)式、(19)式は\(U\)行列の対角要素、つまり\(A_{(i)}\)行列の左上の対角要素で割った計算を行っていました。
例えば、2段目の計算で(23)式のように\(A_{(2)}\)行列の左上の要素がゼロになってしまった場合、
$$
\left(\begin{array}{c|ccc}
0 & 0 & 0 & 0 \\ \hline
0 & 0 & a_{23(2)} & a_{24(2)} \\
0 & a_{32(2)} & a_{33(2)} & a_{34(2)} \\
0 & a_{42(2)} & a_{43(2)} & a_{44(2)}
\end{array}\right)=
\left(\begin{array}{c|ccc}
0 & 0 & 0 & 0 \\ \hline
0 & 1 & 0 & 0 \\
0 & l_{32} & 1 & 0 \\
0 & l_{42} & l_{43} & 1
\end{array}\right)
\left(\begin{array}{c|ccc}
0 & 0 & 0 & 0 \\ \hline
0 & u_{22} & u_{23} & u_{24} \\
0 & 0 & u_{33} & u_{34} \\
0 & 0 & 0 & u_{44}
\end{array}\right) \tag{23}
$$
\(u_{22} = 0 \)となり、L行列の要素計算で(24)式のように\(\infty\)となってしまい、計算エラーとなってしまいます。
$$
\begin{eqnarray}
a_{22(2)} = l_{22} u_{22} &\Rightarrow& l_{22} = a_{22(2)} / u_{22} = \infty \\
a_{32(2)} = l_{32} u_{22} &\Rightarrow& l_{32} = a_{32(2)} / u_{22} = \infty \\
a_{42(2)} = l_{42} u_{22} &\Rightarrow& l_{42} = a_{42(2)} / u_{22} = \infty
\end{eqnarray} \tag{24}
$$
この計算エラーを\(Pivot\)という方法で乗り越えます!
ここでようやく半分です。もう少しだけ頑張っていきましょう。
Pivot付きのLU分解
1段目
1段目は普通に計算し、\(l_1, u_1\)が求められたとします。
$$
\left(\begin{array}{cccc}
a_{11(1)} & a_{12 (1) } & a_{13 (1) } & a_{14 (1) } \\
a_{21(1)} & a_{22 (1) } & a_{23 (1) } & a_{24 (1) } \\
a_{31(1)} & a_{32 (1) } & a_{33 (1) } & a_{34 (1) } \\
a_{41(1)} & a_{42 (1) } & a_{43 (1) } & a_{44 (1) }
\end{array}\right) =
\left(\begin{array}{cccc}
1 & 0 & 0 & 0 \\
l_{21} & 1 & 0 & 0 \\
l_{31} & l_{32} & 1 & 0 \\
l_{41} & l_{42} & l_{43} & 1
\end{array}\right)
\left(\begin{array}{cccc}
u_{11} & u_{12} & u_{13} & u_{14} \\
0 & u_{22} & u_{23} & u_{24} \\
0 & 0 & u_{33} & u_{34} \\
0 & 0 & 0 & u_{44}
\end{array}\right)
$$
\(A_{(1)} – 1_l u_1 = A_{(2)}\)の計算で(25)式のように、左上の対角要素がゼロになったとします。
$$
A_{(2)} = \left(\begin{array}{c|ccc}
0 & 0 & 0 & 0 \\ \hline
0 & 0 & a_{23(2)} & a_{24(2)} \\
0 & a_{32(2)} & a_{33(2)} & a_{34(2)} \\
0 & a_{42(2)} & a_{43(2)} & a_{44(2)}
\end{array}\right) \tag{25}
$$
とりあえずこの段階では、\(A_{(1)} = l_1u_1 + A_{(2)}\)です。
2段目
\(A_{(2)}\)の左上の対角要素がゼロとなっていますので、(26)式をそのまま計算すると、Lの要素が \(\infty\) となってしまいます。
$$
\left(\begin{array}{c|ccc}
0 & 0 & 0 & 0 \\ \hline
0 & 0 & a_{23(2)} & a_{24(2)} \\
0 & a_{32(2)} & a_{33(2)} & a_{34(2)} \\
0 & a_{42(2)} & a_{43(2)} & a_{44(2)}
\end{array}\right) =
\left(\begin{array}{c|ccc}
0 & 0 & 0 & 0 \\ \hline
0 & 1 & 0 & 0 \\
0 & l_{32} & 1 & 0 \\
0 & l_{42} & l_{43} & 1
\end{array}\right)
\left(\begin{array}{c|ccc}
0 & 0 & 0 & 0 \\ \hline
0 & u_{22} & u_{23} & u_{24} \\
0 & 0 & u_{33} & u_{34} \\
0 & 0 & 0 & u_{44}
\end{array}\right) \tag{26}
$$
そこでLの要素が\(\infty\)とならないように、値がゼロでない行と入替え(Pivot)を行います。例えば2行目と3行目をPivotするとします。
Pivot(行を入れ替える)方法は例えば2行目と3行目を入れ替える場合、(27)式の\(S_{2,3}\)を\(A_{(1)} = l_1 u_1 + A_{(2)}\)の左側から掛けることで、
$$
S_{2,3} =
\left(\begin{array}{cccc}
1 & 0 & 0 & 0 \\
0 & 0 & 1 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 0 & 1
\end{array}\right) \tag{27}
$$
$$
\begin{eqnarray}
S_{2,3} A_{(1)} &=& S_{2,3} l_1 u_1 + S_{2,3} A_{(2)} \\
&=&
\left(\begin{array}{cccc}
1 & 0 & 0 & 0 \\
0 & 0 & 1 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 0 & 1
\end{array}\right)
\left(\begin{array}{c}
1 \\ l_{21} \\ l_{31} \\ l_{41}
\end{array}\right)
\left(\begin{array}{cccc}
u_{11} & u_{12} & u_{13} & u_{14}
\end{array}\right) \\
&&+
\left(\begin{array}{cccc}
1 & 0 & 0 & 0 \\
0 & 0 & 1 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 0 & 1
\end{array}\right)
\left(\begin{array}{c|ccc}
0 & 0 & 0 & 0 \\ \hline
0 & 0 & a_{23(2)} & a_{24(2)} \\
0 & a_{32(2)} & a_{33(2)} & a_{34(2)} \\
0 & a_{42(2)} & a_{43(2)} & a_{44(2)}
\end{array}\right) \\
&=&
\left(\begin{array}{c}
1 \\ l_{31} \\ l_{21} \\ l_{41}
\end{array}\right)
\left(\begin{array}{cccc}
u_{11} & u_{12} & u_{13} & u_{14}
\end{array}\right)
+
\left(\begin{array}{c|ccc}
0 & 0 & 0 & 0 \\ \hline
0 & a_{32(2)} & a_{33(2)} & a_{34(2)} \\
0 & 0 & a_{23(2)} & a_{24(2)} \\
0 & a_{42(2)} & a_{43(2)} & a_{44(2)}
\end{array}\right) \tag{28}
\end{eqnarray}
$$
(28)式のように、\(A_{(2)}\)の左上の対角要素がゼロではなくなります。このとき、Pivotは関係する全体にかかるので、1段目で計算した\(l_1\)も(28)式のように入れ替わることになります。
このPivotを行った\(S_{2,3} A_{(2)}\)を以下の関係で分解し、\(l_2, u_2\)を計算します。
$$
\left(\begin{array}{c|ccc}
0 & 0 & 0 & 0 \\ \hline
0 & a_{32(2)} & a_{33(2)} & a_{34(2)} \\
0 & 0 & a_{23(2)} & a_{24(2)} \\
0 & a_{42(2)} & a_{43(2)} & a_{44(2)}
\end{array}\right) =
\left(\begin{array}{c|ccc}
0 & 0 & 0 & 0 \\ \hline
0 & 1 & 0 & 0 \\
0 & l_{32} & 1 & 0 \\
0 & l_{42} & l_{43} & 1
\end{array}\right)
\left(\begin{array}{c|ccc}
0 & 0 & 0 & 0 \\ \hline
0 & u_{22} & u_{23} & u_{24} \\
0 & 0 & u_{33} & u_{34} \\
0 & 0 & 0 & u_{44}
\end{array}\right)
$$
すると\(S_{2,3}A_{(1)} = S_{2,3} l_1 u_1 + l_2 u_2 + A_{(3)}\)となります。\(l_2 u_2\)以降は\(S_{2,3}\)が掛かっていませんが、\(l_2, u_2 , A_{(3)}\)を計算するときに既にかかっているので内包していると考えます。
3段目
3段目の計算で\(A_{(3)}\)の左上の対角要素がゼロとなってしまったとします。
$$
A_{(3)} = \left(\begin{array}{cc|cc}
0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 \\ \hline
0 & 0 & 0 & a_{34(3)} \\
0 & 0 & a_{43(3)} & a_{44(3)}
\end{array}\right) \tag{28}
$$
ここで3行目と4行目を入れ替える\(S_{3,4}\)を左から掛けることで、
$$
\begin{eqnarray}
S_{3,4} S_{2,3} A &=& S_{3,4} S_{2,3}l_1 u_1 + S_{3,4} l_2 u_2 +
\left(\begin{array}{cccc}
1 & 0 & 0 & 0 \\
0 &1 & 0 & 0 \\
0 & 0 & 0 & 1 \\
0 & 0 & 1 & 0
\end{array}\right)
\left(\begin{array}{cc|cc}
0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 \\ \hline
0 & 0 & 0 & a_{34(3)} \\
0 & 0 & a_{43(3)} & a_{44(3)}
\end{array}\right) \\
&=& S_{3,4} S_{2,3}l_1 u_1 + S_{3,4} l_2 u_2 +
\left(\begin{array}{cc|cc}
0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 \\ \hline
0 & 0 & a_{43(3)} & a_{44(3)} \\
0 & 0 & 0 & a_{34(3)}
\end{array}\right) \tag{29}
\end{eqnarray}
$$
(29)式のように対角要素がゼロでない\(S_{3,4}A_{(3)}\)となります。また、このとき既に計算した\(l_1, l_2\)もPivotが行われます。
この\(S_{3,4}A_{(3)} \)で以下の関係で分解を行うことで、\(l_3, u_3\)を求めることが出来ます。
$$
\left(\begin{array}{cc|cc}
0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 \\ \hline
0 & 0 & a_{43(3)} & a_{44(3)} \\
0 & 0 & 0 & a_{34(3)}
\end{array}\right) =
\left(\begin{array}{cc|cc}
0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 \\ \hline
0 & 0 & 1 & 0 \\
0 & 0 & l_{43} & 1
\end{array}\right)
\left(\begin{array}{cc|cc}
0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 \\ \hline
0 & 0 & u_{33} & u_{34} \\
0 & 0 & 0 & u_{44}
\end{array}\right)
$$
ここまでの関係は \(S_{3,4} S_{2,3} A = S_{3,4} S_{2,3}l_1 u_1 + S_{3,4} l_2 u_2 + l_3 u_3 + A_{(4)}\)です。
4段目
4段目は(30)式の関係で分解を行い、\(l_4, u_4\)が求まったとします。
$$
\left(\begin{array}{ccc|c}
0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 \\ \hline
0 & 0 & 0 & a_{44(4)}
\end{array}\right)=
\left(\begin{array}{ccc|c}
0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 \\ \hline
0 & 0 & 0 & 1
\end{array}\right)
\left(\begin{array}{ccc|c}
0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 \\ \hline
0 & 0 & 0 & u_{44}
\end{array}\right) \tag{30}
$$
そうするとLUへの分解が終了し、Pivotを行った最終的な式は(31)式のようになります。
$$
S_{3,4}S_{2,4} A = S_{3,4} S_{2,3} l_1 u_1 + S_{3,4} l_2 u_2 + l_3 u_3 + l_4 u_4 \tag{31}
$$
LU分解後の処理
\(P = S_{3,4} S_{2,4}\)とし、\( L= (S_{3,4} S_{2,3} l_1 , S_{3,4} l_2 , l_3, l_4) \)、\(U = (u_1, u_2, u_3, u_4)^T \)とすると、Pivotを行ったLU分解は(32)式のようになります。
$$
PA = L U \tag{32}
$$
入替えの入替えは元に戻るという関係:\(P^2 = I\)より、\(P^{-1} = P\)となるので、(32)式を(33)式になります。
$$
A = P LU \tag{33}
$$
\(A \boldsymbol{x} = \boldsymbol{b}\)の関係があるので、これに(33)式を代入すると(34)式となり、
$$
P L U \boldsymbol{x} = \boldsymbol{b} \tag{34}
$$
(34)式は(35)式となるので、この関係から解\(\boldsymbol{x}\)を求めます。
$$
L U \boldsymbol{x} = P\boldsymbol{b} \tag{35}
$$
プログラムコード – Python
LU行列から方程式を求めるコードも再掲して、LU分解により方程式を求める全体のコードを掲載します。
ここに到達するまですごく長かったですが、プログラムコードは非常にスッキリしています。
Pivotの関数
import numpy as np
# Pivotの影響を受けるA, L P行列をk行を基準に入替え
def Pivot(A, L , k , P):
n = A.shape[0]
n_max = abs(A[k,k])
pivot_n = k
for i in range(k+1, n): # Pivotを行うため、最大の行を探索
if n_max < A[i,k]:
n_max = A[i,k]
pivot_n = i
# Pivot行列の入替え
P_k = np.copy(P[k,:]) # '='だけでは参照渡しになるので copyを使用する
P[k, :] = P[pivot_n, :]
P[pivot_n, :] = P_k
# A行列の入替え
A_k = np.copy(A[k, :]) # '='だけでは参照渡しになるので copyを使用する
A[k, :] = A[pivot_n, :]
A[pivot_n, :] = A_k
# L行列の入替え
L_k = np.copy(L[k, :]) # '='だけでは参照渡しになるので copyを使用する
L[k, :] = L[pivot_n, :]
L[pivot_n, :] = L_k
return A, L , P
LU分解の関数
import numpy as np
# A行列をLU分解
def LU_decomposition(A):
# 配列の作成
L = np.zeros(A.shape)
U = np.zeros(A.shape)
P = np.eye(A.shape[0], A.shape[1])
for i in range(A.shape[0]):
# Pivot実行
A, L, P = Pivot(A, L , i, P)
# L, U 行列の計算
for j in range(i, A.shape[1]):
U[i, j] = A[i, j] # U行列 i 行目を算出
L[j, i] = A[j ,i] / U[i, i] # L行列 i 列目を算出
# 次のA行列を計算
for j in range(A.shape[0]):
for k in range(A.shape[1]):
A[j,k] =A[j,k] - L[j, i] * U[i, k]
return L, U, P
LU行列から方程式を解く関数
import numpy as np
# step 1 計算
def solve_z(L, b):
z = np.zeros(b.shape)
for i in range(z.shape[0]):
r = 0
for j in range(0, i):
r += L[i,j] * z[j]
z[i] = b[i] - r
return z
# step 2 計算
def solve_x(U, z):
x = np.zeros(z.shape)
for i in reversed(range(x.shape[0])):
r = 0
for j in range(i + 1, x.shape[0]):
r += U[i,j] * x[j]
x[i] = (z[i] - r)/U[i,i]
return x
実行
# A行列の定義
A = np.array([[1.0,2.0,3.0],
[2.0,4.0,-9.0],
[5.0,8.0,1.0]])
# A行列をLU行列へ分解、Pivot行列Pも出力
[L, U, P] = LU_decomposition(A)
# b行列の定義
b = np.array([1,2,3])
# b行列をP行列でPivot
pb = np.dot(P, b)
# 方程式の解を求める
z = solve_z(L, pb)
x = solve_x(U, z)
# 求めた解を出力
print(x) # 出力:[-1. 1. 0.]
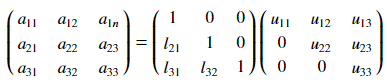
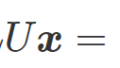
コメント