勾配法やニュートン法など、最適化計算では関数の微分、偏微分が必要になってきます。実装の時に微分、偏微分を手計算してコードを書くと使う関数ごとに異なる実装が必要になりますね。これを避けるために、数値計算で微分を行うことを検討します。
方法は中心差分です。
微分と中心差分
微分の定義は(1)式でしたね。
$$ \frac{d f}{d x} = \lim_{\Delta x \to 0} \frac{f(x + \Delta x) – f(x)}{\Delta x} \tag{1} $$
これを中心差分で表すと(2)式になります。\( \Delta x \)は微小な値です。(1)式の微分ではこの\( \Delta x \)をゼロに近づけていきますが、差分では固定して計算します。
$$ \frac{d f}{d x} =\frac{f(x + \Delta x) – f(x – \Delta x)}{ 2 \Delta x} \tag{2} $$
関数が2変数 \(f (x, y) \)の場合の\(x, y\)それぞれの偏微分の中心差分は、 \(x, y\)への微小距離を\(h\)とおいて
$$
\frac{\partial f(x,y)}{\partial x} =\frac{f(x + h, y) – f(x – h, y)}{ 2 h} \tag{3}
$$
$$
\frac{\partial f(x,y)}{\partial y} =\frac{f(x, y + h) – f(x, y – h)}{ 2 h} \tag{4}
$$
となります。ニュートン法などでヘッセ行列を計算するときに、2階偏微分が必要で、この中心差分は
$$
\frac{\partial^2 f(x,y)}{\partial x^2} =\frac{f(x + h, y) -2f(x, y) + f(x – h, y)}{ h^2} \tag{5}
$$
$$
\frac{\partial^2 f(x,y)}{\partial y^2} =\frac{f(x, y + h) -2f(x, y) + f(x, y – h)}{ h^2} \tag{6}
$$
となります。2階以上の差分については、1階の差分をさらに差分を行うといった計算でも可能です。これは後で実装します。
微分と差分の誤差計算
計算する数式
(7)式の関数を中心差分で計算して、その誤差を確認します。
$$
f(x, y) = -5 (x – 1)^2 – 2(y – 2) ^2 \tag{7}
$$
一階偏微分を計算するとこうですね。
$$
\frac{\partial f(x, y)}{\partial x} = -10(x-1), \frac{\partial f(x, y)}{\partial y} = -4(y-2) \tag{8}
$$
2階偏微分は定数になります。
$$
\frac{\partial^2 f(x, y)}{\partial x^2} = -10, \frac{\partial^2 f(x, y)}{\partial y^2} = -4 \tag{9}
$$
実装 – Python
まず(8),(9)を実装します。関数の実装はlambdaで行います。
# 関数の設定 f = lambda x,y : -5*(x-1)**2 - 2*(y-2)**2 # xで偏微分 df_dx = lambda x, y : -10*(x - 1) # xで2階偏微分 df_dx_dx = lambda x, y: -10 # yで偏微分 df_dy = lambda x, y : -4 * (y -2) # yで2階偏微分 df_dy_dy = lambda x, y: -4
次は(3) – (6)式の中心差分の実装です。
# 微小距離 h = 0.0001 # 1階偏微分 - 中心差分 center_dx = lambda x, y : (f(x + h, y) - f(x - h, y)) / (2*h) center_dy = lambda x, y : (f(x, y + h) - f(x, y - h)) / (2*h) ## 2階偏微分 - 中心差分 center_dx_dx = lambda x, y : (f(x + h, y) - 2 * f(x, y) + f(x - h, y) ) / (h**2) center_dy_dy = lambda x, y : (f(x, y + h) - 2 * f(x, y) + f(x, y - h) ) / (h**2) ## 1階偏微分の中心差分をもう一度1階偏微分の中心差分し、2階偏微分を計算する center_dx_center_dx = lambda x, y: (center_dx (x + h, y) - center_dx(x - h, y)) / (2*h) center_dy_center_dy = lambda x, y: (center_dy (x, y + h) - center_dy(x, y - h)) / (2*h)
誤差計算
\((x, y) = (5, 4) \)として誤差を計算します。
## 計算ポイント x = 5 y = 4 # 1階偏微分の比較 delta_dx = df_dx(x, y) - center_dx(x, y) delta_dy = df_dy(x, y) - center_dy(x, y) print(delta_dx) # 結果 : -9.322320693172514e-11 print(delta_dy) # 結果 : -1.864464138634503e-11
1階偏微分の比較では、その誤差が\( e^{-11} \)となっているので、ほぼ同一であることが確認できました。では2階ではどうでしょうか?
# 2階偏微分の誤差 delta_dxdx = df_dx_dx(x, y) - center_dx_dx(x, y) delta_dydy = df_dy_dy(x, y) - center_dy_dy(x, y) print(delta_dxdx) # 結果 : 2.248489181511104e-06 print(delta_dydy) # 結果 : 3.309614839963615e-07
1階偏微分の計算誤差よりも大きくなっていますが、こちらもほぼ同一といって良さそうですね。
では2階偏微分を1階偏微分の中心差分を2回繰り返して行った場合の誤差はどうでしょうか?
## 1階偏微分をもう一度1階偏微分する方法の誤差 other_delta_dxdx = df_dx_dx(x, y) - center_dx_center_dx(x, y) other_delta_dydy = df_dy_dy(x, y) - center_dy_center_dy(x, y) print(other_delta_dxdx) # 結果 : 1.1686097423080355e-07 print(other_delta_dydy) # 結果 : -2.43098838836886e-08
さきほどの誤差よりも一桁下がっていますね。単純比較だとこちらが良さそうです。
本当は上の誤差の検討は数値精度などを考えないといけませんが、アルゴリズムの確認程度であれば問題ない方法だと思います。勾配法、ニュートン法などの計算では手計算ではなく、この方法で実装して、アルゴリズムを確かめます。
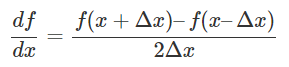

コメント