2変数の場合のテイラー展開を勾配とヘッセ行列の形へ変換できたので、これを多変数に場合に適用してみます。
最後はこの形
先が長いので、前もって結果を示すとこんな感じになります。
$$
f(\boldsymbol{x}) \simeq \bar f + (\nabla \bar f, \boldsymbol{x – \bar x}) + \frac{1}{2}\Bigl( \boldsymbol{x – \bar x}, \bar H ( \boldsymbol{x – \bar x} ) \Bigr)
$$
$$
\boldsymbol{x} =(x_1, \cdots x_n), \boldsymbol{x – \bar x} = (x_1 – \bar x_1 , \cdots , x_n – \bar x_n)^T ,
\\
\nabla \bar f = \left(\begin{array}{c} \partial \bar f / \partial x_1 \\ \vdots \\ \partial \bar f / \partial x_n \end{array} \right) ,
\bar H = \left( \begin{array}{ccc} \partial^2 \bar f / \partial x_1 \partial x_1 & \cdots & \partial^2 \bar f / \partial x_1 \partial x_n \\ \vdots & \ddots & \vdots \\
\partial^2 \bar f / \partial x_n \partial x_1 & \cdots & \partial^2 \bar f / \partial x_n \partial x_n \end{array}\right)
$$
テイラー展開の別表現と2変数の場合の結果と比べてみてくださいね。だんだんこの形が見えてくると思います。
多変数関数のテイラー展開
ではまず多変数関数\(f(x_1, \cdot, x_n) \)のテイラー展開の(1)式から出発しましょう。
$$
f(\bar{x_1} + \Delta x_1, …, \bar{x_n}+\Delta x_n) = \bar f + \sum_{i=1}^{n} \frac{\partial \bar{f}}{\partial x_i} \Delta x_{i} + \frac{1}{2} \sum_{i, j =1}^{n} \frac{\partial ^2 \bar{f}}{\partial x_i \partial x_j} \Delta x_i \Delta x_j + \cdots \tag{1}
$$
1階微分の項の展開
(1)式の1階微分に関する項を展開していくと(2)式になります。
$$
\sum_{i=1}^{n} \frac{\partial \bar{f}}{\partial x_i} \Delta x_{i} = \frac{\partial \bar f}{\partial x_1}\Delta x_1 + \cdots + \frac{\partial \bar f}{\partial x_n}\Delta x_n \tag{2}
$$
ここで、勾配\(\nabla \bar f\)と\(\boldsymbol{\Delta x}\)を以下とすれば、(2)式は(3)式になります。
$$
\nabla \bar f = \left(\begin{array}{c} \partial \bar f / \partial x_1 \\ \vdots \\ \partial \bar f / \partial x_n \end{array} \right), \boldsymbol{\Delta x} = (\Delta x_1, \cdots, \Delta x_n)^T
$$
$$
\sum_{i=1}^{n} \frac{\partial \bar{f}}{\partial x_i} \Delta x_{i} = \bigl( \nabla \bar f, \boldsymbol{\Delta x} \bigr) \tag{3}
$$
2階微分の項の展開
次に(1)式の2階微分に関する項を展開していきます。まず\(i\)を展開していくと(4)式になります。
$$
\sum_{i, j =1}^{n} \frac{\partial ^2 \bar{f}}{\partial x_i \partial x_j} \Delta x_i \Delta x_j = \sum_{j =1}^{n} \frac{\partial ^2 \bar{f}}{\partial x_1 \partial x_j} \Delta x_1 \Delta x_j + \cdots + \sum_{j =1}^{n} \frac{\partial ^2 \bar{f}}{\partial x_n \partial x_j} \Delta x_n \Delta x_j \tag{4}
$$
次に\(j\)に関して展開すると、(5)式になります。
$$
= \frac{\partial ^2 \bar{f}}{\partial x_1 \partial x_1} \Delta x_1 \Delta x_1 + \cdots + \frac{\partial ^2 \bar{f}}{\partial x_1 \partial x_n} \Delta x_1 \Delta x_n +
\\
\vdots
\\
+\frac{\partial ^2 \bar{f}}{\partial x_n \partial x_j} \Delta x_n \Delta x_1 + \cdots + \frac{\partial ^2 \bar{f}}{\partial x_n \partial x_j} \Delta x_n \Delta x_n \tag{5}
$$
これを\(\boldsymbol{\Delta x}\)でまとめいくと、(6)式は(8)式になります。
$$=
\biggl( \frac{\partial ^2 \bar{f}}{\partial x_1 \partial x_1} \Delta x_1 , \cdots , \frac{\partial ^2 \bar{f}}{\partial x_1 \partial x_n} \Delta x_1, \boldsymbol{\Delta x}\biggr) +
\\
\vdots
\\
+\biggl( \frac{\partial ^2 \bar{f}}{\partial x_n \partial x_1} \Delta x_n , \cdots , \frac{\partial ^2 \bar{f}}{\partial x_n \partial x_n} \Delta x_n, \boldsymbol{\Delta x}\biggr) \tag{6}
$$
$$=
\biggl( \Delta x_1 \bigl( \frac{\partial ^2 \bar{f}}{\partial x_1 \partial x_1} , \cdots , \frac{\partial ^2 \bar{f}}{\partial x_1 \partial x_n} \bigr) + \cdots + \Delta x_n \bigl( \frac{\partial ^2 \bar{f}}{\partial x_n \partial x_1} , \cdots, \frac{\partial ^2 \bar{f}}{\partial x_n \partial x_n} \bigr) , \boldsymbol{\Delta x}\biggr)
\tag{7}
$$
$$=
\biggl(
\left(\begin{array}{ccc}
\frac{\partial ^2 \bar{f}}{\partial x_1 \partial x_1} & \cdots & \frac{\partial ^2 \bar{f}}{\partial x_n \partial x_1} \\
\vdots & \ddots & \vdots \\
\frac{\partial ^2 \bar{f}}{\partial x_1 \partial x_n} & \cdots & \frac{\partial ^2 \bar{f}}{\partial x_n \partial x_n}
\end{array}\right) \boldsymbol{\Delta x}
, \boldsymbol{\Delta x}\biggr)
\tag{8}
$$
ここで、対称行列に関する定理 \( (A \boldsymbol{x} , \boldsymbol{y}) = (\boldsymbol{x} , A^T\boldsymbol{y}) \) より(8)式は(9)式になります。
$$=
\biggl(
\boldsymbol{\Delta x}
, \left(\begin{array}{ccc}
\frac{\partial ^2 \bar{f}}{\partial x_1 \partial x_1} & \cdots & \frac{\partial ^2 \bar{f}}{\partial x_1 \partial x_n} \\
\vdots & \ddots & \vdots \\
\frac{\partial ^2 \bar{f}}{\partial x_n \partial x_1} & \cdots & \frac{\partial ^2 \bar{f}}{\partial x_n \partial x_n}
\end{array}\right) \boldsymbol{\Delta x}\biggr)
\tag{9}
$$
ここで\( \bar H \)を以下におくと、(9)式は(10)式になります。
$$
\bar H = \left( \begin{array}{ccc} \partial^2 \bar f / \partial x_1 \partial x_1 & \cdots & \partial^2 \bar f / \partial x_1 \partial x_n \\ \vdots & \ddots & \vdots \\
\partial^2 \bar f / \partial x_n \partial x_1 & \cdots & \partial^2 \bar f / \partial x_n \partial x_n \end{array}\right)
$$
$$
\sum_{i, j =1}^{n} \frac{\partial ^2 \bar{f}}{\partial x_i \partial x_j} \Delta x_i \Delta x_j =
\bigl(
\boldsymbol{\Delta x} , \bar H \boldsymbol{\Delta x}\bigr)
\tag{10}
$$
テイラー展開の式へ代入する
これまでの展開で求められた1階微分の項に関する(3)式と、2階微分の項に関する(10)式をテイラー展開の(1)式へ代入すると、(11)式になります。
$$
f(\bar{x_1} + \Delta x_1, …, \bar{x_n}+\Delta x_n) = \bar f + \bigl(\nabla \bar f, \boldsymbol{\Delta x} \bigr) + \frac{1}{2}\bigl( \boldsymbol{\Delta x}, \bar H \boldsymbol{\Delta x} \bigr) + \cdots \tag{11}
$$
長ったですね、お疲れ様です。

え!最初に示した式と違うじゃない!?
って思われた方、テイラー展開の説明で書いたように、\(x = \bar x + \Delta x \)の関係がありますね。これを(11)式に適用すると(12)式となって最初に示した式になります。
$$
f(\boldsymbol{x}) = \bar f + \bigl(\nabla \bar f, \boldsymbol{x – \bar x} \bigr) + \frac{1}{2}\bigl( (\boldsymbol{x – \bar x}), \bar H (\boldsymbol{x – \bar x}) \bigr) + \cdots \tag{12}
$$
これで、関数のテイラー展開を勾配\(\nabla f\)とヘッセ行列\(H\)で表現することが出来ました。
この多変数のテイラー展開は多変数のニュートン法や共役勾配法で使用したりします。
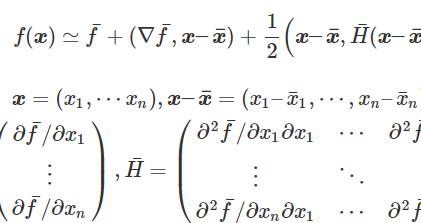
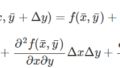
コメント