これなら分かる最適化数学の本には、関数\(f(x)\)のテイラー展開が良く出てきます。近似式という事は式から分かるのですが、実際に何を意味しているかピンとこないですよね。でも図に書いて見たらスッキリ分かりますよ。
テイラー展開を可視化すると
そもそもテイラー展開って何の操作をしているのでしょうか?分かりやすいよう1変数関数で考えてみましょう。
1変数関数のテイラー展開
1変数関数\(f (x)\)を点\(\bar x\) でテイラー展開すると(2)式になります。この式は何を意味しているかと言うと、左辺の”点\(\bar x\)から\(\Delta x\)だけ進んだ点における関数\(f(\bar x + \Delta x)\)の値”は右辺の定数項と微分の組み合わせで表現できるということを意味していますね。
$$
f(\bar x + \Delta x) = f(\bar x) + f^{\prime}(\bar x) \Delta x + \frac{1}{2}f^{\prime \prime}(\bar x)\Delta x^2 + \frac{1}{3!} f^{\prime \prime \prime}(\bar x) \Delta ^3 + \cdots \tag{2}
$$
図で描いて分かるように、(2)式から(3)式のように1階微分の項までを抜き出してみましょう。2解微分以上の項を無視しているので、右辺は左辺の近似式である事に注意しましょう。
$$
f(\bar x + \Delta x) \simeq f(\bar x) + f^{\prime}(\bar x) \Delta x \tag{3}
$$
関数\(f(x)\)を2次の関数として、(3)式を描くとこんな感じです。 \(f^{\prime}(\bar x)\)は関数\(f(x)\)の点\(\bar x\)における傾きなので、図中の青い線です。 傾きなので、 \(f^{\prime}(\bar x) = X_h / \Delta x\) より \(X_h = f^{\prime}(\bar x) \Delta x\)になりますね。よって、 \(f(\bar x + \Delta x)\) は関数\(f(\bar x)\)の値と点\(\bar x\)での1階微分に\(\Delta x\)を掛けたものを足して近似できるという事を示しています。近似なので、左辺の値 \(f(\bar x + \Delta x)\)と右辺の値(赤い線で描かれた緑の〇)はずれていますね。 ちなみに、この関数は2次なので、(3)式に2階微分の項を加えると近似式ではなく、恒等式になります。
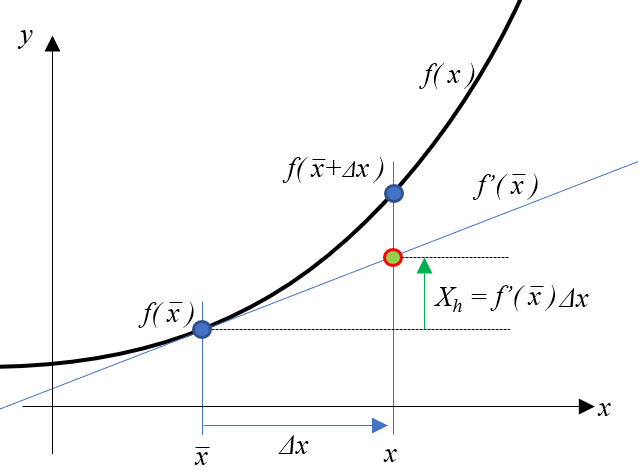
テイラー展開の別表現
それから、図より\( x = \bar x + \Delta x \)という事が分かるので、(2)式の書き換えとして、(4)式、(5)式とも書けることを覚えておきましょう。
$$
f(x) = f(\bar x) + f^{\prime}(\bar x) (x – \bar x) + \frac{1}{2}f^{\prime \prime}(\bar x)(x – \bar x)^2 + \frac{1}{3!} f^{\prime \prime \prime}(\bar x) (x – \bar x) ^3 + \cdots \tag{4}
$$
$$
f(\bar x + \Delta x) = f(\bar x) + f^{\prime}(\bar x) (x – \bar x) + \frac{1}{2}f^{\prime \prime}(\bar x)(x – \bar x)^2 + \frac{1}{3!} f^{\prime \prime \prime}(\bar x) (x – \bar x) ^3 + \cdots \tag{5}
$$
数値計算で可視化してみる
それでは次の関数をテイラー展開して描いてみましょう
$$
f(x) = 0.5 x^3 – 5 x^2 – x -50 \tag{6}
$$
関数の形を描くとこんな感じです。
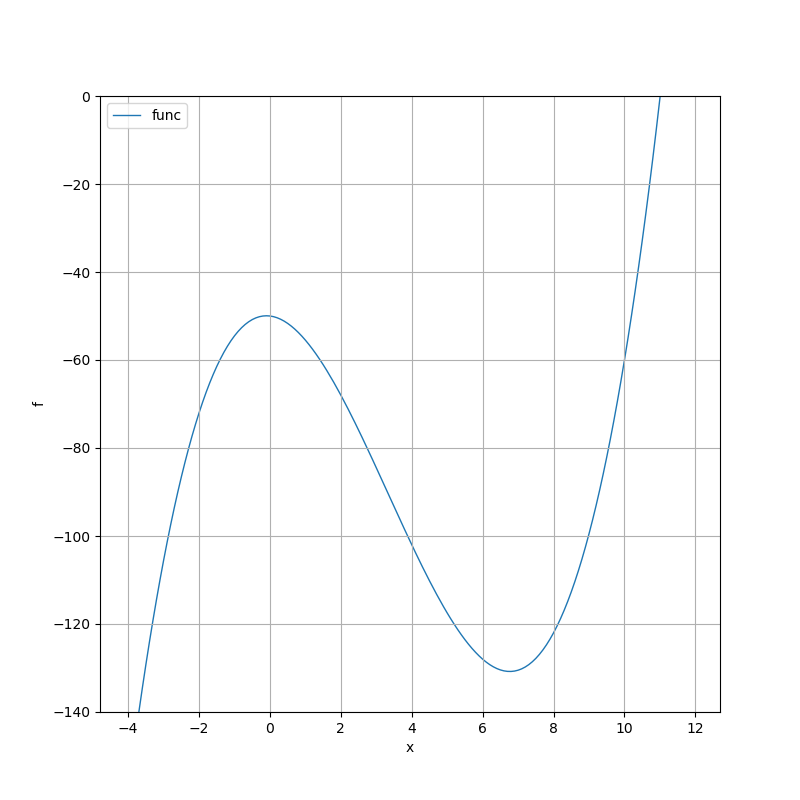
(2)式のテイラー展開を計算するため、それぞれの微分を計算します。関数\(f(x)\)は3次なので、4階微分以上はゼロになると考えると、
$$
f^{\prime} = 1.5 x^2 -10 x – 1 ,
f^{\prime \prime} = 3 x – 10 ,
f^{\prime \prime \prime} = 3
$$
これらを使って、関数\(f(x)\)の(6)式と各オーダーの近似式である(7) 式から(10)式までを一緒にプロットしてみます。\(\bar x = 7 \)で計算しています。
$$
f_0 = f(\bar x) \tag{7}
$$
$$
f_1 = f(\bar x) + f^{\prime}(\bar x)(x – \bar x) \tag{8}
$$
$$
f_2 = f(\bar x) + f^{\prime}(\bar x)(x – \bar x) + \frac{1}{2} f^{\prime \prime}(\bar x)(x – \bar x)^2 \tag{9}
$$
$$
f_3 = f(\bar x) + f^{\prime}(\bar x)(x – \bar x) + \frac{1}{2} f^{\prime \prime}(\bar x)(x – \bar x)^2 + \frac{1}{3!} f^{\prime \prime \prime}(\bar x)(x – \bar x)^3 \tag{10}
$$
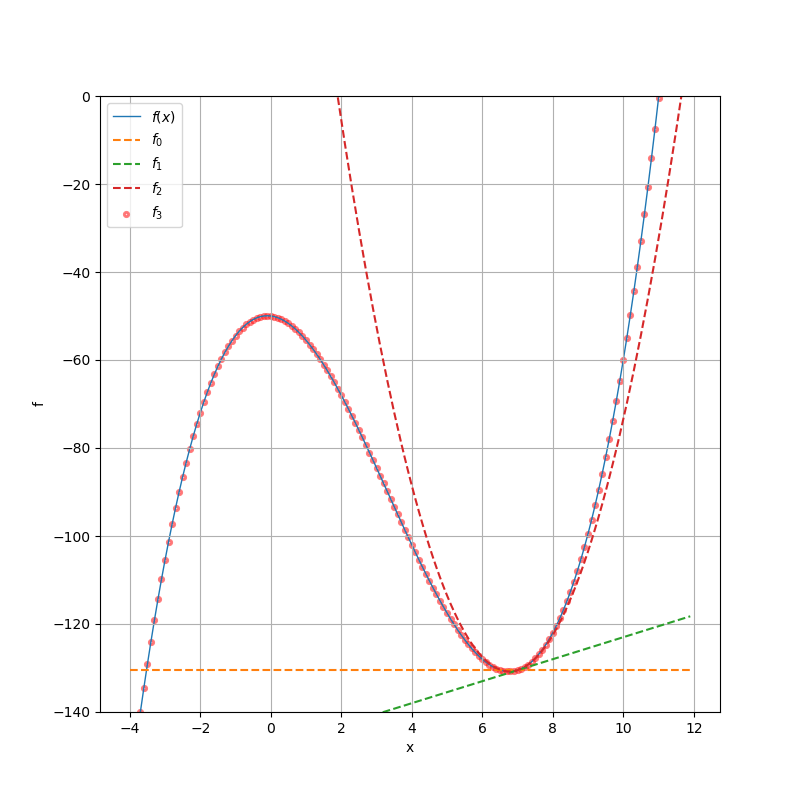
3次項までを近似した\(f_3\)は、元の関数\(f(x)\)と一致していますね。この図をもう少し\(\bar x\)に近づけてみましょう。

\( x = 7\)の位置で、\(f(x) = f_0 = f_1 = f_2 = f_3\)となっている事が分かりますね。それから、\(x = 7\)から離れるにつれて、\(f_0\)から\(f_2\)までは\(f(x)\)からずれていきます。オーダーが少ないほどずれが大きいです。
以上の結果から、考えられることは
・テイラー展開による近似式は、元の関数\(f(x)\)と同じオーダーまで考慮すると、元の関数と一致する(上記の場合は、\(f(x) = f_3 )\)
・テイラー展開を行う点\(\bar x\)の近くであれば、元の関数と同じオーダーまで考慮した近似式でなくても、それなりに近似ができる(上記の場合は、\(f(x) \simeq f_0 \simeq f_1 \simeq f_2) \)
関数の最適化を行うときには、このテイラー展開をもとに式変形を行うことがあります。ニュートン法や共役勾配法を考える場合に、勾配とヘッセ行列の表現式で考えますが、この表現式はテイラー展開をもとにしたものだったりします。

コメント