バウムガルテの安定化法

Multi Body Dynamicsの動力学計算を行うときに、フィードバック制御の形が存在している、というお話です。

拘束条件を伴う順運動学の微分代数方程式
問題点
誤差修正方法(バウムガルテの安定化法)
フィードバックの効果
バウムガルテの安定化法を加えた微分代数方程式

拘束条件を伴う順運動学の微分代数方程式

Multi Body Dynamicsでは下のような代数方程式を用いて動力学の計算を行います。

$$
\begin{equation}
\begin{bmatrix}
\boldsymbol{M} & \boldsymbol{C}_q^T \\
\boldsymbol{C}_q & \boldsymbol{0}
\end{bmatrix}
\begin{bmatrix}
\boldsymbol{\ddot{q}} \\ \boldsymbol{\lambda}
\end{bmatrix}=
\begin{bmatrix}
\boldsymbol{Q} \\ \gamma
\end{bmatrix}
\end{equation}
$$

一行目の式が運動方程式で、2列目の式が加速度レベルの拘束条件式を示しています。

行列を解くことで、
$$
\begin{equation}
\begin{bmatrix}
\boldsymbol{\ddot{q}} \\ \boldsymbol{\lambda}
\end{bmatrix}
\end{equation}
$$

が求められるので、

$$
\boldsymbol{y} =
\begin{bmatrix}
\boldsymbol{q} \\
\boldsymbol{\dot{q}}
\end{bmatrix} \, ,\quad
\boldsymbol{\dot{y}} =
\begin{bmatrix}
\boldsymbol{\dot{q}} \\
\boldsymbol{\ddot{q}}
\end{bmatrix}
$$

のように定義すれば、

$$
\boldsymbol{\dot{y}} =\boldsymbol{F} ( \boldsymbol{y}, t)
$$

と常微分方程式を構成すれば、少し先の時間の位置と速度を数値積分で求めることが出来ます。

この部分をもう少し説明すると、一番初めの行列は $\boldsymbol{q}(t), \boldsymbol{\dot{q}}(t)$ の関数となっていて、次のように計算した後、

$$
\begin{bmatrix}
\boldsymbol{\ddot{q}} \\ \boldsymbol{\lambda}
\end{bmatrix}=
\begin{equation}
\begin{bmatrix}
\boldsymbol{M} & \boldsymbol{C}_q^T \\
\boldsymbol{C}_q & \boldsymbol{0}
\end{bmatrix}^{-1}
\begin{bmatrix}
\boldsymbol{Q} \\ \gamma
\end{bmatrix}
\end{equation}
$$

$\boldsymbol{q}(t), \boldsymbol{\dot{q}}(t)$ に関して抽出すると

$$
\begin{equation}
\begin{bmatrix}
\boldsymbol{\dot{q}} \\ \boldsymbol{\ddot{q}}
\end{bmatrix}
\end{equation} =
\boldsymbol{F} \left( \begin{bmatrix}\boldsymbol{q} \\ \boldsymbol{\dot{q}} \end{bmatrix}, t \right)
$$

このように構成出来ます。

この構成でルンゲクッタ・ギル法などを適用すれば、少し先の $y(t + \Delta t)$ を計算することが出来る、という事です。

問題点

$\boldsymbol{C}_q \boldsymbol{\ddot{q}} = \boldsymbol{\gamma}$ は拘束 $\boldsymbol{C}$ を2回時間微分した式です。

拘束条件なので、拘束$\boldsymbol{C} = 0$ であり、2階微分した式も $\boldsymbol{\ddot{C}} = \boldsymbol{C}_q \boldsymbol{\ddot{q}} – \boldsymbol{\gamma} = \boldsymbol{0}$ であることが求められます。

上式は $\boldsymbol{\ddot{q}, \, \dot{q} , \, q}$ に関連していて、数値計算を行う過程で何らかの誤差が発生し、 ” $= \boldsymbol{0}$ “にはならない可能性があります。

計算誤差は計算の都度で発生するとすると $\boldsymbol{\ddot{C}} = d(t)$ とインパルス状の外乱はとして捉えれるので、 $d(t) = \delta(t)$とデルタ関数で表し

$\int_0^\infty \delta(t) dt = 1$ であることを踏まえ、時間ゼロからずっと積算していくと、

$$
\begin{align}
\boldsymbol{\dot{C}} &= \int_0^\infty \boldsymbol{\ddot{C}} dt = \int_0^\infty \delta{t} dt = 1 \\
\boldsymbol{{C}} &= \int_0^\infty \boldsymbol{\dot{C}} dt = \int_0^\infty dt = \left[ t \right]_0^\infty
\end{align}
$$

上記のように、2階微分の拘束条件 $\boldsymbol{\ddot{C}}$ の計算誤差がインパルス状の誤差であっても、拘束 $\boldsymbol{C}$ の誤差は無限大に増えていくことが分かります。

これにより、例えばジョイントの拘束を行っていても、数値計算誤差によりそのジョイントが時間とともに構成されなくなります(ずれていきます)。

誤差修正方法(バウムガルテの安定化法)

$\boldsymbol{\ddot{C}} = d(t)$ をラプラス変換すると、

$$
\mathcal{L}[\boldsymbol{\ddot{C}}] = s^2 C(s) \ , \quad \mathcal{L}[d(t)] = D(s)
$$

より、$D(s)$ から $C(s)$ までの伝達関数は次のようになります。

$$
\frac{C(s)}{D(s)} = \frac{1}{s^2}
$$

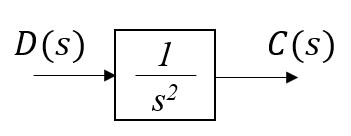
これに次のようなフィードバックを施すことをバウムガルテの安定化法と言います。

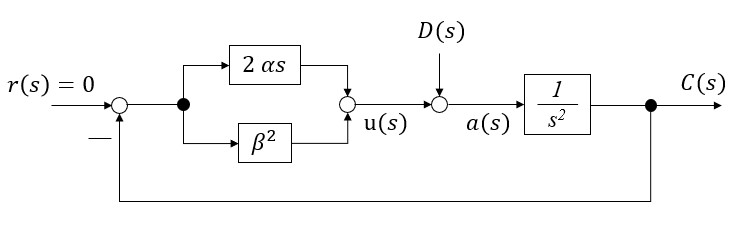
$r(s)$ は目標値でこれをゼロに設定しています。また、 $\alpha, \beta >0$ です。

フィードバックの効果

この構造で $D(s)$ から $C(s)$ までの伝達関数を求めます。

$$
\begin{align}
a(s) &= D(s) – (2 \alpha s + \beta^2) C(s) \\
C(s) &= \frac{1}{s^2} a(s) \\
C(s) &= \frac{1}{s^2} \left( D(s) – (2 \alpha s + \beta^2) C(s) \right) \\
D(s) &= \left( s^2 + 2 \alpha s + \beta^2 \right) C(s) \\
\frac{C(s)}{D(s)} &= \frac{1}{s^2 + 2 \alpha s + \beta^2}
\end{align}
$$

分母に2次方程式の解の公式で適用すると、次のようになります。

$$
\frac{C(s)}{D(s)} = \frac{1}{\left(s + \alpha – \sqrt{\alpha^2 – \beta^2} \right)\left(s + \alpha + \sqrt{\alpha^2 – \beta^2} \right)}
$$

今この式は$s$ 領域なので、時間領域へ戻して $d(t)$ から $C(t)$ への応答を求めるとどうなるか分かります。

上記の式の逆ラプラス変換を行うため、3つの場合分けがあります。

case1 : $\alpha^2 – \beta^2 < 0$

この場合、式は

$$
\begin{align}
\frac{C(s)}{D(s)} &= \frac{1}{\left(s + \alpha – i \sqrt{\beta^2 – \alpha^2} \right)\left(s + \alpha + i\sqrt{\beta^2 – \alpha^2} \right)} \\
&= \frac{1}{(s+\alpha)^2 – \left( i \sqrt{\beta^2 – \alpha^2} \right) ^2} \\
&= \frac{1}{(s+\alpha)^2 + \left( \sqrt{\beta^2 – \alpha^2} \right) ^2} \\
\end{align}
$$

となって、次のラプラス変換の関係より

$$
\mathcal{L} \left[ e^{-a t} \sin \omega t\right] = \frac{\omega}{(s+a)^2 + \omega^2}
$$

$$
C(t) = \frac{1}{\sqrt{\beta^2 – \alpha^2}} e^{-\alpha t} \sin \left(\sqrt{\beta^2 – \alpha^2} t \right) d(t)
$$

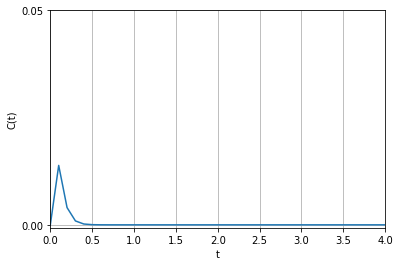
$\alpha > 0 $ であり、 $e^{- \alpha t}$ があるため、ある時間のインパルス状の誤差 $d(t)$ の影響が時間とともにゼロに収束することが分かります。

$d(t) = 1$として応答を計算させると次のようになります。$\alpha = 10 , \, \beta=20 $ です。

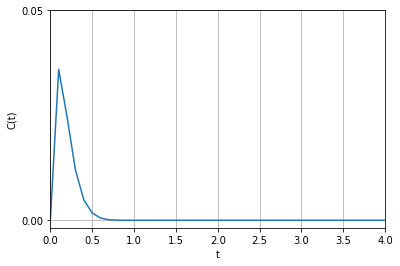
case2 : $\alpha ^2 – \beta^2 = 0$

この場合、式は

$$
\begin{align}
\frac{C(s)}{D(s)} = \frac{1}{\left(s + \alpha \right)^2} \
\end{align}
$$

となって、次のラプラス変換の関係より

$$
\mathcal{L} \left[ t e^{-a t} \right] = \frac{1}{(s+a)^2}
$$

$$
C(t) = t e^{-\alpha t} d(t)
$$

case1と同じく、 $d(t) = 1$として計算させると次のような収束を行います。 $\alpha = 20$です。

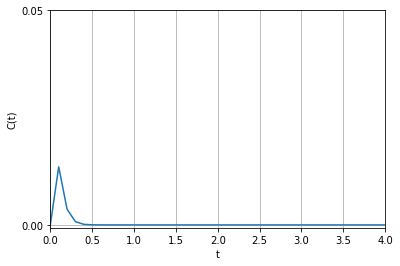
case3 : $\alpha^2 – \beta^2 > 0$

この場合、式は

$$
\begin{align}
\frac{C(s)}{D(s)} = \frac{1}{\left(s + \alpha – \sqrt{\alpha^2 – \beta^2} \right)\left(s + \alpha + \sqrt{\alpha^2 – \beta^2} \right)} \end{align}
$$

この式を次のように

$$
\begin{align}
\frac{1}{\left(s + \alpha – \sqrt{\alpha^2 – \beta^2} \right)\left(s + \alpha + \sqrt{\alpha^2 – \beta^2} \right)}
&= \frac{A}{ s + \alpha – \sqrt{\alpha^2 – \beta^2} } + \frac{B}{s + \alpha + \sqrt{\alpha^2 – \beta^2}} \\
1 &= A \left( s + \alpha + \sqrt{\alpha^2 – \beta^2} \right) + B \left(s + \alpha – \sqrt{\alpha^2 – \beta^2} \right) \\
1 &= (A + B) s + (A+B) \alpha + (A – B) \sqrt{\alpha^2 – \beta^2}
\end{align}
$$

左辺 = 右辺の関係より、$s$ と $\alpha$ の数をゼロとすれば恒等式が成り立つので、

$$
\begin{align}
A+B &= 0 \\
(A-B) \sqrt{\alpha^2 – \beta^2} &= 1
\end{align}
$$

ここから $A,B$ を求めると

$$
\begin{align}
\begin{bmatrix}
1 & 1 \\
\sqrt{\alpha^2 – \beta^2} & – \sqrt{\alpha^2 – \beta^2}
\end{bmatrix}
\begin{bmatrix}
A \\ B
\end{bmatrix} &=
\begin{bmatrix}
0 \\ 1
\end{bmatrix} \\
\begin{bmatrix}
A \\ B
\end{bmatrix} &=
-\frac{1}{2 \, \sqrt{\alpha^2 – \beta^2}}
\begin{bmatrix}
\sqrt{\alpha^2 – \beta^2} & -1 \\ \sqrt{\alpha^2 – \beta^2} & 1
\end{bmatrix}
\begin{bmatrix}
0 \\ 1
\end{bmatrix} \\
&=
\frac{1}{2 \, \sqrt{\alpha^2 – \beta^2}}
\begin{bmatrix}
1 \\ -1
\end{bmatrix} \\
\end{align}
$$

よって伝達関数 $C(s) / D(s)$ は

$$
\frac{C(s)}{D(s)} = \frac{1}{2 \sqrt {\alpha^2 – \beta^2}}\frac{1} { s + \alpha – \sqrt{\alpha^2 – \beta^2} } -\frac{1}{2 \sqrt {\alpha^2 – \beta^2}} \frac{B}{s + \alpha + \sqrt{\alpha^2 – \beta^2}} \
$$

ここで、次のラプラス変換の関係より

$$
\mathcal{L} \left[ e^{-a t} \right] = \frac{1}{(s+a)}
$$

$$
C(t) = \left( \frac{1}{2\sqrt {\alpha^2 – \beta^2}} e^{- \left(\alpha – \sqrt {\alpha^2 – \beta^2}\right) t} – \frac{1}{2\sqrt {\alpha^2 – \beta^2}} e^{- \left(\alpha + \sqrt {\alpha^2 – \beta^2}\right) t} \right) \ d(t)
$$

case1と同じく $d(t) = 1$として応答を計算すると、次のような収束をします。$\alpha = 20, \beta=10$です。