”これなら分かる最適化数学, 金谷健一 “を学習中です。共役な方向とはなんだろうという事が図形で分かったので、実際に共役勾配法を実装してみます。ちなみに、共役の読み方は”キョウエキ”ではなく”キョウヤク”ですよ。
全体的な流れとアルゴリズム
関数\(f(\boldsymbol{x})\)に対して、以下のステップでその関数の極値を計算します。
- Step 1: 初期値\(\boldsymbol{x^0}\)と探索方向\(\boldsymbol{m^0}\)を設定
- Step 2: \(\boldsymbol{\bar x} = \boldsymbol{x^0}\)、\(\boldsymbol{\bar m} = \boldsymbol{m^0}\)とする
- Step 3: \( f(\boldsymbol{\bar x} + \beta \boldsymbol{\bar m}) \)が最小となるスカラー\(\beta\)を計算する
- Step 4: 近似解 \(\boldsymbol{x} = \boldsymbol{\bar x} + \beta\boldsymbol{\bar m} \)を計算する
- Step 5: 次の探索方向 \(\boldsymbol{m^{k+1}}\)を共役勾配な関係から決める
- Step 6: \(|\boldsymbol{x – \bar x}| < \sigma \)になるまで、 \( \boldsymbol{\bar x} = \boldsymbol{x} \)、\(\boldsymbol{\bar m} = \boldsymbol{m^{k+1}} \)として Step 3から Step 6を繰り返す
Step 5以外は勾配法と同じですね。
Step 5の共役勾配な方向は次のような関係から求めます。
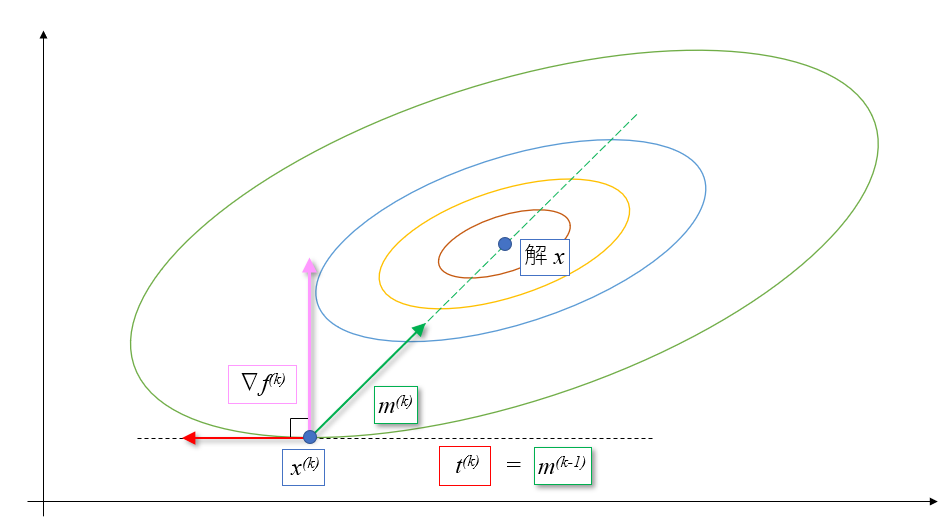
\(k\)回目の点\(\boldsymbol{x^{(k)}}\)では、共役勾配な関係より(1)式の関係があります。\(H^{(k)}\)は点\(\boldsymbol{x^{(k)}}\)でのヘッセ行列です。
$$
\bigl( \boldsymbol{t^{(k)}}, H^{(k)} \boldsymbol{m^{(k)}} \bigr) = 0 \tag{1}
$$
そして上の図の関係から共役勾配な方向 \(\boldsymbol{m^{(k)}}\)は、スカラー値\(\alpha\)を使い、勾配な方向(ベクトル)\(\nabla f^{(k)}\)と接線方向(ベクトル) \(\boldsymbol{t^{(k)}}\)を足し合わせることと計算できます。
$$
\boldsymbol{m^{(k)}} = \nabla f^{(k)} + \alpha \boldsymbol{t^{(k)}} \tag{2}
$$
(1), (2)式では、\(\boldsymbol{m^{(k)}}と\alpha\)が未知数なので、(2)式を(1)式にして\(\boldsymbol{m^{(k)}}\)を消去して\(\alpha\)を計算します。
$$
\bigl( \boldsymbol{t^{(k)}}, H^{(k)} (\nabla f^{(k)} + \alpha \boldsymbol{t^{(k)} }) \bigr) = 0 \tag{3}
$$
(3)式を展開すると(4)式になるので、
$$
\bigl( \boldsymbol{t^{(k)}}, H^{(k)} \nabla f^{(k)} \bigr) + \alpha\bigl( \boldsymbol{t^{(k)}}, H^{(k)} \boldsymbol{t^{(k) }}) \bigr) = 0 \tag{4}
$$
\(\alpha\)を(5)式で計算できます。
$$
\alpha = – \frac { \bigl( \boldsymbol{t^{(k)}}, H^{(k)} \nabla f^{(k)} \bigr) } { \bigl( \boldsymbol{t^{(k)}}, H^{(k)} \boldsymbol{t^{(k) }}) \bigr) } \tag{5}
$$
ここで、\(\boldsymbol{t^{(k)}}\)はひとつ前の共役勾配な方向\(\boldsymbol{m^{(k-1)}}\)であるということを考えると、(5)式は(6)式になります。
$$
\alpha = – \frac{ \bigl( \boldsymbol{m^{(k-1)}}, H^{(k)} \nabla f^{(k)} \bigr) } { \bigl( \boldsymbol{m^{(k-1)}}, H^{(k)} \boldsymbol{m^{(k-1) }}) \bigr) } \tag{6}
$$
これより、Step 5の共役勾配な方向は(2)式と(3)式から求めることができます。
共役勾配法を数値計算
では実際に関数に共役勾配法のアルゴリズムを適用して極値を探してみましょう。共役勾配な方向での探索には、最大値を探す勾配法を使用します。
単純な楕円関数
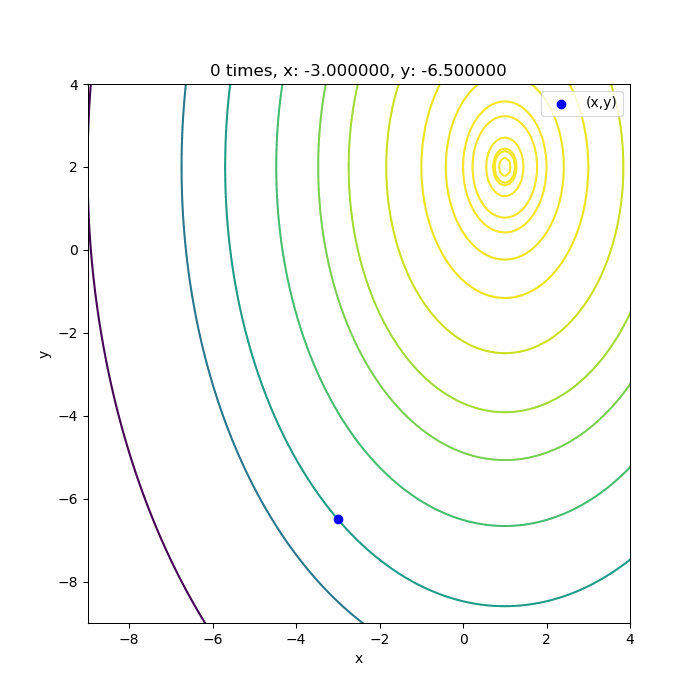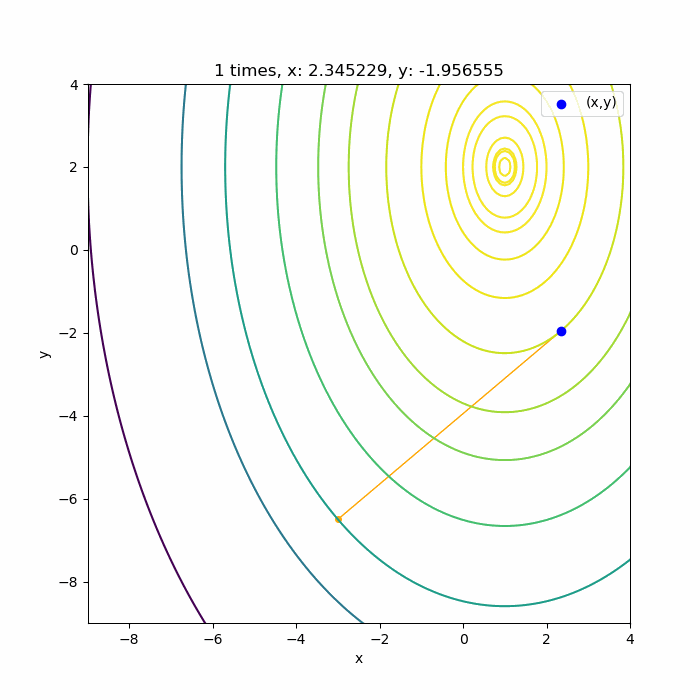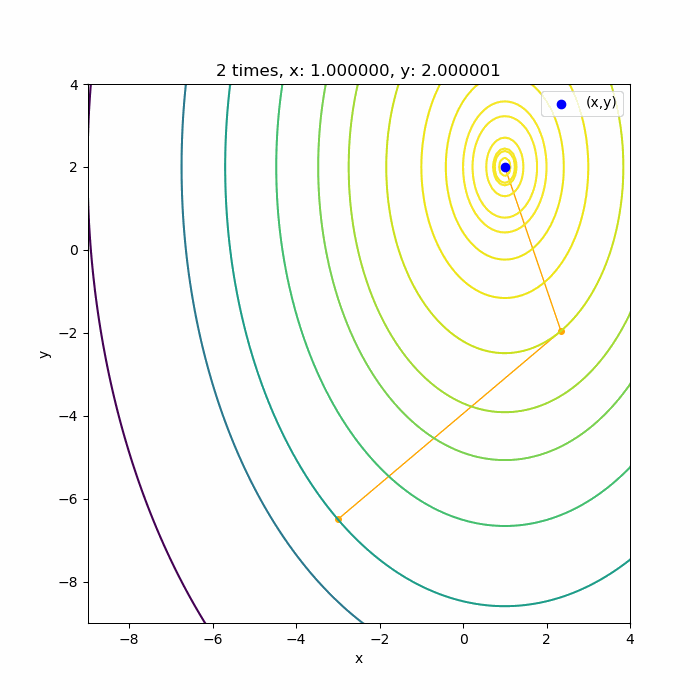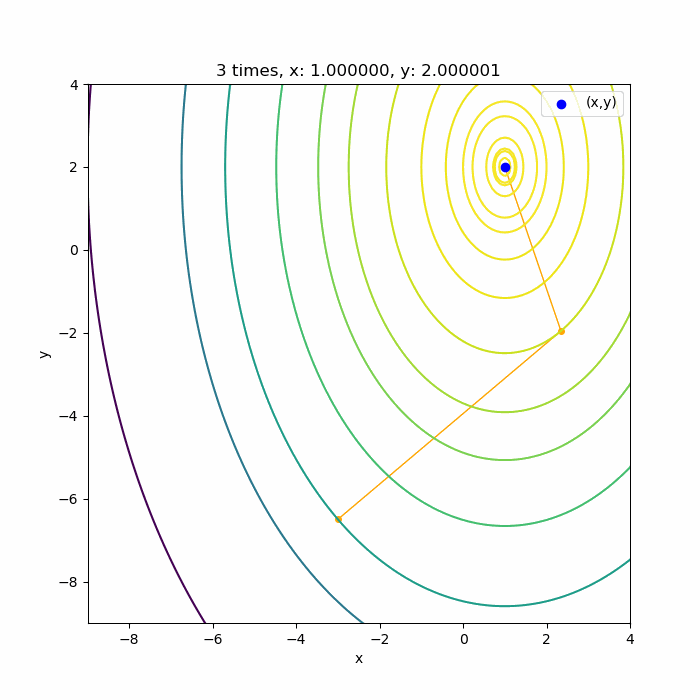
\(f(x,y) = -5(x-1)^2 -2 (y-2)^2\)で共役勾配法のアルゴリズムを適用するとこんな感じです。
勾配法を多変数関数に適用したときと同じ関数で、かつ同じ初期値\((-3, -6.5)\)から始めています。勾配法がガタガタしながら収束していたのと比べると、とても素早く収束していることが分かりますね。
理論的には2回の計算で収束するみたいですが、今回は勾配とヘッセ行列の偏微分を中心差分で求めていること、それから最大値探索に使用している勾配法は数値計算で最大値を探しているため、これらの誤差が乗って3回で収束するのかな、と思います。
歪んだ楕円関数
次は \(f(x,y) = -x^2 + xy – y^2 + x + y\) に適用してみます。
こんな感じです。
多少歪んでいても2次関数なので、すんなり収束してくれますね。

3次関数
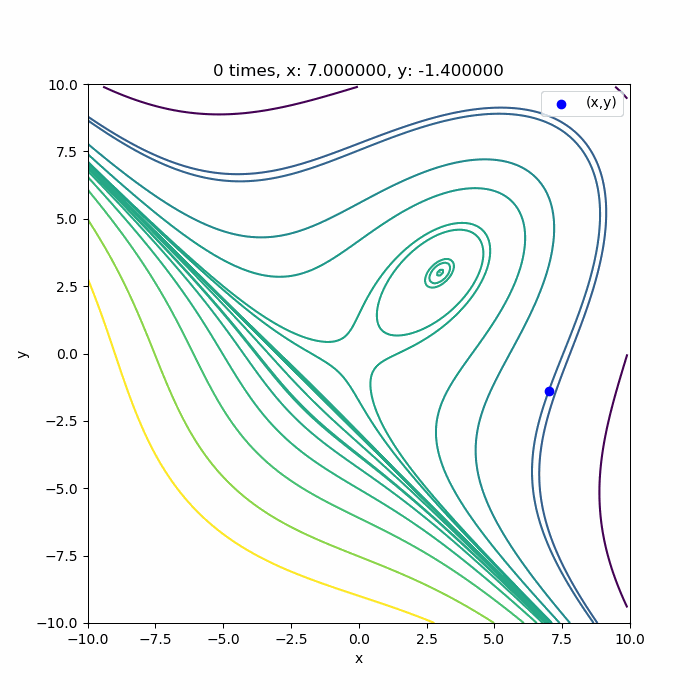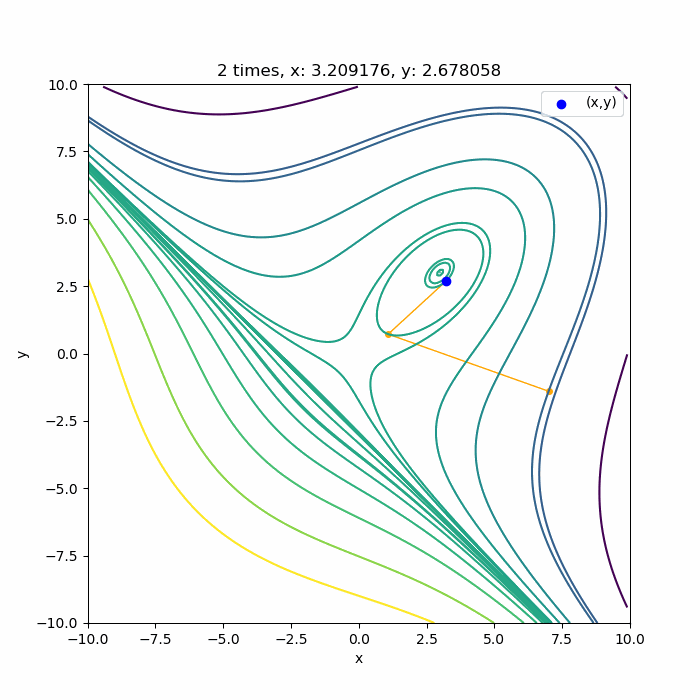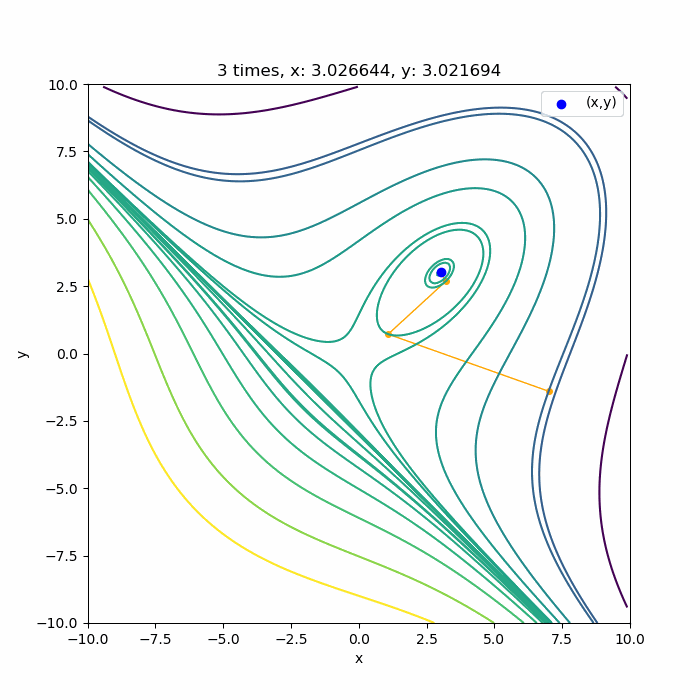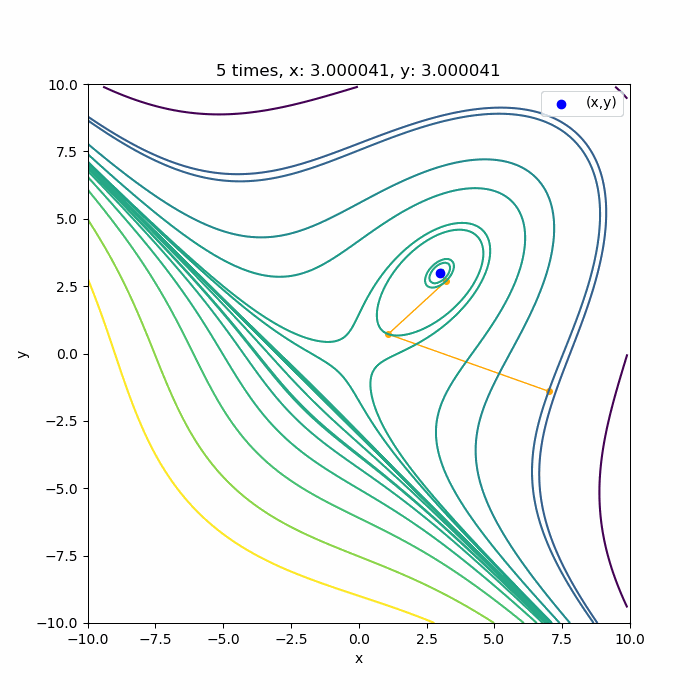
次は多変数のニュートン法でも使用した3次関数のz方向を反転した関数 \( f(x,y) = -(x^3 + y^3 -9 xy + 27) \)に適用してみます。

なぜ反転したかって??
ニュートン法で使用した関数 \( f(x,y) = (x^3 + y^3 -9 xy + 27) \) の形を見てもらうと、赤い領域が下に凸な形で、青い領域はずっと降る形をしていることが分かります。今回の共役勾配法は、直線探索で最大値を見つける勾配法を使用しているので、上に凸な形でないと極値が求まりません。という事で、 関数を\( f(x,y) = -(x^3 + y^3 -9 xy + 27) \)のように反転すると、赤い領域が上に凸な形になって極値を求めることが出来るようになります。これが反転の理由です。言い換えると、凸でない青い領域では、今回の共役勾配法で極値を求めることが出来ません。
結果はこんな感じです。3次関数なので、3回目の収束でほぼ極値に到達していますね。ほぼ理論通りかと思います。
初期値を変えても
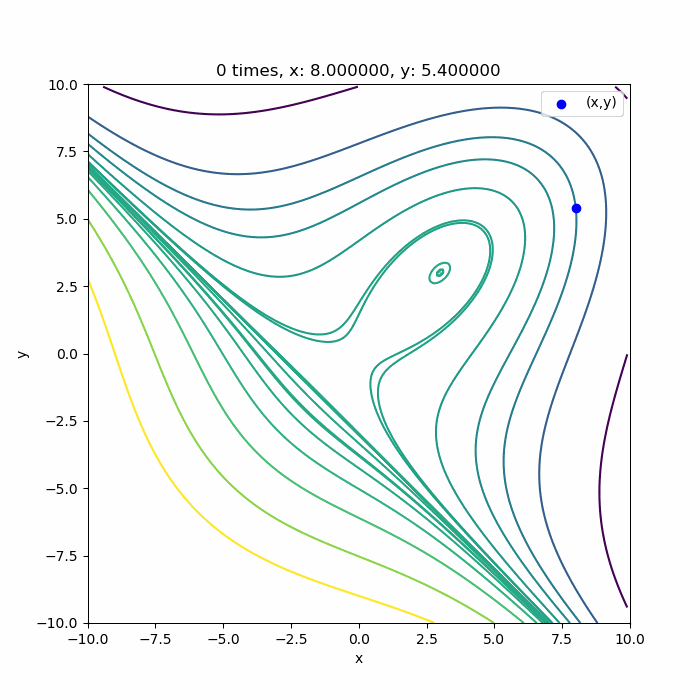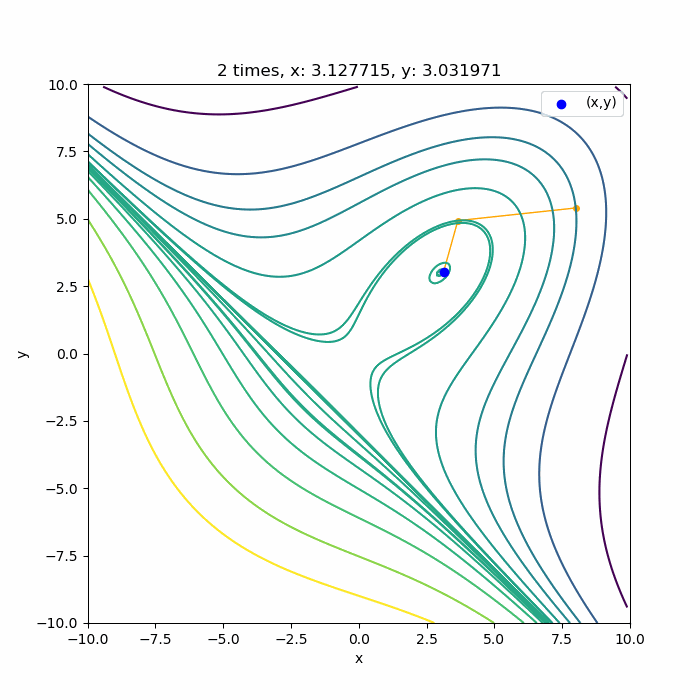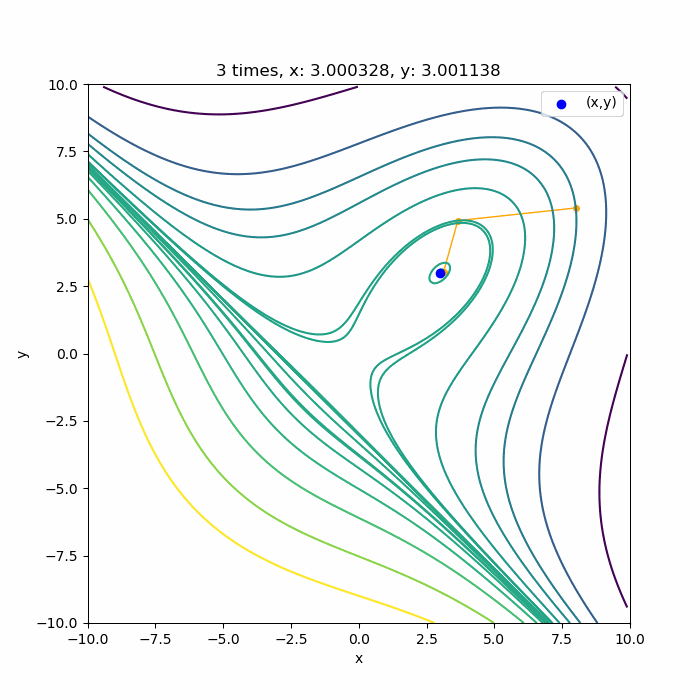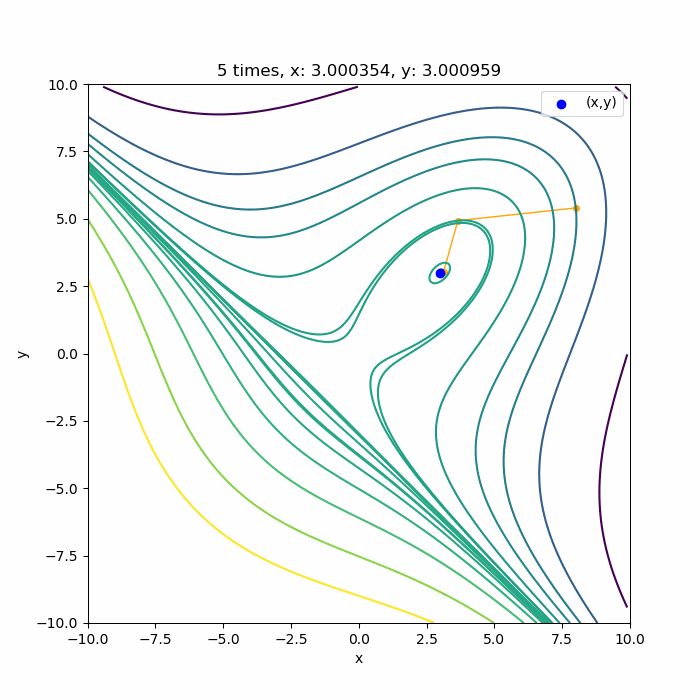
上に凸な領域であれば
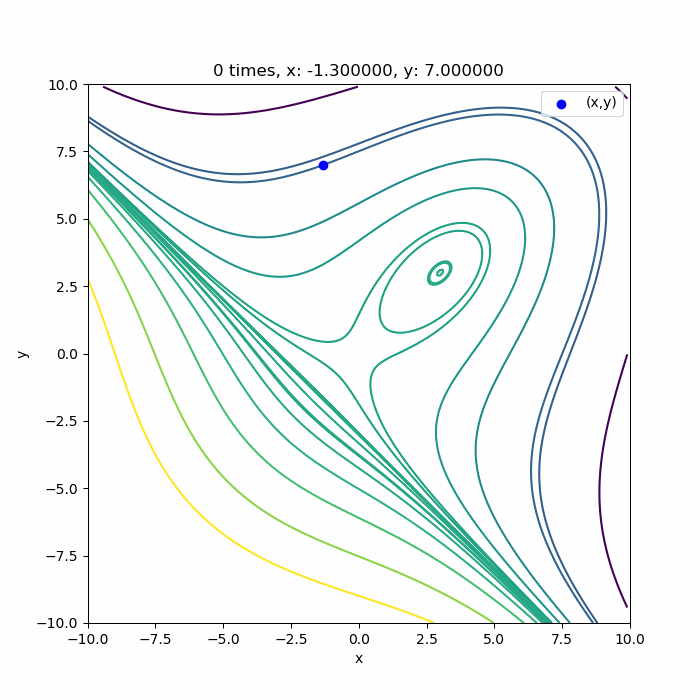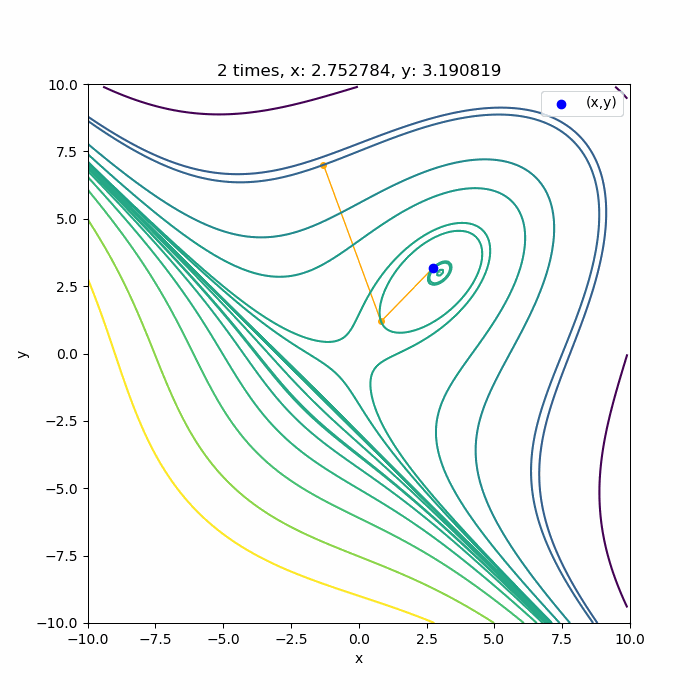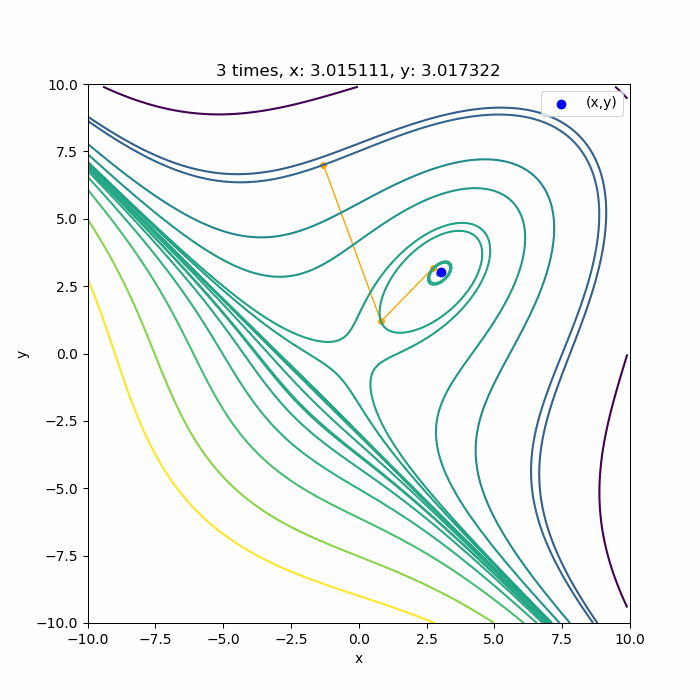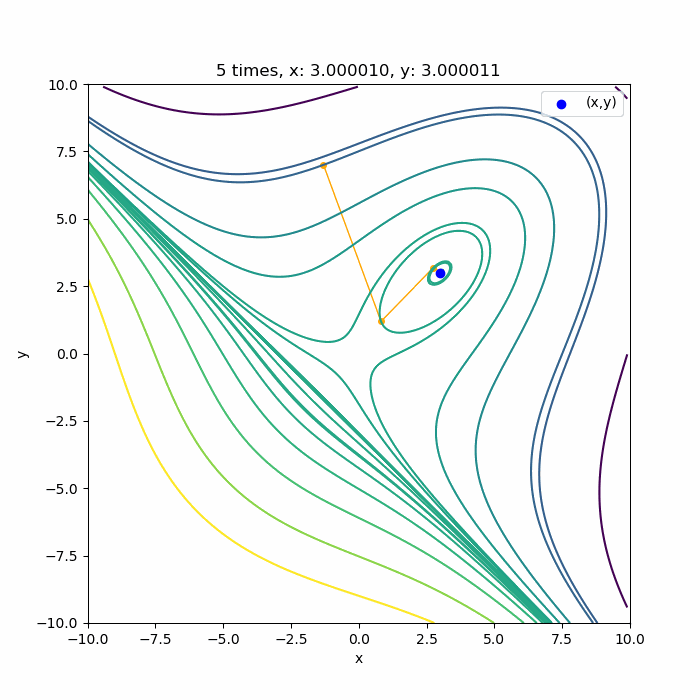
こんな感じで、ちゃんと3回目で極値付近に収束していますね。収束できるのは、0回目の探索方向が上に凸な領域の方向に向いている場合です。
そうでない場合は、次の結果のようにどこかに発散してしまいます。
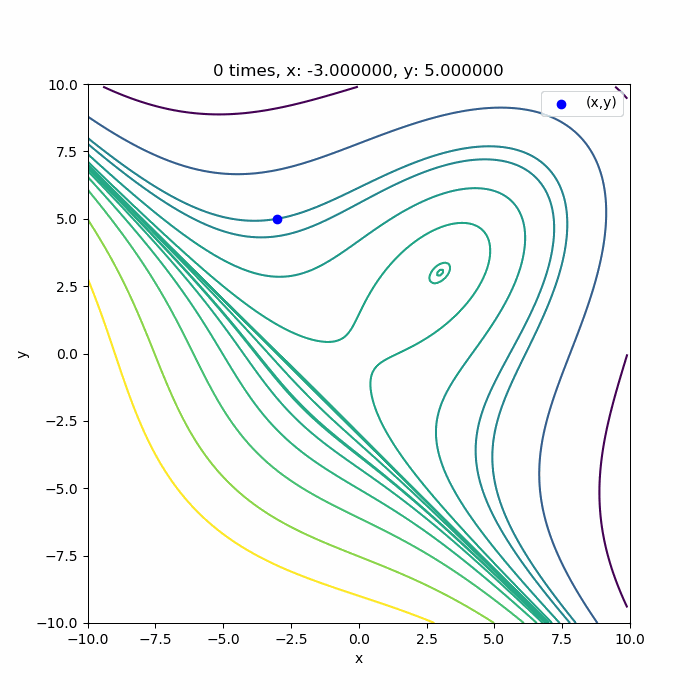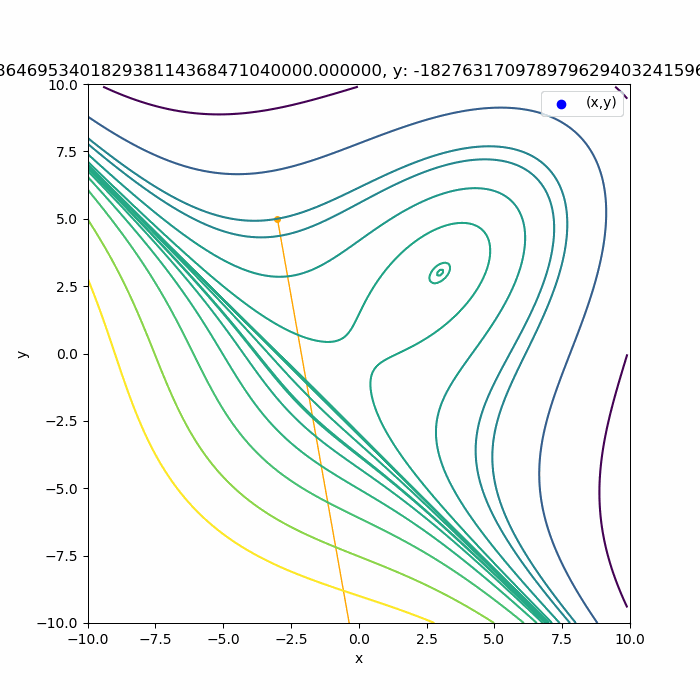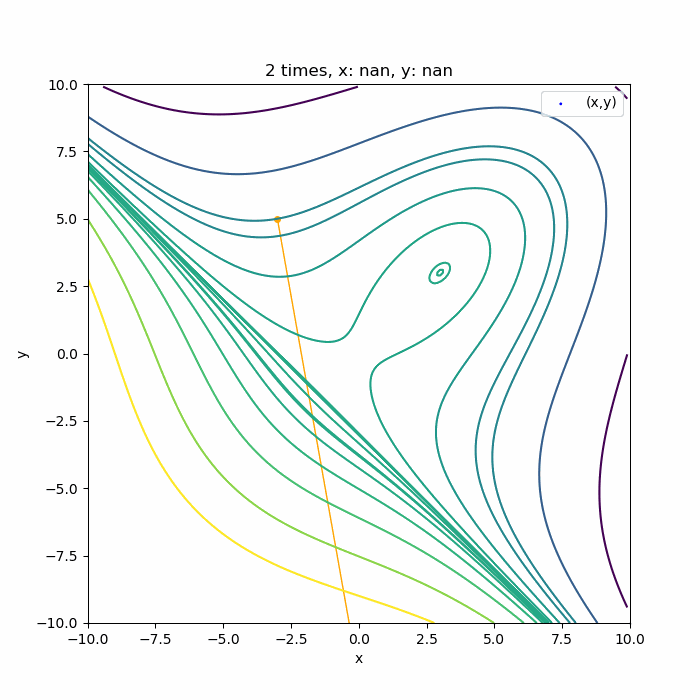
この関数に使っていいのかな?初期値はここで大丈夫かな?というところに注意ですね。
4次関数
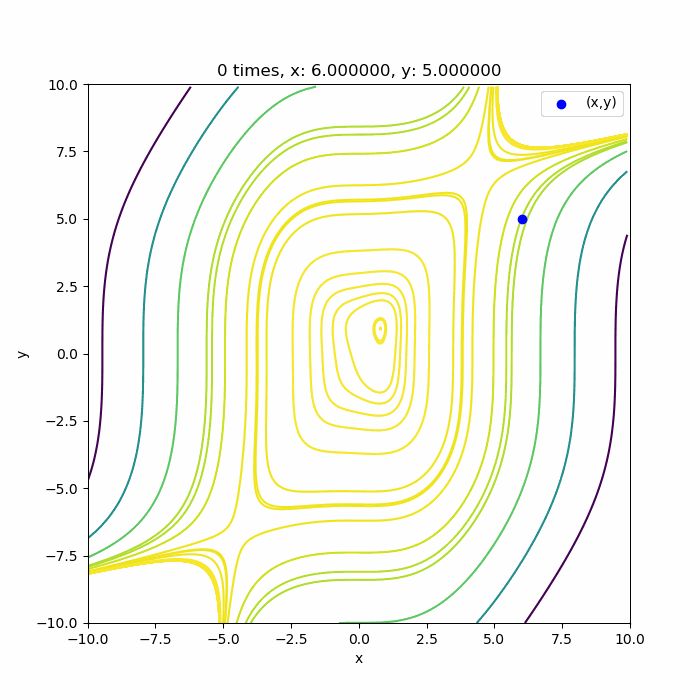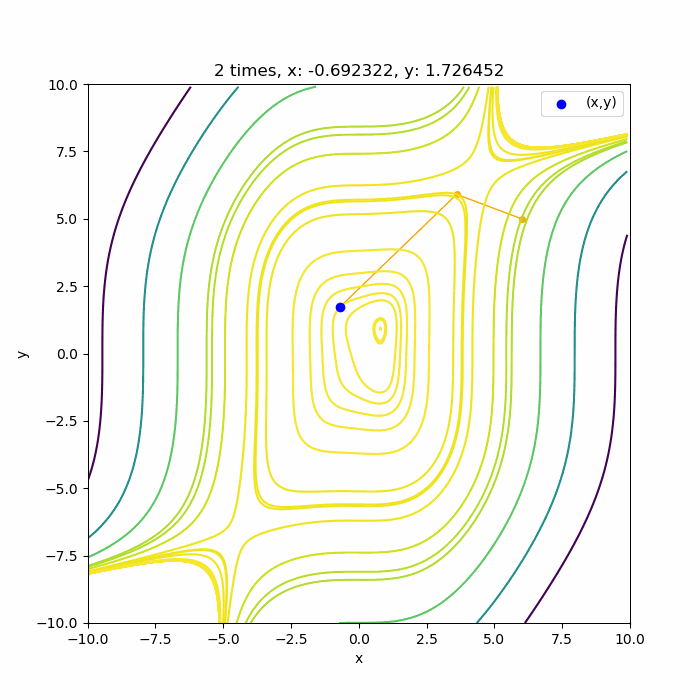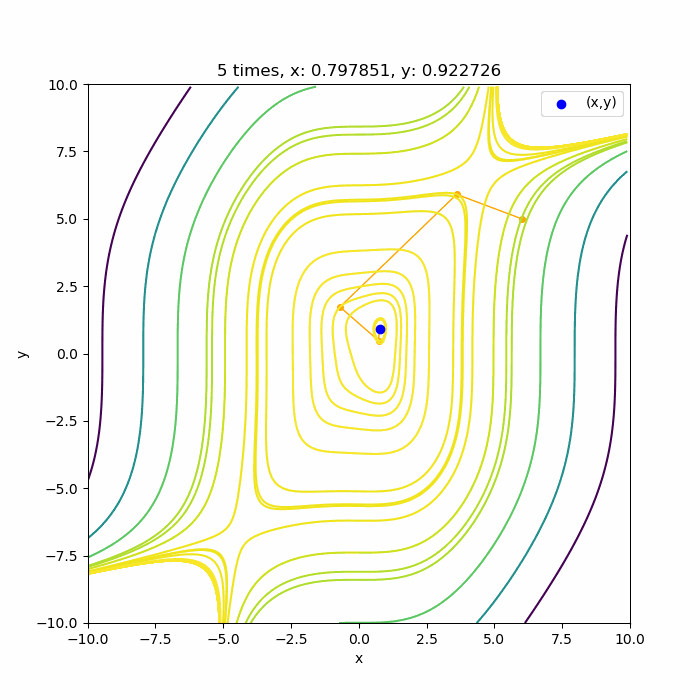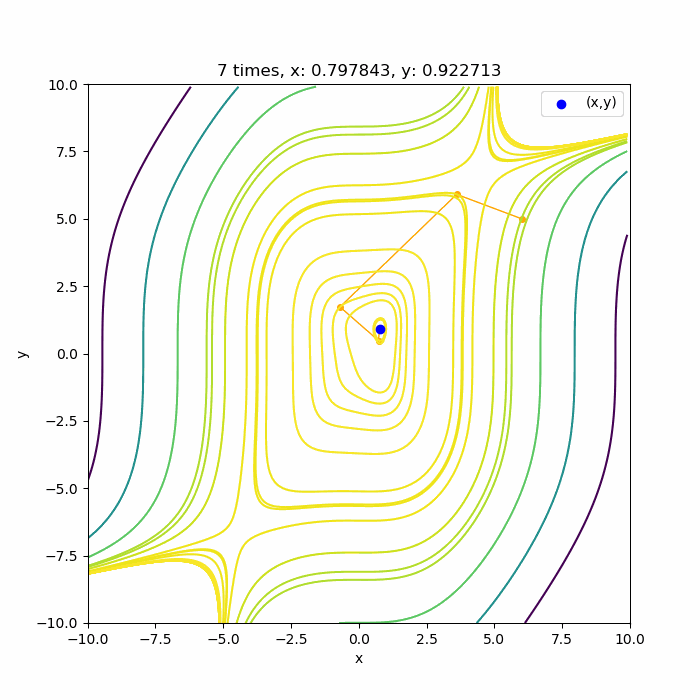
では4次関数 \(f(x,y) = -0.5 x^4 – 0.1 y^4 + 0.01x^3 y^3 + x + 0.3 y \)ではどうなるでしょうか?
いい感じに4回目で極値付近に収束していますね。
共役勾配法をいろいろな関数に適用してみました。なかなか理論通りですね。他の方法と比べてみると面白いかな?
プログラムコード – python
共役勾配な方向に探索を行うクラス – 勾配法
class Search(object):
def __init__(self, func):
# f : function
self.func = func
def diff_func(self, t): #関数の微分を中心差分で求める
delta_h = 0.000001
return (self.func(t + delta_h) - self.func(t - delta_h) ) / ( 2* delta_h)
def search_max(self, initial_t, initial_h, epsiron):
# step 1 : 初期値の設定
t = initial_t
h = initial_h
while abs( self.diff_func(t) ) > epsiron : # step 5 : 収束のチェック
# step 2
h = np.sign( self.diff_func(t) ) * abs(h)
T = t
Td = t + h
if self.func(T) < self.func(Td): # step 3
while self.func(T) <= self.func(Td): # step 3 (a)
h = 2*h
T = Td
Td = T + h
# step 3 (b)
t = T
h = h /2
else: # step 4
while self.func(T) >= self.func(Td): # step 4 (a)
h = h / 2
Td = Td - h
# step 4 (b)
t = Td
h = 2 * h
return t
共役勾配法 – 2変数関数
# 共役勾配法のクラス 2変数クラスを扱う
import numpy as np
class Conjugate_Search(object):
__delta_h = 0.0001
def __init__(self, func):
self.func = func
def dfdx(self, x,y):
return (self.func(x + self.__delta_h, y) - self.func(x - self.__delta_h, y)) / ( 2* self.__delta_h)
def dfdy(self, x,y):
return (self.func(x, y + self.__delta_h) - self.func(x, y - self.__delta_h)) / ( 2* self.__delta_h)
def ddfdxdx(self, x,y):
return (self.dfdx(x + self.__delta_h, y) - self.dfdx(x - self.__delta_h, y)) / ( 2* self.__delta_h)
def ddfdxdy(self, x,y):
return (self.dfdx(x, y + self.__delta_h) - self.dfdx(x, y - self.__delta_h)) / ( 2* self.__delta_h)
def ddfdydx(self ,x,y):
return (self.dfdy(x + self.__delta_h, y) - self.dfdy(x - self.__delta_h, y)) / ( 2* self.__delta_h)
def ddfdydy(self, x,y):
return (self.dfdy(x, y + self.__delta_h) - self.dfdy(x, y - self.__delta_h)) / ( 2* self.__delta_h)
def gradient(self, x): # 勾配の計算
return np.array([self.dfdx(x[0], x[1]), self.dfdy(x[0],x[1])])
def hessian(self, x): # ヘッセ行列の計算
return np.array([[self.ddfdxdx(x[0], x[1]), self.ddfdxdy(x[0], x[1])], [self.ddfdydx(x[0],x[1]), self.ddfdydy(x[0], x[1])]])
def calc_inner(self, a, H, b): # 2次形式の内積計算
r_v = [H[0,0] * b[0] + H[0,1] * b[1], H[1,0]*b[0] + H[1,1]*b[1]]
return (a[0] * r_v[0] + a[1] * r_v[1])
def search(self, initial_x, delta):
x = initial_x
# 初期値の設定
alpha = 0
m = np.array([0,0])
while True:
## 共役勾配な方向を計算
m = self.gradient(x) + alpha * m
## 関数 F(t) の定義
F = lambda t : self.func(x[0] + t * m[0], x[1] + t * m[1])
## 1変数の勾配法
search = Search(F)
## 最大値 t の探索の初期設定
initial_t = 0.01 ## 初期値は常に0.01から始める
initial_h = 0.01
epsiron = 0.001 ## 収束判定
## 勾配法で最大値 tを探索する
max_t = search.search_max(initial_t, initial_h, epsiron)
## 解の方向
x = x + max_t * m
## alphaの更新
numerator = self.calc_inner(m, self.hessian(x), self.gradient(x))
denominator = self.calc_inner(m, self.hessian(x), m)
alpha = - numerator / denominator
## 収束条件の判断
d = np.sqrt((max_t * m[0])**2 + (max_t*m[1])**2)
if d < delta:
break
if np.isnan(x[0]):
break
return x
実行コード
## 共役勾配法で計算する関数定義 func = lambda x, y : -(x**2 - x*y + y**2 - x - y) # 共役勾配法のインスタンス生成 CG = Conjugate_Search(func) # 初期値設定 initial_x = [5,8] # 収束判定の定義 delta = 0.00001 # 共役勾配法の実行 limit_x = CG.search(initial_x, delta) # 結果表示 print(limit_x) # [1.00, 1.00]


コメント