機械学習の内容を理解するため、”これなら分かる最適化数学, 金谷健一”を勉強中です。第3章 関数の最適化のところで、ちょっと理解に苦しんだので、実際に数値計算と、計算途中の数値をビジュアル化してイメージで理解できるようにまとめています。
数値計算のイメージ
一般に多変数関数の極値(最大値、最小値)を解析的に求めることは困難で、数値計算がよく利用されます。数値計算で極値を求める方法はいろいろありますが、その方法はどれも、関数に値を与えながら増加する方向、減少する方向を探していき、その変化量が小さくなるまで(収束するまで)繰り返す方法です。
勾配法はこの極値を求める基本的な方法です。
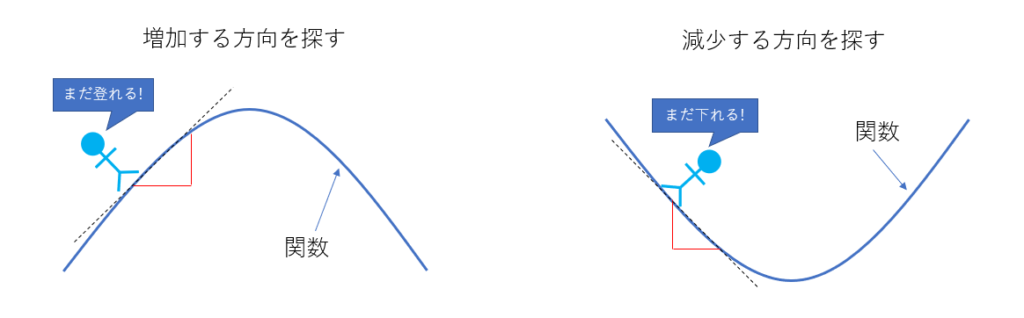
1変数の勾配法のアルゴリズム
詳しくは本に記載されていますが、日本語をアルゴリズム的に描くとこんな感じになります。

Step 3 (a)のイメージ
Step 3 (a)の部分を実際に計算してアニメーションしてみました。関数は最大値がある適当なものを使っています。アニメーションを見ると、hが回数を重ねることに倍になっていき、ついにf(Xd)がf(X)よりも小さくなるところがありますね(4 times)。それから、Xは次の回数でXdとなっているので、回数を重ねる毎に頂点へ近づいていることが分かります。点線はf(X)とf(Xd)を結んだ直線でこの傾きが反転するまで繰り返していますね、つまり今の場所(X)から次の一歩(Xd)が下がったところが登り切った場所だと判断できるのです。ちなみに 0 timesがStep 3のif文の箇所に相当するものです。4 timesでf(Xd)よりもf(X)のほうが大きな値なので、次の探索はXを基準にしたほうがより極値(この場合は極大値)に早く近づくことが分かります。
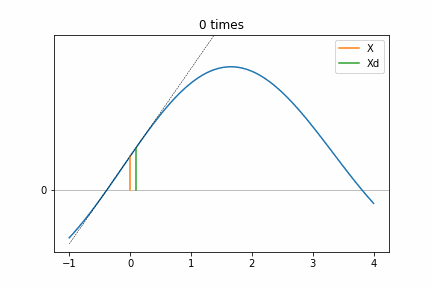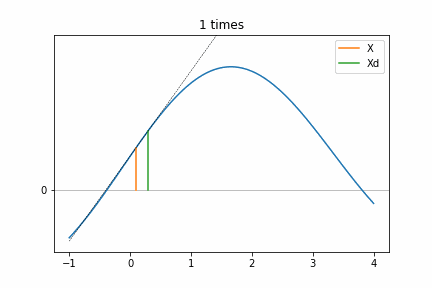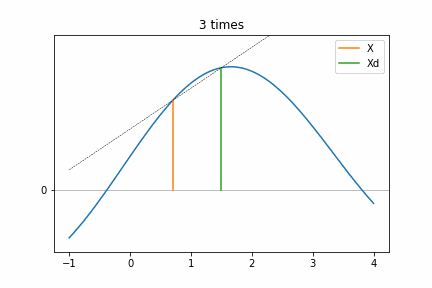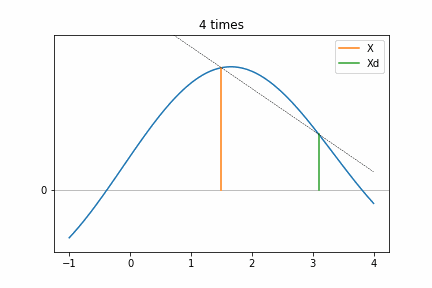
Step 4 (a)のイメージ
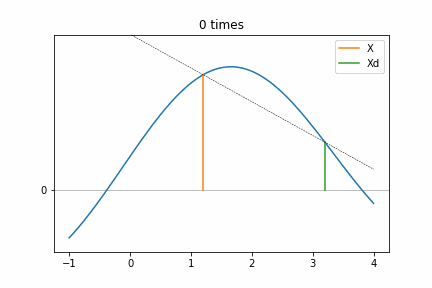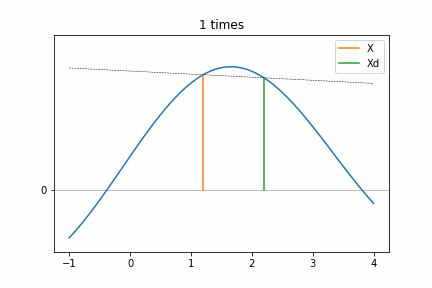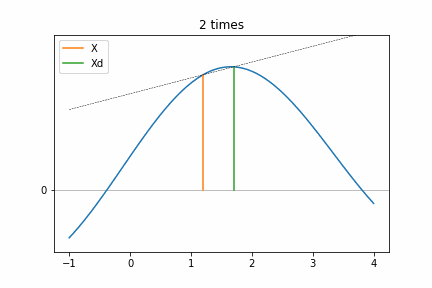
Step 4 (a)をアニメーションさせるとこんな感じになります。Xは固定されたまま、Xdの位置が徐々にXに近づいていっています。この近づき具合は前回のhの半分になっていますね(Xd-Xの幅が回を重ねる毎に半分になっていっています)。山を登るようにXdが変化しているので、そのうち傾きが変化へする場所(2 times)にきて、この探索が完了します。このときf(X)よりもf(Xd)のほうが大きいので、次の探索はXdを基準にしたほうがより極値に近づくことが分かりますね。
極大値を探索するアルゴリズムのイメージ
Step 3とStep 4によりその方向で探索を行い、ついに極値へ収束するアニメーションです。示しているのは勾配法のアルゴリズムのxの値を示しています。Step 3とStep 4 で使用しているXではないのでご注意ください。xの値は”0.0000″から始まって、途中極大値を行き過ぎたりしながら徐々に極大値に近づいています。8 times以降はほとんど変化していませんが、収束判定に使うeによりどれだけ早く収束するか変わります。
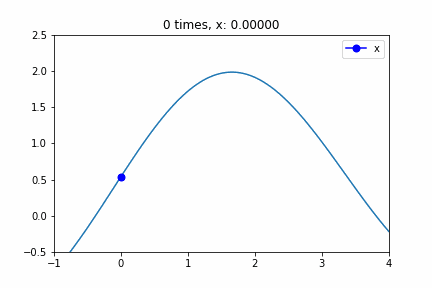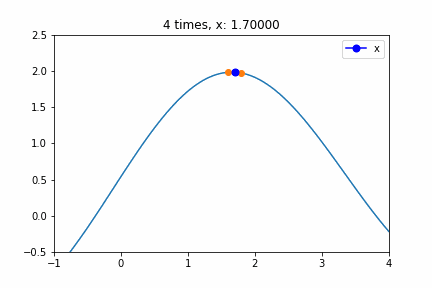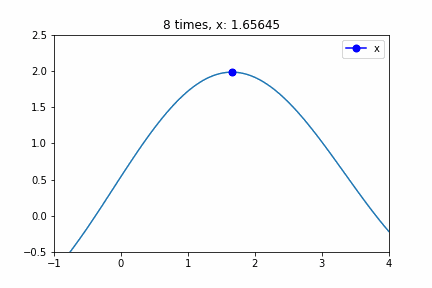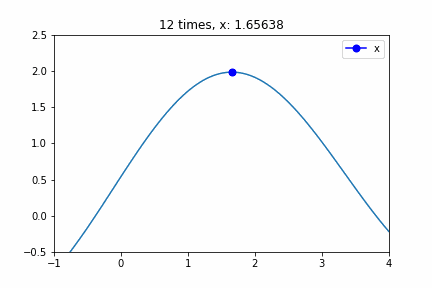
勾配法のアルゴリズムでした。使用したprogramコードはそのうち公開します。
次は多変数の勾配法を記事にします。
コメント