三角関数の直行性の証明などに使用される奇関数と偶関数の性質を確認します。
奇関数の定義
奇関数とは以下の関係となる関数\(g(x)\)のことです。
$$
g(-x) = -g(x)
$$
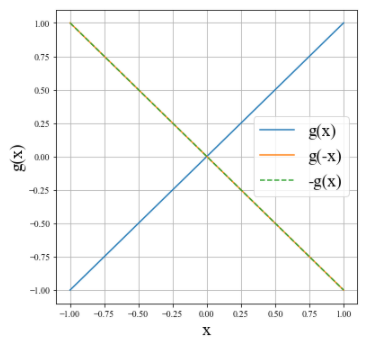
例として、\(g(x) = x^n \) (\(n\)が奇数)があげられます。\(n=1\)として図で示すとこんな感じです。奇関数の性質を示していますね。
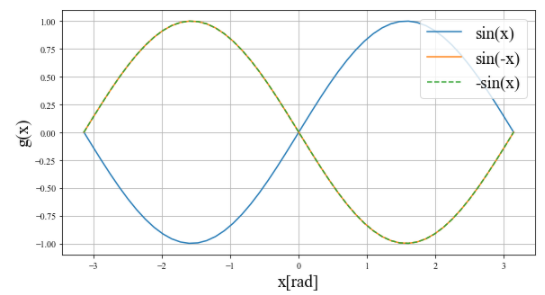
それから、\(Sin\)関数も奇関数です。図で描くとやはり奇関数の性質を示していますね。
偶関数の定義
偶関数とは以下の関係となる関数\(f(x)\)のことです。
$$
f(-x) = f(x)
$$
例として、\(f(x) = x^n \) (\(n\)が偶数)があげられます。\(n=2\)として図で示すとこんな感じです。偶関数の性質を示していますね。

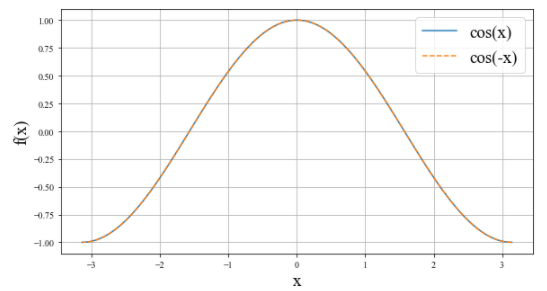
それから、\(cos\)関数も偶関数です。図で示すと偶関数の性質を示していることが分かりますね。
奇関数と偶関数の掛け算
奇関数を \(g_1(x), g_2(x)\)
偶関数を \(f_1(x), f_2(x)\)
とします。
奇関数 x 奇関数 = 偶関数
奇関数と奇関数の掛け算は偶関数になります。
証明
$$
\begin{eqnarray}
A(x) &=& g_1(x) \cdot g_2(x) \\
A(-x) &=& g_1(-x) \cdot g_2(-x) \\
&=& (-g_1(x)) \cdot (-g_2(x)) \\
&=& g_1(x) \cdot g_2(x) \\
&=& A(x)
\end{eqnarray}
$$
偶関数 x 偶関数 = 偶関数
偶関数と偶関数の掛け算は偶関数になります。
証明
$$
\begin{eqnarray}
B(x) &=& f_1(x) \cdot f_2(x) \\
B(-x) &=& f_1(-x) \cdot f_2(-x) \\
&=& f_1(x) \cdot f_2(x) \\
&=& B(x)
\end{eqnarray}
$$
奇関数 x 偶関数 = 奇関数
奇関数と偶関数の掛け算は奇関数になります。
証明
$$
\begin{eqnarray}
C(x) &=& g_1(x) \cdot f_1(x) \\
C(-x) &=& g_1(-x) \cdot f_1(-x) \\
&=& -g(x) \cdot f_1(x)\\
&=& -C(x)
\end{eqnarray}
$$
奇関数と偶関数の定積分
ある関数\(h(x)\)を区間[-T,T]で定積分することを考えます。
$$
\int_{-T}^{T} h(x) dx
$$
先に答えを言うと、
\(h(x)\)が奇関数なら、
$$
\int_{-T}^{T} h(x) dx = 0
$$
\(h(x)\)が偶関数なら、
$$
\int_{-T}^{T} h(x) dx = 2 \int_{0}^{T} h(x) dx
$$
になります。
証明
まず積分を次のように分解します。
$$
\int_{-T}^{T} h(x) dx = \int_{-T}^{0} h(x) dx + \int_{0}^{T} h(x) dx
$$
この分解した右式の第一項を\(y=-x\)で変数変換を行います。
すると、
$$
\begin{eqnarray}
&&\frac{dy}{dx} = -1 より dx = -dy \\
&&x = -T のとき y = T \\
&&x = 0 のとき y = 0
\end{eqnarray}
$$
以上より、
$$
\begin{eqnarray}
\int_{-T}^{T} h(x) dx &=& \int_{-T}^{0} h(x) dx + \int_{0}^{T} h(x) dx \\
&=& \int_{-T}^{0} h(-y) (- dy) + \int_{0}^{T} h(x) dx \\
&=& -\int_{-T}^{0} h(-y) dy + \int_{0}^{T} h(x) dx \\
&=& \int_{0}^{T} h(-y) dy + \int_{0}^{T} h(x) dx \\
\end{eqnarray}
$$
ここまで展開できます。
\(h(x)\)が奇関数の場合
奇関数の場合、\(h(-x) = -h(x)\)なので、第二項と打ち消しあい定積分の結果はゼロになります。
$$
\begin{eqnarray}
\int_{-T}^{T} h(x) dx &=& \int_{0}^{T} h(-y) dy + \int_{0}^{T} h(x) dx \\
&=& -\int_{0}^{T} h(y) dy + \int_{0}^{T} h(x) dx \\
&=& 0
\end{eqnarray}
$$
\(h(x)\)が偶関数の場合
偶関数の場合、\(h(-x) = f(x)\)なので、第一項と第二項が共通となります。
$$
\begin{eqnarray}
\int_{-T}^{T} h(x) dx &=& \int_{0}^{T} h(-y) dy + \int_{0}^{T} h(x) dx \\
&=& \int_{0}^{T} h(y) dy + \int_{0}^{T} h(x) dx \\
&=& 2\int_{0}^{T} h(x) dx
\end{eqnarray}
$$


コメント