平方根をニュートン法で求めてみます。この記事でのニュートン法は最大値、最小値を求めるニュートン法ではなく、 \(y=ax + b\)のような方程式の解を求めるニュートン法です。 ちょっと混乱するかもしれませんが、しっかり理論的なところも説明します。動作のアニメーションもあるのでイメージもできると思います。
平方根を変形して図を描く
平方根は\(x = \sqrt{2}\)を計算すると\(x = 1.41421356237 \)と求められますよね。Excelなどのソフトで計算できますけど、これを数値計算:ニュートン法で求めていきます。
まず、両辺を2乗して\(x^2 = 2\)とします。そして(1)式のように”\( = 0\)”とする方程式を定義します。
$$
f(x) = x^2 -2 = 0 \tag{1}
$$
この方程式の\(x = [0 , 4.0]\)の範囲で描くと、こんな感じの青線のグラフになります。ここから、青線と\(f(x)=0\)のラインが交わるところが 解\(x = 1.41421356237 \)になるということが分かります。
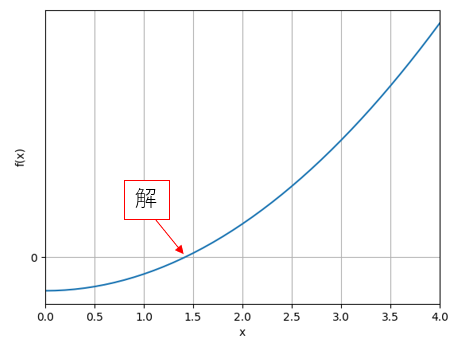
ということで、この交点を求めることが平方根の解を求めることになりますね。
ゼロとの交点を求める
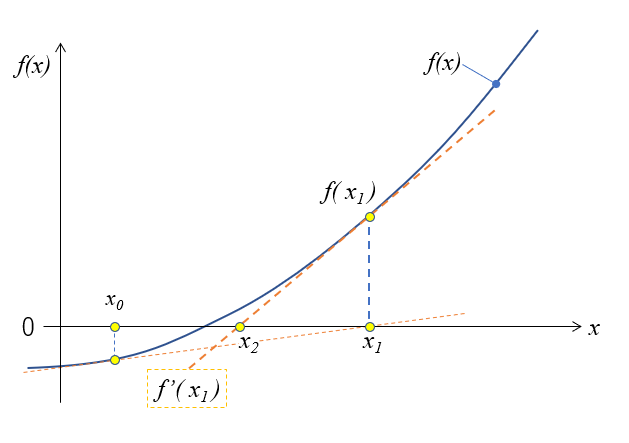
例えば適当な\(x = x_0\)を設定し、そこでの\(f(x)\)の傾き\(f^{\prime}(x_0)\)を図に描きます。
こんな感じになりますね。 \(f^{\prime}(x_0)\) と\(f(x)=0\)の交点\(x_1\)は、\(x_0\)よりも解に近づいていますね。
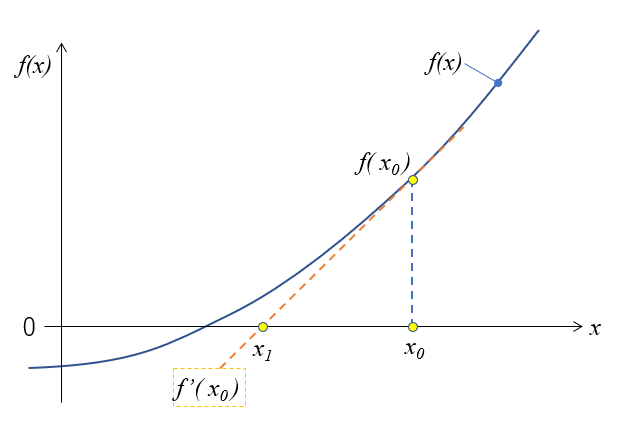
\(x_1\)は、 図の三角形の関係:\(f^\prime(x_0) = f(x_0) / (x_0 – x_1)\)より(2)式になります。
$$
x_1 = x_0 – f(x_0) / f^\prime(x_0) \tag{2}
$$
具体的に数値で書くと、\(f^\prime(x) = 2 x\)より(3)式になります。
$$
\begin{eqnarray}
x_1 &=& x_0 – (x_0 ^2 – 2) / (2 x_0) \\
&=& \frac{1}{2} \bigl( x_0 + \frac{2}{x_0} \bigr) \tag{3}
\end{eqnarray}
$$
次は求めた\(x_1\)を使い、 傾き\(f^{\prime}(x_1)\)とそのゼロとの交点\(x_2\)を描くとこうなります。
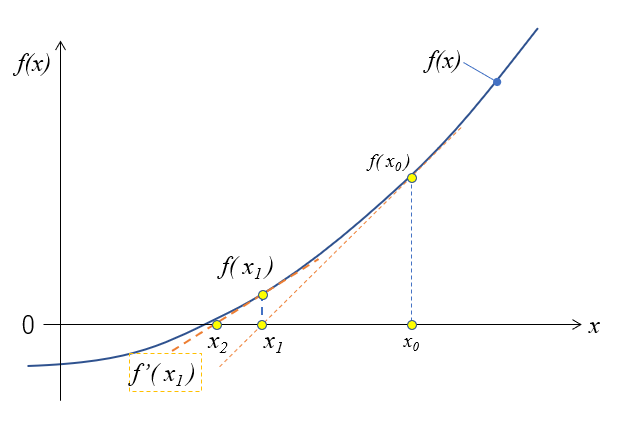
だんだん解に近づいていますね。
ここでの\(x_2\)は(2)式、(3)式と同じようになるので、代数的に書くと(4)式、具体的に書くと(5)式です。
$$
\begin{eqnarray}
x_2 &=& x_1 – f(x_1) / f^\prime(x_1) \tag{4} \\
&=& \frac{1}{2} \bigl( x_1 + \frac{2}{x_1} \bigr) \tag{5}
\end{eqnarray}
$$
この更新を続けていけば徐々に解に近づいていきます。
\(x_{n+1}\)が解を通り過ぎて左側へは行きません。なぜかというと、\(f(x) = 0\)となる、\(x_n\)では、次の点は\(x_{n+1} = x_n – f(x_n) / f^\prime(x_n)\)と計算できますが、\(f(x_n) = 0\)ということから、\(x_{n+1} = x_n\)となるからです。
また、傾きを使った関係からこの方法では\(f(x) = 0 \)となる解\(x_n\)は求めることが出来ません。テイラー展開で考えたように、近似式の関係から次の点を求めているので、解から少しずれるからです。これは三角形が無限に続くと考えられます。
そこで、この更新式は\(\sigma > (x_{k+1} – x_k) \)まで繰り返すという条件にします。
このように、三角形の関係式を更新して方程式の解を求める方法:(6)式をニュートン法といいいます。
$$
x_{k+1} = x_k – f(x_k) / f^\prime(x_k) \tag{6}
$$
具体的に計算していくと、このような収束計算になります。\(x_0 = 3.0\)から始めってだんだん解に近づいて行っていますね。
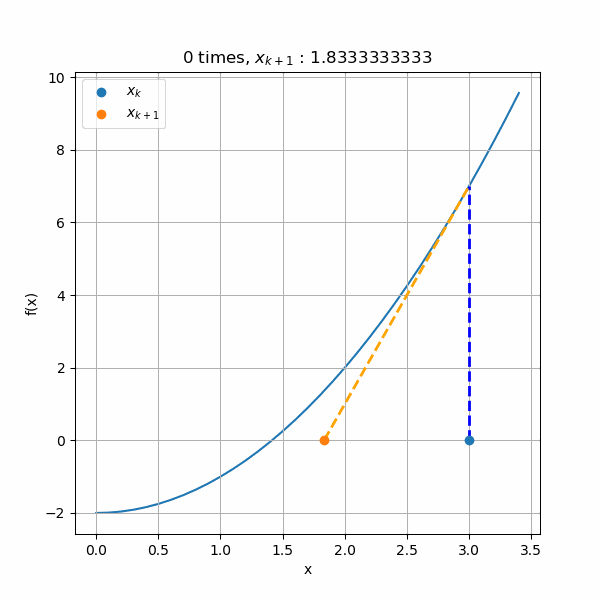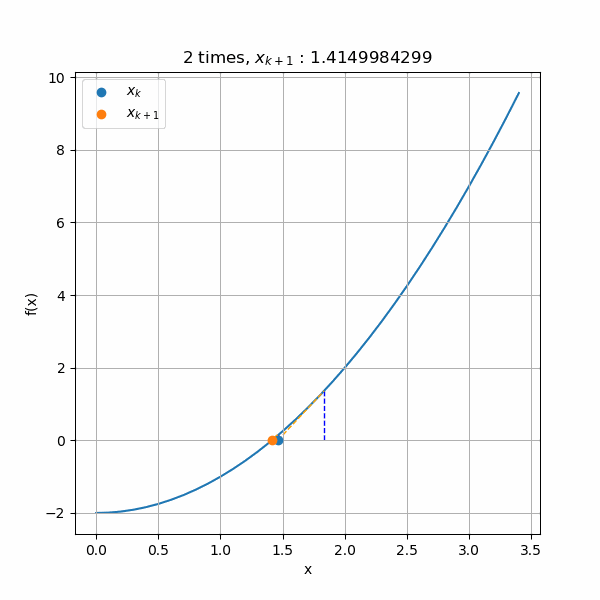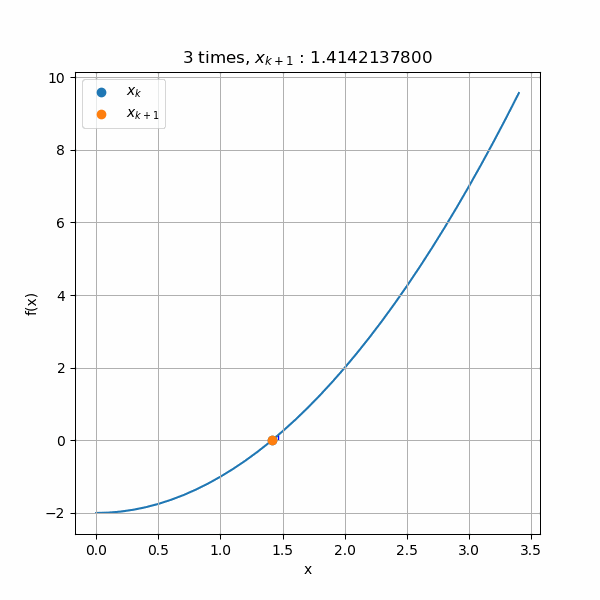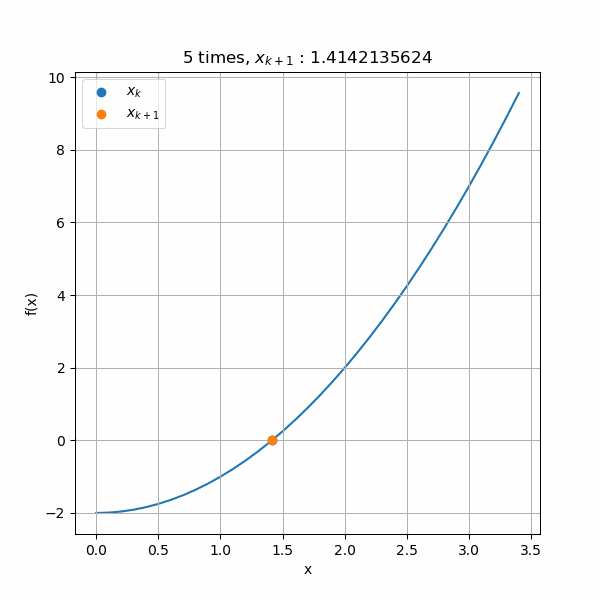
上の図では4回目以降の収束が分からないので、収束毎に三角形をズームしたアニメーションを作成しました。縦軸と横軸のスケール変化に注目してもらうと、ものすごく小さな数値のところまで計算されていますね。でも三角形はずっと保たれています。また、最後の5回目の計算では青線の\(f(x)\)のがガタガタしていますが、これは表示の問題です。
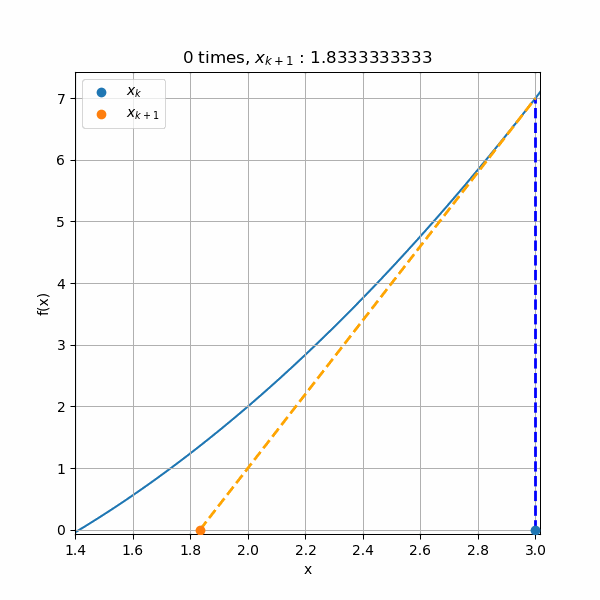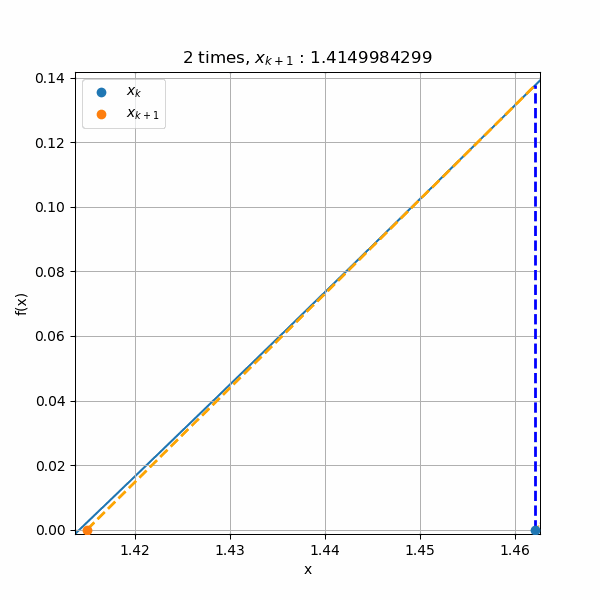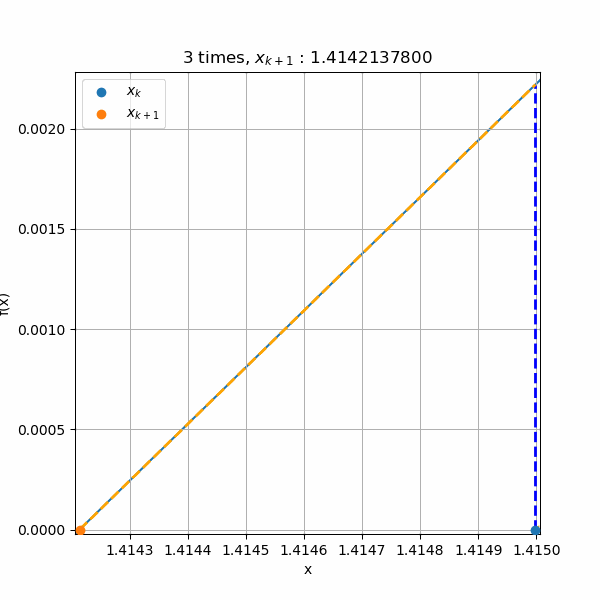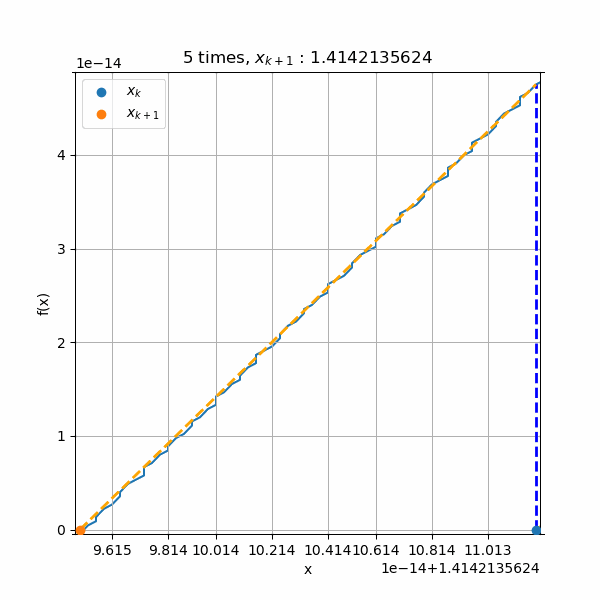
マイナス側からの収束
これまでは最初の計算を解のプラス側から行い収束させましたが、解のマイナス側からスタートしていみます。
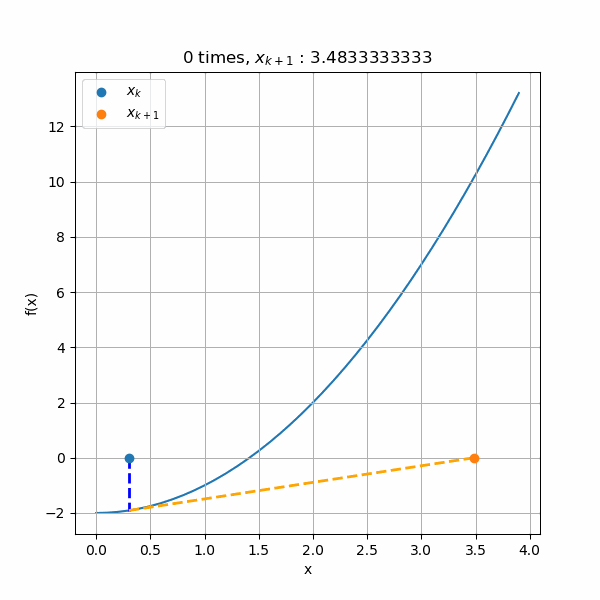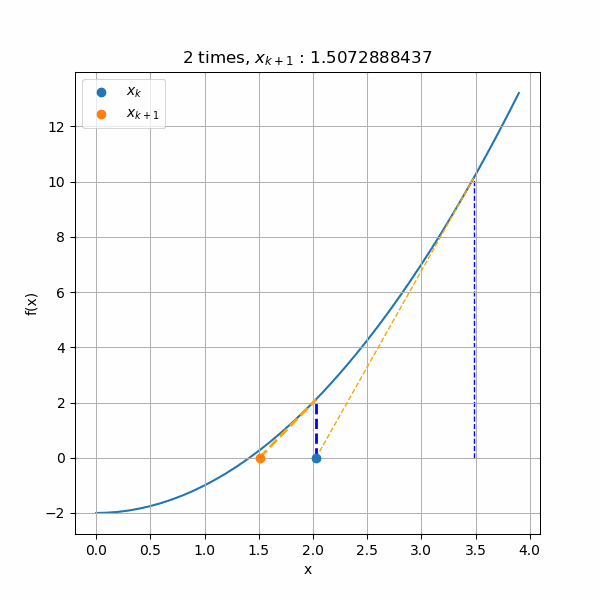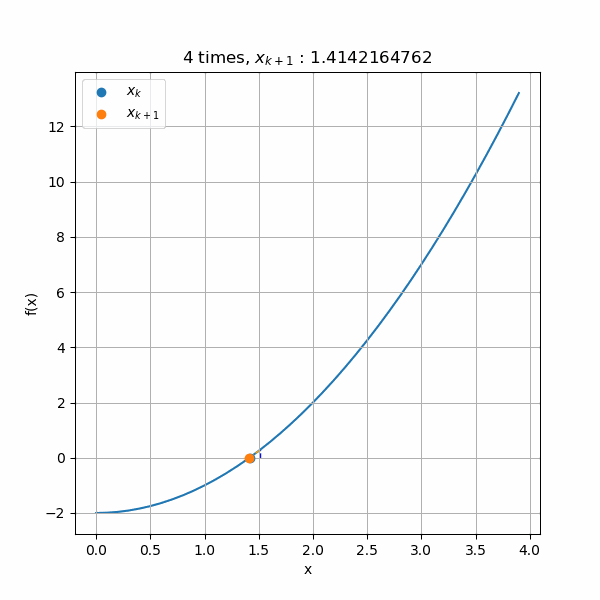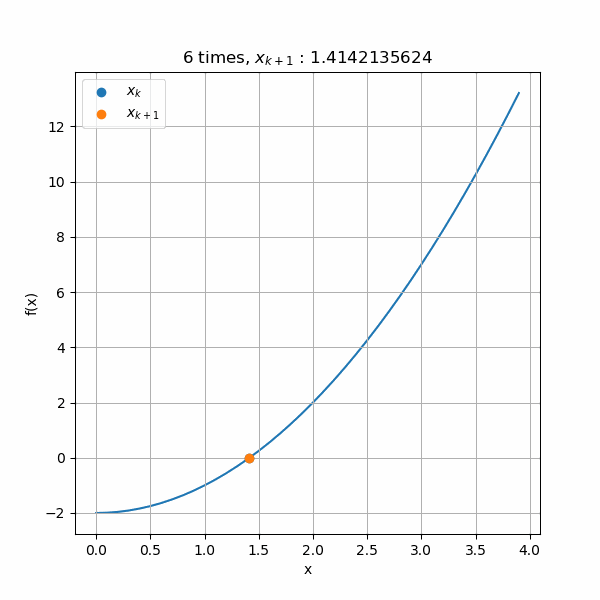
\(x_0\)を解の左において\(x_1\)を求めると、こんな感じになり、\(x_1\)が解の右側に計算されます。
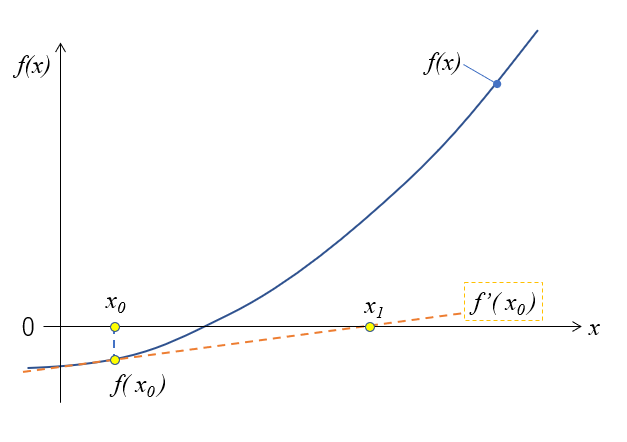
この\(x_1\)を使い\(x_2\)を計算すると、プラス側から収束していく計算が始まるので、やはり同じ収束計算で解が求めることになります。うまくできていますね。
実際に具体に計算していみると、このようなアニメーションになります。最初は解の左側からスタートしていますが、2回目からは右から収束していますね。
ニュートン法で平方根を計算できたので、次は一般的な根の計算をニュートン法で行います。
プログラムコード – Python
1. アルゴリズムそのまま
\(f(x) = x^2 – 2\)、 \(x_{k+1} = x_k – f(x_k) / f^\prime(x_k)\)の更新式をプログラムしてみます。
ニュートン法のクラス
class Newton(object):
def __init__(self, func, d_func):
self.func = func
self.d_func = d_func
def root(self, initial_x, sigma):
x0 = initial_x
while True:
x = x0 - self.func(x0) / self.d_func(x0)
if abs(x - x0) < sigma:
break
else:
x0 = x
return x
実行
import numpy as np # 平方根の方程式とその微分の定義 f = lambda x : x**2 - 2 df = lambda x:2*x # 初期値と収束条件の定義 initial_x = 3.0 sigma = 0.00001 # ニュートン法により平方根の解を計算 newton = Newton(f, df) y = newton.root(initial_x, sigma) print(y) # 出力 : 1.4142135623746899
2. 平方根の計算コード
上の実装では、関数に求めたい平方根の値が定義されていたので、これを入力の平方根を求めるように変更します。
平方根をニュートン法で求める関数
def sqrt_newton(value, sigma):
f = lambda x : x**2 - value
df = lambda x:2*x
x0 = 3 # 初期値
while True:
x = x0 - f(x0) / df(x0)
if abs(x - x0) < sigma:
break
else:
x0 = x
return x
実行
# 値の設定 value = 2 sigma = 0.0000001 # ニュートン法により平方根の計算 root = sqrt_newton(value, sigma) print(root) # 出力 : 1.414213562373095
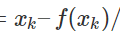
コメント