1階常微分方程式の解曲線を数値計算で求めてみます。解曲線とは微分方式の解\(y(x) = \phi(x)\)が表す曲線のことをいい、この曲線を勾配によって描くことで、微分方程式の解を数値計算で求めることが出来ます。
$$
\frac{d y(x)}{dx} = f(x,y)
$$
ご注意。結構長いです。
解曲線と勾配場
関数 \(y(x) = \phi(x)\)が\(F(x, \phi(x), \phi^\prime(x), \cdots, \phi^{(n)}(x)) = 0\)を満たすとき、 \(y(x) = \phi(x)\) はこの微分方程式の解になります。
そして、 \(y(x) = \phi(x)\) が表す曲線を、その微分方程式の解曲線といいます。
例えば微分方程式 \(x y^\prime – 2 y = 0\)の解は \(y(x) = c x^2\)になります。
計算すると、
$$
y^\prime(x) = 2 c x \Rightarrow 2 c x^2 – 2 c x^2 = 0
$$
ということで、 \(y(x) = c x^2\) は微分方程式 \(x y^\prime – 2 y = 0\) の解です。ちなみに、このように変数が一つだけ(\(x\))の微分方程式を常微分方程式といいます、そして微分方程式中の微分が1階だけのものを1階微分方程式といい、あわせて1階常微分方程式といいます。
では 解\(y(x) = c x^2\)を\(c=1\)として解曲線を描きます。
ただの曲線の図ですね。
今数式の形をした解\(y(x) = c x^2\)から図の解曲線を描きましたが、この逆、図の解曲線から数式の形をした解を求めることを考えます。
まず、1階常微分方程式\(\frac{d y(x)}{dx} = f(x,y)\)の解が\(y(x) = \phi(x)\)であるなら、 \(y(x) = \phi(x)\) 上の任意の点\(x\)における傾きは \(f(x,y)\)であるということを意味しています。
つまり、\(f(x,y)\)を傾きと捉えて、縦軸を\(y\)に、横軸を\(x\)に取ったグラフの各ポイント\(x,y\)で傾き\(f(x,y)\)を描きます。 この傾きを接線とする曲線を\(y(x) = \phi(x)\)で描くことが出来れば、それが解曲線となり、 \(y(x) = \phi(x)\) が \(\frac{d y(x)}{dx} = f(x,y)\) の解であると言えます。
では具体的に各ポイントの傾きを描いてみます。
まず、微分方程式は\(x y^\prime – 2y = 0\)なので、 これを\(\frac{d y(x)}{dx} = f(x,y)\)の形へ書き換えます。すると(1)式のようになり、この式の右辺が傾きを表します。
$$
y^\prime = 2 y / x \tag{1}
$$
例えば\((x,y) = (1,1)\)における傾きは、\(y^\prime = 2y/x = 2 \cdot 1/1 = 2\)で描けます。
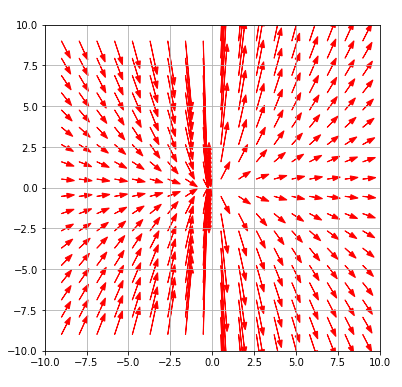
傾きとその大きさを矢印で描いています。このような図を勾配場といいます。
左側から入って原点(0,0)を通り、右側の上下へ向かうような曲線が描けそうですね。この \(y^\prime = 2 y / x\)の解は\(y(x) = c x^2 \)なので、\(c = 2\)と\(c=-2\)とした解曲線をこのグラフに描くとこうなります。下に凸になっている曲線が\(c=2\)の解曲線、上に凸になっている曲線が\(c=-2\)の解曲線です。
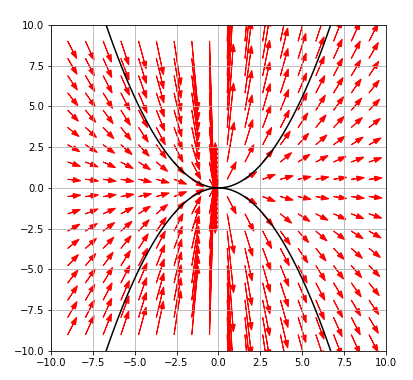
このように、傾きに沿うように曲線を描けば、それが解曲線として採用できそうですね。
オイラー法
では傾きに沿った曲線を描いていきます。出発点\(x_0,y_0\)を決め、そこでの傾き\(f(x_0,y_0)\)を計算します。そして次の点\((x_1, y_1)\)を\(x_1 = x_0 + h\)、\(y_1 = y_0 + h \cdot f(x_0, y_0)\)とします。また次の点\((x_2,y_2\)を傾きかた求めていきます。
このような方法をオイラー法といいます。それから、出発点 \(x_0,y_0\) を決めることを初期値問題といいます。なぜ初期値問題というかというと、微分方程式を解くとは、すべての解を求めることを言うからです。つまり、すべての解曲線を描くことを言います。
オイラー法の図的な意味
オイラー法を図で描くことこんな感じです。
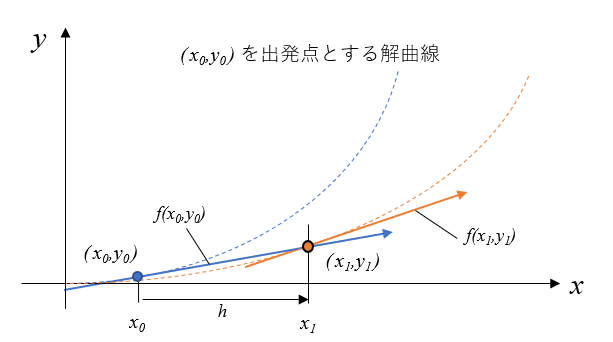
説明のため点線で解析解を描いています。\((x_0, y_0)\)での傾き\(f(x_0, y_0)\)を使い次の点\((x_1, y_1)\)を求めると、\((x_0, y_0)\)を出発点とする解曲線(青破線)からずれます。そして次の点\((x_1, y_1)\)ではその点を通る別の解曲線の傾き\(f(x_1,y_1)\)が計算されます。これを続けると最終的に結構ずれていきます。
オイラー法で数値計算
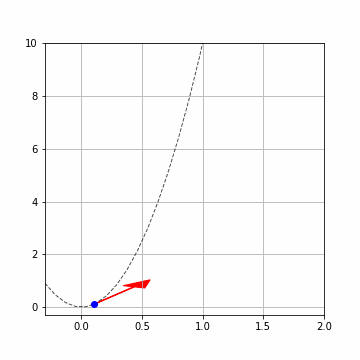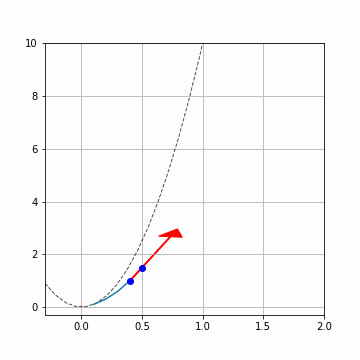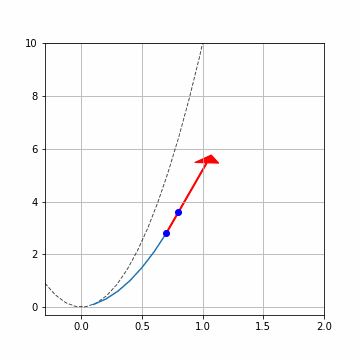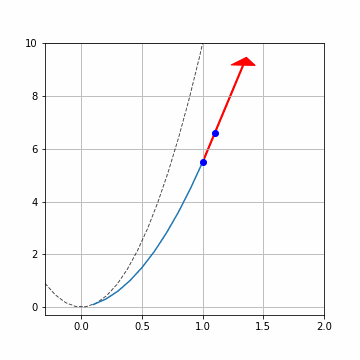
黒の破線が解析解です。矢印が\(x_i, y_i\)における傾き\(f(x_i, y_i)\)です。青点で\((x_i,y_i),(x_{i+1}, y_{i+1})\)を描いています。計算を進める毎に結構ずれていきますね。
ここでは\(h=0.1\)と結構多めにとっているので、ずれが大きくなっています。
オイラー法のプログラム – Python –
# 傾き関数
def dy(x,y):
dy = (2*y/x)
dx = 1
return [ dx, dy]
# 初期値
x0 = 0.1
y0 = 0.1
# 数値列
x_array_euler = [x0]
y_array_euler = [y0]
# オイラー法による計算
xp = x0
yp = y0
dl = 0.1
for i in range(100):
dy_p = dy(xp, yp)
x_next = xp + dy_p[0] * dl
y_next = yp + dy_p[1] * dl
x_array_euler.append(x_next)
y_array_euler.append(y_next)
xp = x_next
yp = y_next
ホイン法
オイラー法は今のポイントだけを使って次のポイントを計算していたのでずれが大きく出ました。そこで、少し進んだ先のポイントの情報を使って次のポイントを計算することを考えます。この方法の一つにホイン法があります。
例えば\((x_0, y_0)\)のポイントから少し先に進んだポイントの傾きは、その解曲線が向かう方向を示していますね。そこで、次のようにして先のポイントの情報を使って解曲線を描きます。
ホイン法のアルゴリズム
Step 1: \((x_i, y_i)\)での傾き\(f(x_i, y_i)\)から、\(k_1\)を(2)式で計算します。この\(k_1\)は\(y\)軸上の値です。
$$
k_1 = h \cdot f(x_i, y_i) \tag{2}
$$
Step 2: 計算した\(k_1\)を使い、\((x_{i} + h , y_{i} + k_1)\)での傾き\(f( x_{i} + h , y_{i} + k_1)\)から\(k_2\)を(3)式で計算します。
$$
k_2 = h \cdot f( x_{i} + h , y_{i} + k_1) \tag{3}
$$
Step 3: \(k_1, k_2\)を使い、次の点 \(y_{i+1}\)を(4)式で計算します。
$$
y_{i+1} = y_i + (k_1 + k_2) / 2 \tag{4}
$$
この方法をホイン法といいます。ホイン法はテイラー展開の2階微分までを考慮したものと捉えることが出来ます。
ホイン法の図的な意味
Step 1とStep 2を図で説明すると以下のようになります。
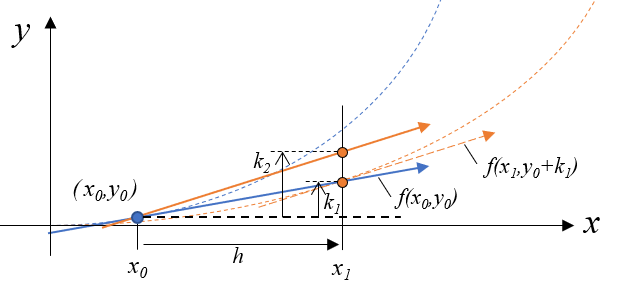
初期値は\((x_0, y_0)\)です。ここでの傾き\(f(x_0,y_0)\)から\(x_1 := x_0 + h\)における\(y\)軸上の値\(k_1\)を算出します。この\(k_1\)は傾き \(f(x_0,y_0)\) が\(h\)だけ進んだ時の高さに相当しているので、図の黒水平破線からの高さです。
そして点\((x_1, y_0 + k_1)\)における傾き\(f( x_1, y_0 + k_1)\) から\(k_2\)を算出します。\(k_2\)も傾き \(f( x_1, y_0 + k_1)\) が\(h\)だけ進んだ時の高さに相当するものです。なので、オレンジ破線で描いた傾き \(f( x_1, y_0 + k_1)\) を\((x_0,y_0)\)の位置から伸ばし、\(h\)分進んだ場所が\(k_2\)になります。
次の\(y_{i+1}\)の計算で用いる\((k_1 + k_2)/2\)の位置は図のように、\(k_1\)と\(k_2\)の中間です。この点もまだ黒水平破線からの高さです。
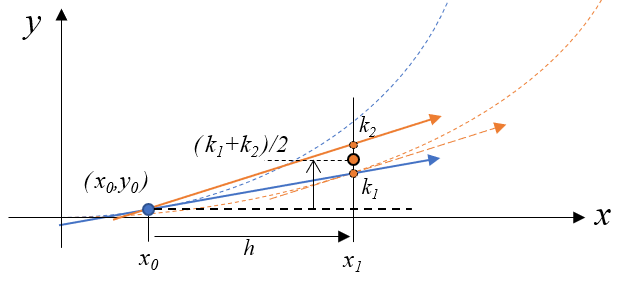
この\((k_1 + k_2) / 2\)の点は、図では既に\(y_0\)分高くなっているものです。\(y_1 = y_0+ (k_1 + k_2) / 2\)なので、この点が\((x_1, y_1)\)として求まります。
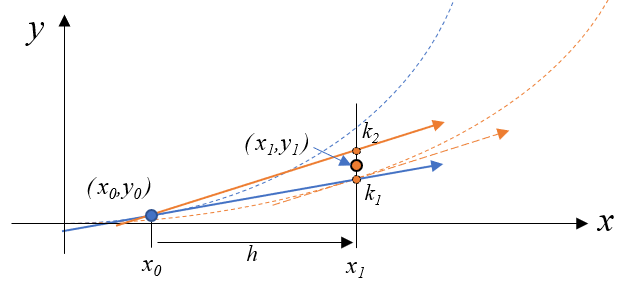
ホイン法は次の進むべき方向を考慮することでオイラー法よりも解析解に近くなりました。でも図から分かるようにまだやっぱりずれが生じています。
ホイン法で数値計算
プログラムで計算すると以下のように進むごとにずれていますね。
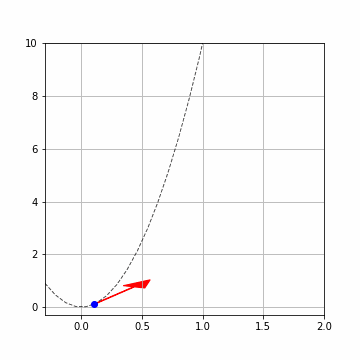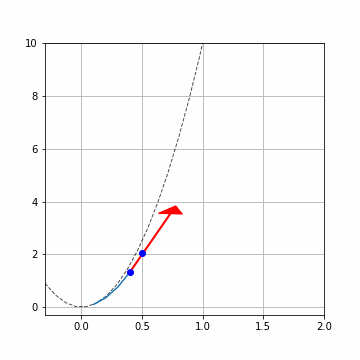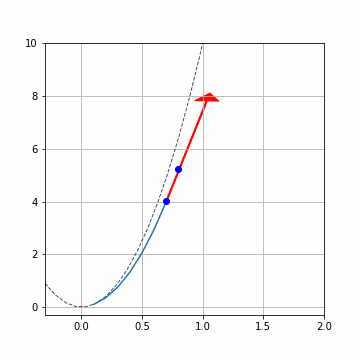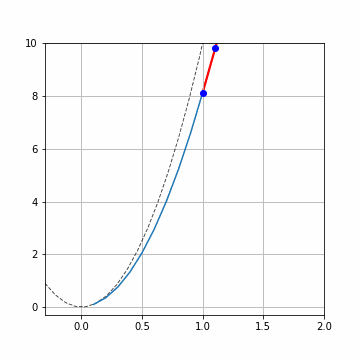
赤い矢印は傾き\(f(x_i,y_i)\)です。青い点で\((x_i,y_i),(x_{i+1},y_{i+1})\)を示しています。
ホイン法はテイラー展開の2階微分の項までを考慮した方法です。今回の微分方程式の解は\(y(x) = c x^2\)なので、ホイン法でもずれが生じるのは不思議です。
ホイン法のプログラム – Python –
# 傾き関数
def dy(x,y):
dy = (2*y/x)
dx = 1
return [dx, dy]
# 初期値
x0 = 0.1
y0 = 0.1
# 数値列配列
x_array_hoin = [x0]
y_array_hoin = [y0]
# ホイン法で計算
xp = x0
yp = y0
dl = 0.1
for i in range(100):
dy_p = dy(xp, yp)
x_pn = xp + dl
k1 = dy_p[1] * dl
dy_n = dy(x_pn, yp + k1)
k2 = dy_n[1] * dl
x_next = x_pn
y_next = yp + (k1 + k2)/2
x_array_hoin.append(x_next)
y_array_hoin.append(y_next)
xp = x_next
yp = y_next
勾配場の少し先の情報を一つだけ使っても解析解に近い値が出せないことが分かりました。先の情報をもっと沢山使えばもっと解析解に近い値が出せそうですね。この方法の一つにルンゲクッタ法というものがあります。
ルンゲクッタ法
ルンゲクッタ法はテイラー展開の4階微分の項までを考慮する方法です。そのアルゴリズムは次のようなものです。
ルンゲクッタ法のアルゴリズム
点\((x_i, y_i)\)の次の点 \((x_{i+1}, y_{i+1})\) を
$$
\begin{eqnarray}
k_1 &=& h \cdot f(x_{i}, y_{i}) \\
k_2 &=& h \cdot f(x_{i} + h/2 , y_{i} + k_1/2) \\
k_3 &=& h \cdot f(x_{i} + h/2 , y_{i} + k_2/2) \\
k_4 &=& h \cdot f(x_{i} + h , y_{i} + k_3) \\
\end{eqnarray}
$$
のように\(k_1,k_2,k_3,k_4\)を計算してから、(5)式のように計算する方法です。
$$
\begin{eqnarray}
y_{i+1} &=& y_{i} + (k_1+ 2k_2 + 2k_3 + k_4) /6\\
x_{i+1} &=& x_i + h
\end{eqnarray} \tag{5}
$$
この計算方法がテイラー展開の4階微分までを考慮しているかを確かめるにはかなりの計算力が必要です。興味のある方は京都大学の早川先生が公開しているノートを見てみてください。
とはいえ、理解できないのも何なので、絵に描いてどんなことをしているのか確認してみます。
ルンゲクッタ法の図的な意味
\(k_1\)の計算
\((x_0,y_0)\)から \((x_1,y_1)\)を計算することを考えます。
まず \(k_1\)は(6)式で計算されるので、図では\(x_1\)における点として描けます。\(k_1\)は傾き\(f(x_0,y_0)\)が\(h\)進んだ場所の高さなので、図では黒水平破線からの高さです。
$$
k_1 = h \cdot f(x_{0}, y_{0}) \tag{6}
$$
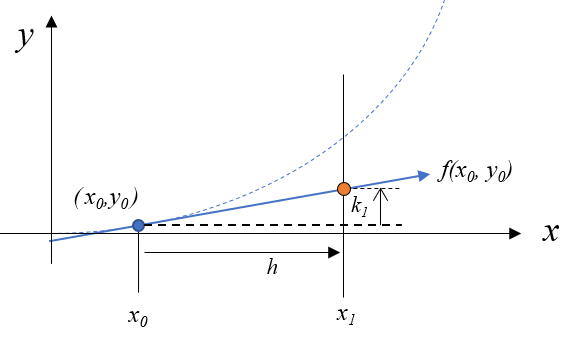
\(k_2\)の計算
\(k_2\)は先ほど計算した\(k_1\)を使い、(7)式で計算されます。図では\(k_1\)より少し上の場所に描かれます。この\(k_2\)は\((x_h/2, y_0 + k_1/2)\)での傾き\(f(x_h/2, y_0 + k_1/2)\)が\(h\)進んだ場所の高さなので、図では黒水平破線からの高さです。
$$
k_2 = h \cdot f(x_{0} + h/2 , y_{0} + k_1/2) \tag{7}
$$
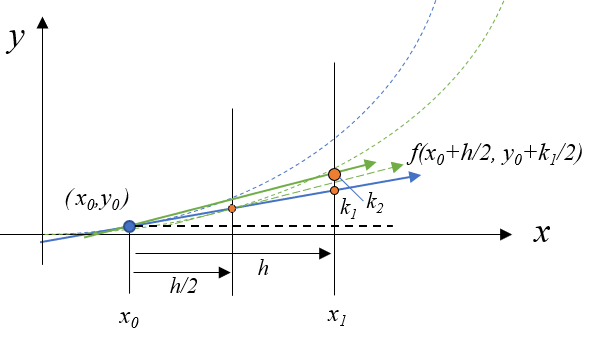
\(k_3\)の計算
\(k_3\)は計算した\(k_2\)を使い、(8)式で計算されます。\((x_0+h/2, y_0+k_2/2)\)における傾き\( f(x_0+h/2, y_0+k_2/2)\) が\(h\)進んだ高さが\(k_3\)です。図では黒水平破線からの高さです。
$$
k_3 = h \cdot f(x_{0} + h/2 , y_{0} + k_2/2) \tag{8}
$$
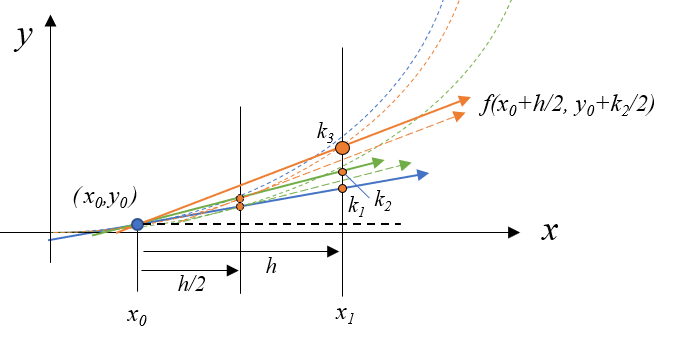
\(k_4\)の計算
\(k_4\)は計算した\(k_3\)を使い(9)式で計算されます。\((x_0+h, y_0+k_3)\)における傾き\(f(x_0+h, y_0+k_3)\)が\(h\)進んだ高さが\(k_4\)です。図では黒水平線からの高さです。
$$
k_4 = h \cdot f(x_{0} + h , y_{0} + k_3) \tag{9}
$$
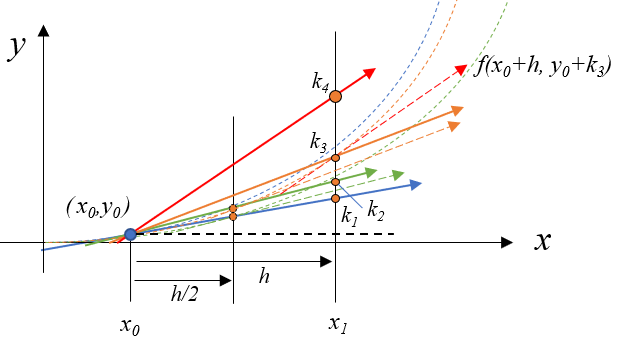
\((k_1 + 2 k_2 + 2 k_3 + k_4)/6\)と\(y_{i+1}\)の計算
\(y_0\)の次の点\(y_1\)は計算した\(k_1,k_2,k_3,k_4\)を用いて(10)式で計算されます。そこでまず、\(y_0\)に加算される\((k_1 + 2 k_2 + 2 k_3 + k_4)/6\)の位置を求めます。
$$
y_{1} = y_{0} + (k_1+ 2k_2 + 2k_3 + k_4) /6 \tag{10}
$$
図に描いて6分の一の高さとした場所を描くと、今回は下図のような\(k_3\)に近い点になりました。分割の方法は製図の本などを参考にしてみてください。この\((k_1+2k_2+2k_3+k_4)/6\)の高さは黒水平破線からの高さ \(k_1,k_2,k_3,k_4\)を演算したものなので、やはり黒水平破線からの高さです。
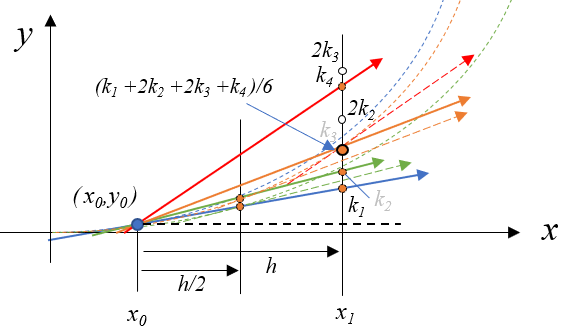
この\((k_1+2k_2+2k_3+k_4)/6\)の高さは、図では\(y_0\)からの高さとして描かれているので(10)式と同じ意味になります。つまり、この点が\((x_1,y_1)\)ということですね。
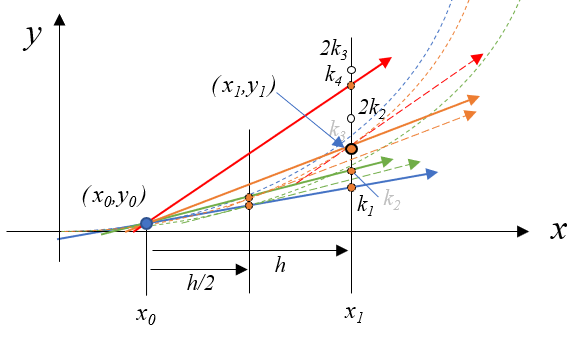
青い破線が理論解の解曲線なので、ルンゲクッタ法で計算するとかなり理論解に近い値が計算できそうですね。
ルンゲクッタ法で数値計算
ルンゲクッタ法の計算はかなり正確に理論解と一致いることが分かります。\(h=0.1\)と計算幅を大きくとっていますが、ずれはすくないですね。
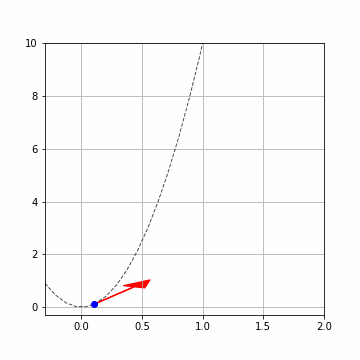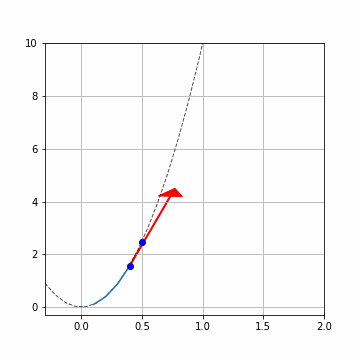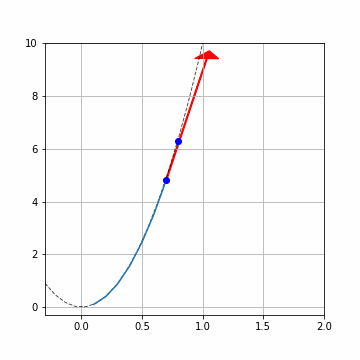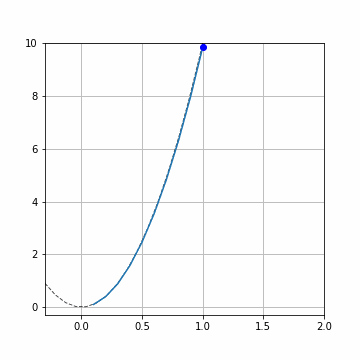
赤い矢印は傾き\(f(x_i,y_i)\)です。青い点で\((x_i,y_i),(x_{i+1},y_{i+1})\)を示しています。
このように、少し先の情報を多く使用することで、精度を上げることが出来ました。
ルンゲクッタ法のプログラム – Python –
# 傾き関数
def dy(x,y):
dy = (2*y/x)
dx = 1
return [dx, dy]
# 初期パラメータ
x0 = 0.1
y0 = 0.1
#数値配列
x_array_rk = [x0]
y_array_rk = [y0]
# ルンゲクッタ法で計算
xp = x0
yp = y0
dl = 0.1
for i in range(100):
x_pn = xp + dl
x_ph = xp + dl/2
k1 = dy(xp, yp)[1] * dl
k2 = dy(x_ph, yp + k1/2)[1]*dl
k3 = dy(x_ph, yp + k2/2)[1]*dl
k4 = dy(x_pn , yp + k3)[1]*dl
x_next = x_pn
y_next = yp + (k1 + 2*k2 + 2*k3 + k4)/6
x_array_rk.append(x_next)
y_array_rk.append(y_next)
xp = x_next
yp = y_next
計算方法の比較
では最後にすべての手法の計算結果を一緒に描いてみます。
オイラー法(Euler)、ホイン法(Heun)、ルンゲクッタ法(Runge-Kutta)に加えて解析解(Analytical)を描くとこのようになります。
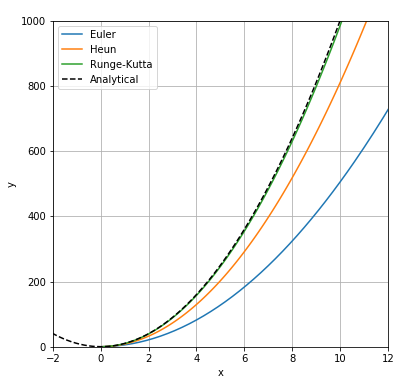
ルンゲクッタ法と解析解はほぼ重なっていることが分かりますね。この比較から、ルンゲクッタ法が最もよく解析解、つまり解曲線を描けているということが分かります。


コメント