フーリエ級数展開の計算で使用される三角関数の直行性についての証明です。丁寧に式を展開して確認してみます。
直交とは
直交とは何かとベクトルで考えてみましょう。
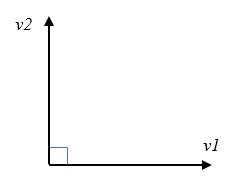
ベクトル \(v1, v2\)は上図のように互いに90°の傾きをもっています。これが、直交している状態ですね。
このとき\(v1,v2\)の内積を計算するとゼロになります。
例えば、\(v1 = [v1_0, v1_1, v1_2]^T, v2=[v2_0, v2_1, v2_2]^T\)とします。すると内積は
$$
(v_1,v_2) = \left[v1_0, v1_1, v1_2 \right] \left[ \begin{array}{c} v2_0 \\ v2_1 \\ v2_2 \end{array} \right] = \sum_{k=0}^{2} v1_k v2_k
$$
のように計算されます。ベクトルの場合は値がとびとびの離散値と考えられるので総和です。そして、値が離散値ではなく連続であると考えると、積分計算によって置き換えることが出来るようになります。
つまり、直交であるとは、二つの関数を積分してときにその結果がゼロになると、その関数は互いに直交しているという事が出来ます。
では実際に三角関数の直交性を計算で確かめてみましょう。
\(\sin\)関数同士の直交性
(1)式を展開することで、\(\sin\)関数同士の直交性を確認することが出来ます。
$$
\int_{-\pi}^{\pi} \sin(mx) \sin(nx) dx \tag{1}
$$
\(m \neq n\)の場合
(1)式を加法定理により変形します。
加法定理より、(1)式は(2)式のように変形できます。
$$
\int_{-\pi}^{\pi} \sin(mx)\sin(nx) dx = \frac{1}{2} \int_{-\pi}^{\pi} \left\{ \cos((m-n)x) – \cos( (m+n) x) \right\} dx \tag{2}
$$
(2)式を積分します。
$$
\int_{-\pi}^\pi \sin(mx) \sin(nx) dx = \frac{1}{2} \left\{ \left[ \frac{1}{m-n} \sin((m-n)x) – \frac{1}{m+n} \sin((m+n)x) \right]_{-\pi}^{\pi} \right\}
$$
ここで\( \sin(k \pi) =0 , k \in \mathbb{N} (自然数の集合)\)より(1)式は(3)式となります。
$$
\int_{-\pi}^{\pi} \sin(mx)\sin(nx) dx = 0 \tag{3}
$$
\( m = n\)の場合
\(m = n\)なので、(4)式の計算を行います。
$$
\int_{-\pi}^\pi \sin(mx) \sin(mx) dx =\int_{-\pi}^\pi \sin^2(mx)dx \tag{4}
$$
ここでも加法定理を少し変形して(4)式を変更するようにします。
加法定理により、(4)式は(5)式になります。
$$
\int_{-\pi}^\pi \sin^2(mx)dx = \frac{1}{2} \int_{-\pi}^{\pi} \left\{ 1 – \cos(2m x) \right\} dx \tag{5}
$$
(5)式を積分していきます。1段目から2段目への計算は\( \sin(k \pi) = 0 , k \in \mathbb{N}(自然数の集合) \)の関係を使用しています。
$$
\begin{eqnarray}
\frac{1}{2} \int_{-\pi}^\pi \left\{ 1 – \cos(2m x) \right\} dx &=&
\frac{1}{2} \left\{ \left[ x – \frac{1}{2m} \sin(2mx) \right]_{-\pi}^{\pi} \right\} \\
&=& \frac{1}{2} \left\{ \pi – (-\pi) \right\} \\
&=& \pi
\end{eqnarray}
$$

\(sin\)関数同士の場合をまとめると
\(m \neq n\)の時はゼロで、\(m = n\)の時は\(\pi\)でした。そこで、\(\delta\)関数を使って表現すると
$$
\int_{-\pi}^{\pi} \sin(mx) \sin(nx) dx = \pi \delta_{m,n} \tag{6}
$$
となります。\(\delta_{m,n}\)は\(m=n\)のとき”1″となり、\(m \neq n\)のとき”0″となる関数です。
この関係から、\(sin(nx), n \in \mathbb{Z} \)は同じ信号同士以外はすべて直交していると言えます。
\(\cos\)関数同士の直交性
(7)式を展開することで、\(\cos\)関数同士の直交性を確認することが出来ます。
$$
\int_{-\pi}^{\pi} \cos(mx) \cos(nx) dx \tag{7}
$$
\(m \neq n\)の場合
加法定理より
$$
\cos(mx) \cos(nx) = \frac{1}{2} \left\{ \cos((m+n)x) + \cos( (m-n) x) \right\}
$$
とすることとが出来ます。これより(7)式は(8)式になります。
$$
\int_{-\pi}^{\pi} \cos(mx) \cos(nx) dx = \frac{1}{2} \int_{-\pi}^{\pi} \left\{ \cos((m+n)x) + \cos( (m-n) x) \right\} \tag{8}
$$
(8)式を積分すると、\( \sin(k \pi), k \in \mathbb{N} (自然数の集合) \)より、結果はゼロになります。
$$
\begin{eqnarray}
\int_{-\pi}^{\pi} \cos(mx) \cos(nx) dx
&=& \frac{1}{2} \left[ \frac{1}{m+n} \sin((m+n)x) + \frac{1}{m-n} \sin( (m-n) x) \right]_{-\pi}^{\pi} \\
&=& 0
\end{eqnarray}
$$
\( m = n\)の場合
\(m = n \)なので、(7)式は(9)式になります。
$$
\int_{-\pi}^{\pi} cos(mx) cos (mx) dx = \int_{-\pi}^{\pi} \cos^2(mx) dx \tag{9}
$$
加法定理を少し変更し、展開します。
これより(9)式は(10)式のようになります。(10)式の2段目から3段目への展開は\( \sin(k \pi) =0 , k \in \mathbb{N} (自然数の集合) \)を適用しています。
$$
\begin{eqnarray}
\int_{-\pi}^{\pi} \cos^2(mx) dx
&=& \frac{1}{2} \int_{-\pi}^{\pi} \left\{ 1 + \cos(2mx) \right\} dx \\
&=& \frac{1}{2} \left[ x + \frac{1}{2m} \sin(2mx) \right]_{-\pi}^{\pi} \\
&=& \frac{1}{2} \left\{ \pi – (-\pi) \right\} \\
&=& = \pi
\end{eqnarray} \tag{10}
$$

\( \cos \)関数同士の場合をまとめると
\(m \neq n\)の時はゼロで、\(m = n\)の時は\(\pi\)でした。そこで、\(\delta\)関数を使って表現すると
$$
\int_{-\pi}^{\pi} \cos(mx) \cos(nx) dx = \pi \delta_{m,n} \tag{11}
$$
となります。\(\delta_{m,n}\)は\(m=n\)のとき”1″となり、\(m \neq n\)のとき”0″となる関数です。
この関係から、\(cos(nx), n \in \mathbb{Z} \)は同じ信号同士以外はすべて直交していると言えます。
\( \sin\)関数と\(\cos\)関数の直交性
(12)式の計算を行うことで、\(\sin\)関数と\(\cos\)関数の直交性を確認することが出来ます。
$$
\int_{-\pi}^{\pi} \sin(mx) \cos(nx) dx \tag{12}
$$
ここで\(\sin\)が奇関数で\(\cos\)が偶関数、そして奇関数と偶関数の掛け算は奇関数になること、さらに奇関数の区間 \([-a, a]\)の定積分がゼロになることから(12)式は(13)式になります。
$$
\int_{-\pi}^{\pi} \sin(mx) \cos(nx) dx = 0 \tag{13}
$$
直交性のまとめ
三角関数の直交性をまとめます。
$$
\int_{-\pi}^{\pi} \sin(mx) \sin(nx) dx = \pi \delta_{m,n}
$$
$$
\int_{-\pi}^{\pi} \cos(mx) \cos(nx) dx = \pi \delta_{m,n}
$$
$$
\int_{-\pi}^{\pi} \sin(mx) \cos(nx) dx = 0
$$
\( m, n \in \mathbb{N}(自然数の集合) \)
$$
\left\{
\begin{array}{l l}
\delta_{m,n} = 1 & m = n \\
\delta_{m,n} = 0 & m \neq n
\end{array}
\right.
$$


コメント