平方根の計算をニュートン法で行ったので、これをもう少し拡張してみます。やることは、3乗根の計算、n乗根の計算、それから方程式の解をニュートン法で求めてみます。
3乗根をニュートン法で求める
3乗根の計算は\(x = C^{1/3}\)を求めるものです。\(C = 8\)とすると、\(x = 2\)ですね。この計算をニュートン法で行ってみます。
まずは\(x^3 = C\)として、関数\(f(x)\)を(1)式とします。
$$
f(x) = x^3 – C \tag{1}
$$
ニュートン法で使用する関数\(f(x)\)の一階微分\(f^\prime(x)\)は(2)式です。
$$
f^\prime(x) = 3x^2 \tag{2}
$$
あとはこの(1)式、(2)式を(3)式のニュートン法で収束させれば解が出ますね。
$$
x_{k+1} = x_k – f(x_k) / f^\prime(x_k) \tag{3}
$$
\(C=8\)として解を計算してみます。
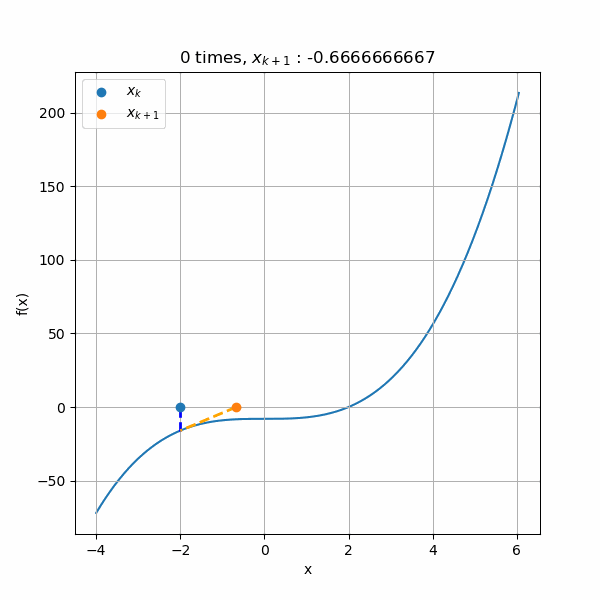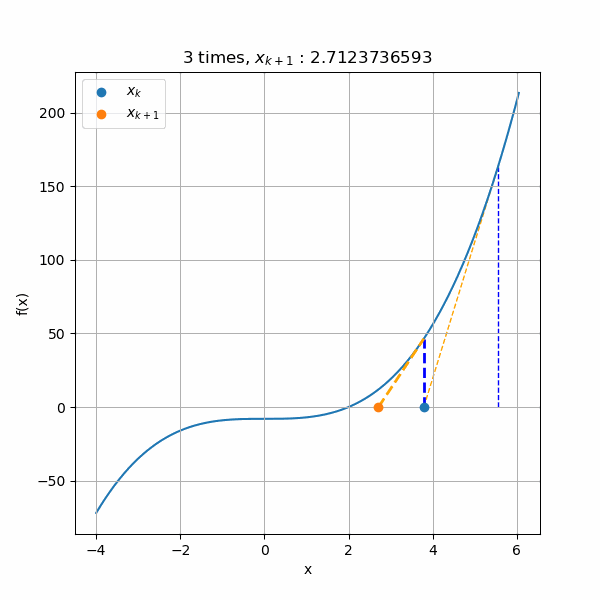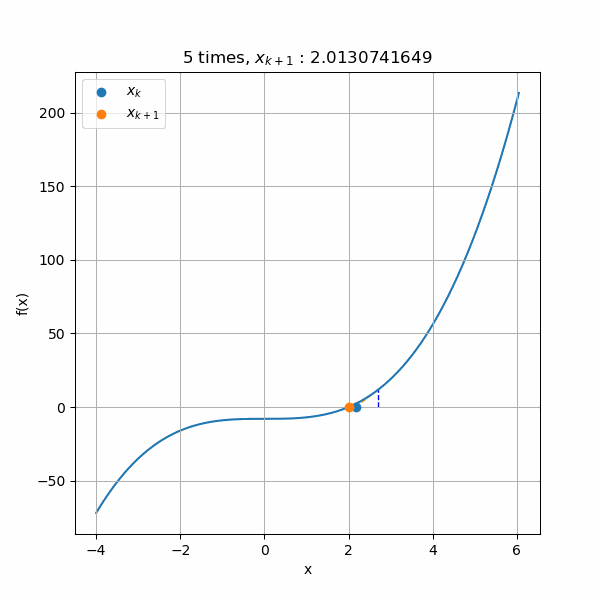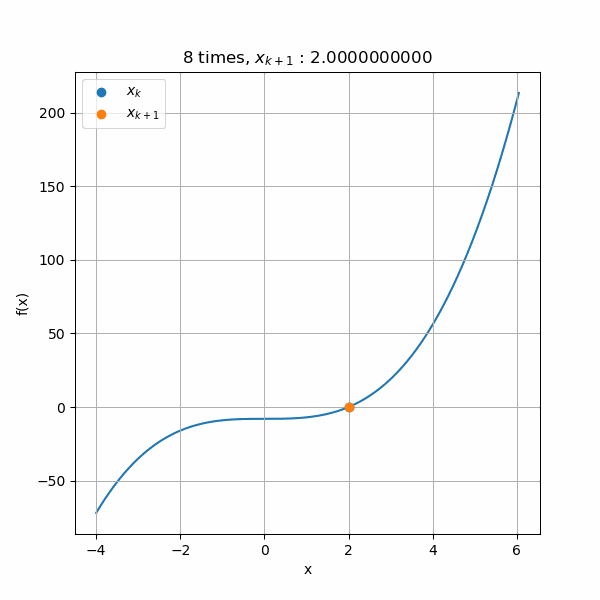
まず、解のプラス側から収束するアニメーションです。初期値を3として計算すると、ちゃんと解の2へ収束していきますね。

次は解のマイナス側から収束させたアニメーションです。初期値を-2として計算しています。こちらも解の2へと収束できていますね。
3乗根を求めるプログラムコード – python
def cubit_root(value, sigma):
# 関数定義
f = lambda x: x**3 - value
df = lambda x: 3*x**2
# 初期値の設定
x0 = 3
# ニュートン法による収束
while True:
x = x0 - f(x0) / df(x0)
if abs(x-x0) < sigma:
break
else:
x0 = x
return x
実行
x = cubit_root(8, 0.0000001) print(x) # 出力 2.0
n乗根をニュートン法で求める
平方根(2乗根)、3乗根をニュートン法で求めたので、n乗根を求めてみます。
同じ考え方でまとめていくと、
n乗根は\(x = C^{1/n}\)を計算するものです。両辺をn乗して\(x^n = C\)として関数\(f(x,n)\)を(4)式とします。
$$
f(x,n) = x^n – C = 0 \tag{4}
$$
そして、\( \partial f(x,n) / \partial x \)は(5)式です。
$$
\partial f(x,n) / \partial x = n x^{n-1} \tag{5}
$$
これを(6)式のニュートン法で収束させます。
$$
x_{k+1} = x_k – f(x_k, n) / \bigl( \partial f(x_k, n) / \partial x \bigr) \tag{6}
$$
n乗根をニュートン法で求めるプログラムコード – Python
n乗根の計算では、関数の引数としてn乗の\(n\)、n乗根を計算する\(value\)、そして収束条件の\(sigma\)を設定します。
root関数内でlambda関数を使い必要な計算を定義できるので、Pythonはフレキシブルな言語ですね。非定常な計算をする場合は特に有効だと感じます。
def root(n, value, sigma):
# 関数定義
f = lambda x: x**n - value
df = lambda x: n*x**(n-1)
# 初期値の設定
x0 = 1
# ニュートン法で解を計算
while True:
x = x0 - f(x0) / df(x0)
if abs(x-x0) < sigma:
break
else:
x0 = x
return x
実行
# 2の4乗根の計算 x = root(4,2,0.00001) print(x) # 出力 1.1892071156761177 # 32の5乗根の計算 x = root(5,32, 0.0001) print(x) # 出力 2.0000000000000244
以上でn乗根の計算ができました。結構簡単ですね。
方程式の解をニュートン法で求める
n乗根をニュートン法で計算できたので、もう少し複雑な方程式の解を求めてみます。
方程式の解を求めるプログラム関数 – Python
まず方程式をニュートン法で求める”solve”という関数をPythonで定義します。これまでのn乗根の関数との違いは、方程式\(f\)とその微分\(df\)を関数の引数に設定しているところで。これで、どんな関数が来てもニュートン法で解を求めることが出来ます。初期値\(initial_x\)により収束する解が変わりますが、これは手動で設定するようにします。
それから、収束しないことも考えられるので、収束回数には上限を設けるようにしています。
def solve(initial_x, f, df, sigma):
# 初期値の設定
x0 = initial_x
# 収束回数のカウント
i = 0
# ニュートン法による解の探索
while True:
i = i + 1
x = x0 - f(x0)/df(x0)
if abs(x - x0) < sigma:
break
else:
x0 = x
# 収束回数の上限
if i > 20 :
break
return x
方程式: \(f(x) = (x-1)^2 = 0\)の解
まずは簡単な\((x-1)^2 = x^2 -2 x +1 = 0\)の解をニュートン法で求めます。解は\(+1\)になるはずですね。
実装する関数を(7)式として、計算を実行します。
$$
\begin{eqnarray}
f(x) &=& x^2 -2x+1 \\
f^\prime(x) &=& 2x -2
\end{eqnarray} \tag{7}
$$
#関数定義 f = lambda x : x**2 -2 *x +1 df = lambda x : 2*x - 2 # 収束条件定義 sigma = 0.0000001 #初期値設定 initial_x = -3 # ニュートン法で解を計算 solve(initial_x, f, df, sigma) # 出力 : 0.9999980926513672
結果が\(0.9999980926513672\)なので、解は求められたとしていいですね。
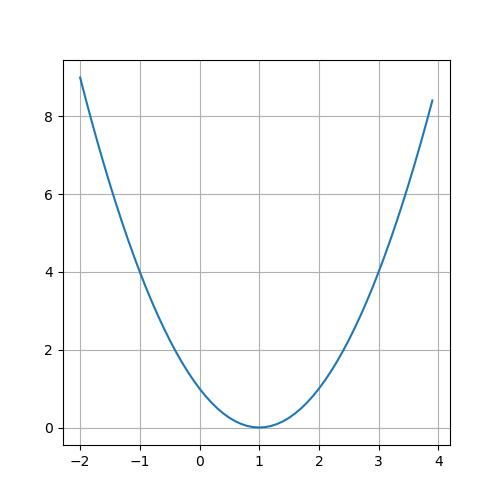
確認のため\(f(x)\)の図を描くと、\(f(x) = 0\)の点が\(x=1\)であることが分かります。
方程式:\(f(x) = (x-1)(x-9) = 0\)の解
次の方程式の解は\(1 , 9\)の二つです。
実装する関数を(8)式として計算を実行します。
$$
\begin{eqnarray}
f(x) &=& x^2 -10 x +9 \\
f^\prime(x) &=& 2x – 10
\end{eqnarray} \tag{8}
$$
# 関数定義 f = lambda x : x**2 -10 *x +9 df = lambda x : 2*x - 10 # 収束条件設定 sigma = 0.0001 #### -----1つ目------ #### # 初期値設定 initial_x = 2 # ニュートン法で解を計算 solve(initial_x, f, df, sigma) # 出力 : 0.9999999999997591 #### -----2つ目------ #### # 初期値設定 initial_x = 8 # ニュートン法で解を計算 solve(initial_x, f, df, sigma) # 出力 : 9.000000000000242
初期値\(initial_x\)を変更することで(\(0.9999999999997591, 9.000000000000242\))と解が求められました。
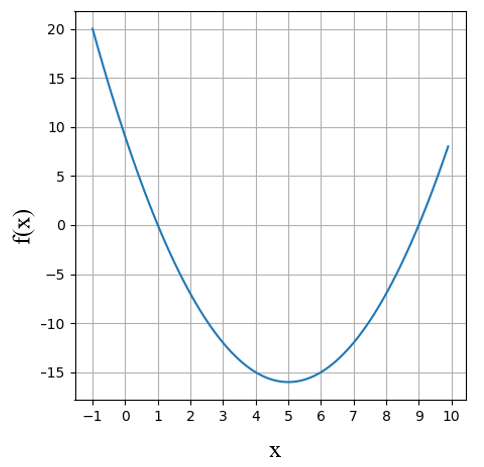
確認のため\(f(x)\)の図を描くと、\(f(x) = 0\)の点は\(1\)と\(9\)であることが分かります。
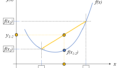
ゼロと交差しない方程式:\(f(x) = (x-1)^2 + 4\)の場合
これまでは関数がゼロを交差していた場合でした。では、ゼロと交差しない次のような関数の形の場合は、ニュートン法で計算するとどうなるのでしょうか?

これは実際(9)式の関数をニュートン法で計算すると、
$$
\begin{eqnarray}
f(x) &=& x^2 -2 x +5 \\
f^\prime(x) &=& 2x – 2
\end{eqnarray} \tag{9}
$$
このような形となり、いつまでも収束できません。

ということで、ニュートン法で解を求める場合、関数の形に注意することが必要です。
まとめ
ニュートン法を使っていろいろ方程式の解を求めてみました。
方程式の形がゼロと交差する場合はニュートン法が有効です。それから、解が多数ある場合、初期値によりどの解へ収束するかが変化しました。
ニュートン法はほかにも色々な方法があるようなので、そのあたりも勉強してみようと思います。
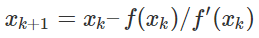
コメント