前回の1変数の勾配法を多変数の関数に適用する場合を考えます。内容は引き続き ”これなら分かる最適化数学, 金谷健一” から引用します。
多変数の勾配法の考え方
1変数の関数\(y=f(x)\)の場合、山を登るように\(x\)の値を変更しますが、これを多変数に当てはめるにはどうすればいいのでしょうか。本の多変数の勾配法のアルゴリズムでは、”\(F(t) = f(x + t \nabla f(x)) \)に対して勾配法を適用する”とあります。
この意味は、多変数\(\boldsymbol x : (x_1, \cdots , x_n) \) で定義された関数\(f (\boldsymbol x) \)を\(t\)という1変数で置き換えた\(F(t) = f(\boldsymbol x + t \nabla f( \boldsymbol x ))\)を定義し、これに対して勾配法を実施することを意味しています。
たとえば、2変数関数 \(f(x,y)\)を考えた場合、\(\nabla f = ( \partial f / \partial x, \partial f / \partial y) \)なので、\(F(t) = f(x + t \partial f / \partial x , y + t \partial f / \partial y)\) のような関数を \(t \)で再定義することになるます。
これを図で表すと、\( \nabla f \)は関数のある点の勾配方向であるので、下の図のように点\( (x_k, y_k) \)の場合は\( \nabla f_k \)の方向となります。\( \nabla f_k \)に \( t \)を掛けると 点\( (x_k, y_k) \) から出発した矢印\( \nabla f_k \) が\( t \)だけ伸びていくことになります。 この方向へ探索を行うと、最大値で次の点 \( (x_{k+1} , y_{k+1}) = (x_k, y_k) + (\Delta x_x, \Delta x_y) \)となります。
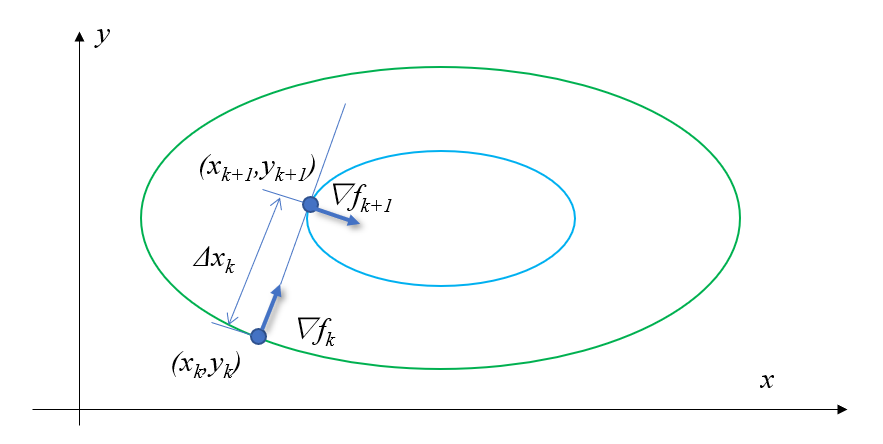
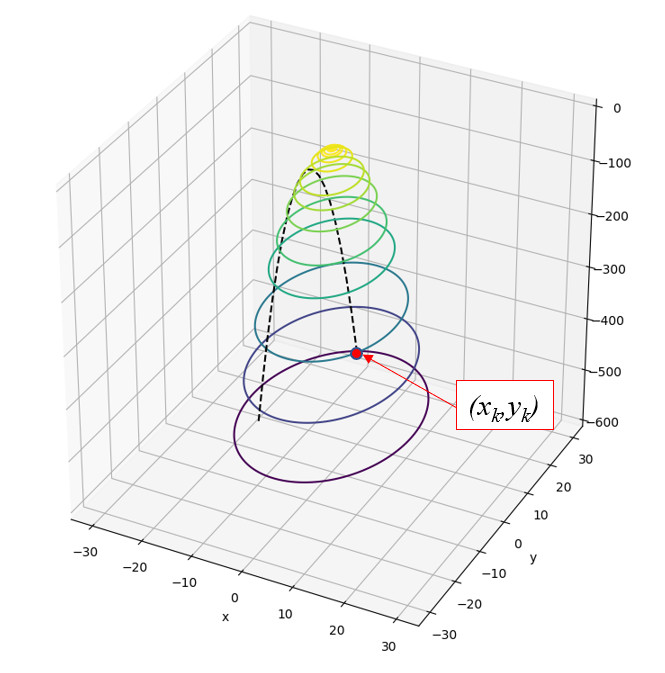
ところで、\( \nabla f \)の方向の最大値がどうして求まるのかというと、関数を\( \nabla f \)の方向に移動させると、下の図の点線のように放物線となるからです。点 \((x_k, y_k) \)の等高線から出発すると、上の黄色い等高線に接する点で最大値となっていることが分かりますね。
実際の関数へ勾配法を適用
では実際に関数\(f (x, y) \)を(1)式として定義して、初期の\( \boldsymbol x_0 \)を\( (-3, -6.5) \)として勾配法を実行してみます。
$$ f(x,y) = -5 (x – 1)^2 – 2 (y – 2)^2 \tag 1$$
関数を等高線で表して、そこで勾配法で最大値を求めると以下のように、等高線の法線方向に、次の等高線と接するまで点を探し、その点からまた等高線の法線方向に次の等高線と接するまで点を探すということを繰り返しながら最大値を探していることが分かります。
収束条件の \( |\Delta x | < \sigma \) は、下の図の各点の間隔がどこかで \( \sigma \)未満となることを意味しています。
ちなみに(1)式の極値は\( (1, 2) \)なので、勾配法でちゃんと求まっていますね。
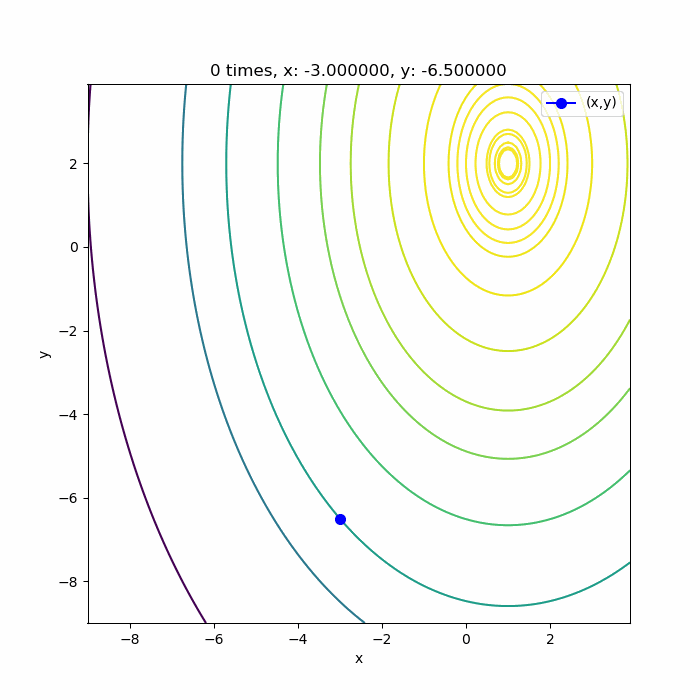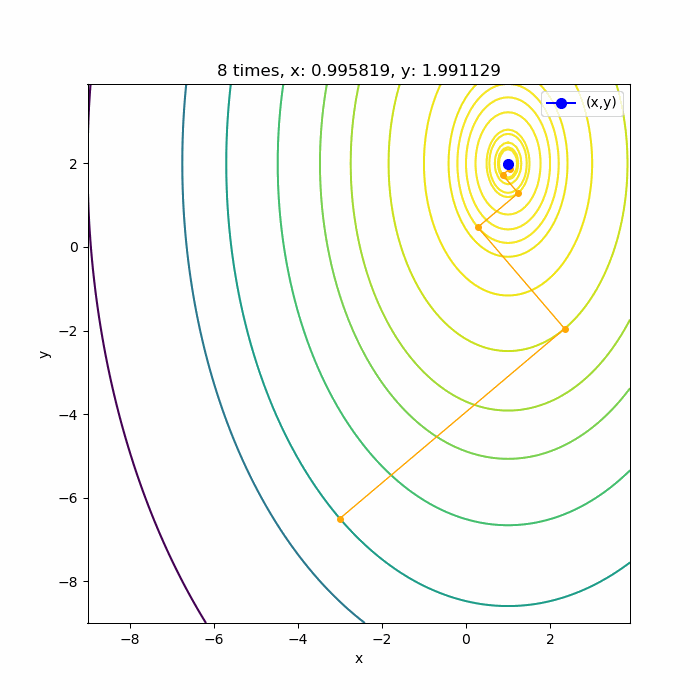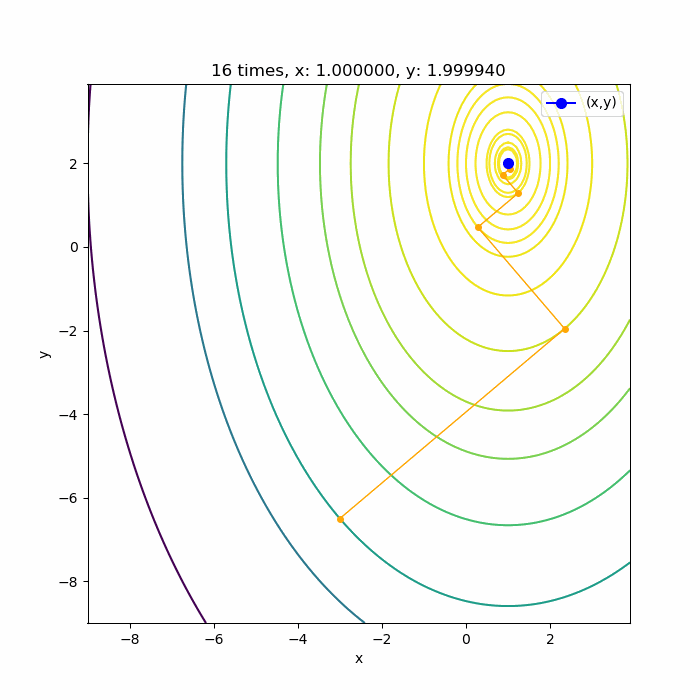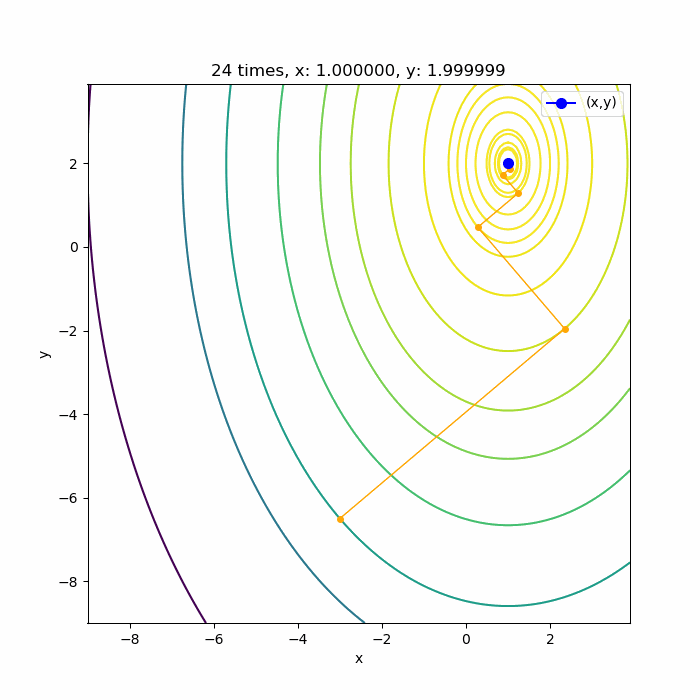
勾配法はこの結果のように、ガタガタ進んでいくことが特徴です。場所が悪いと上の結果のように収束まで時間がかかってしまいます。
次は収束が早いニュートン法について記事にします。
今回使用した多変数の勾配法プログラムコード
1変数の勾配法 クラス
class Search(object):
def __init__(self, func):
# f : function
self.func = func
def diff_func(self, t): #関数の微分を中心差分で求める
delta_h = 0.000001
return (self.func(t + delta_h) - self.func(t - delta_h) ) / ( 2* delta_h)
def search_max(self, initial_t, initial_h, epsiron):
# step 1 : 初期値の設定
t = initial_t
h = initial_h
while abs( self.diff_func(t) ) > epsiron : # step 5 : 収束のチェック
# step 2
h = np.sign( self.diff_func(t) ) * abs(h)
T = t
Td = t + h
if self.func(T) < self.func(Td): # step 3
while self.func(T) <= self.func(Td): # step 3 (a)
h = 2*h
T = Td
Td = T + h
# step 3 (b)
t = T
h = h /2
else: # step 4
while self.func(T) >= self.func(Td): # step 4 (a)
h = h / 2
Td = Td - h
# step 4 (b)
t = Td
h = 2 * h
return t
2変数の勾配法 クラス
class Hill_Climb(object):
__delta_h = 0.000001
def __init__(self, func):
self.func = func
def diff_x_func(self, x, y): ## x軸方向への偏微分
return ( self.func( x+self.__delta_h ,y ) - self.func( x-self.__delta_h ,y ) ) / (2*self.__delta_h)
def diff_y_func(self, x, y): ## y軸方向への偏微分
return ( self.func( x, y+self.__delta_h ) - self.func( x, y-self.__delta_h ) ) / (2*self.__delta_h)
def value_of_x(self, x, y):
return np.sqrt(x**2 + y**2)
def hill_climb_max(self, initial_x, initial_y, sigma):
x = initial_x
y = initial_y
while True:
## 関数 F(t) の定義
func = lambda t : self.func( x + t * self.diff_x_func(x, y), y + t * self.diff_y_func(x, y))
## 1変数の勾配法
search = Search(func)
## 最大値 t の探索
initial_t = 0.1 ## 初期値は常に0.1から始める
initial_h = 0.1 ## 初期のステップ幅
epsiron = 0.00001 ## 収束判定
max_t = search.search_max(initial_t, initial_h, epsiron)
## delta_xの計算
delta_x_x = max_t * self.diff_x_func(x, y)
delta_x_y = max_t * self.diff_y_func(x ,y)
## xの更新
x = x + delta_x_x
y = y + delta_x_y
if self.value_of_x(delta_x_x, delta_x_y) < sigma:
break
return (x,y)
実行プログラムコード
# 関数の設定 function = lambda x,y : -5*(x-1)**2 - 2*(y-2)**2 # 初期値の設定 initial_x = -3 initial_y = -6.5 delta = 0.000001 #収束条件 # hill_climeの設定 hill_climb = Hill_Climb(function) ## 最大値探索 max_x = hill_climb.hill_climb_max(initial_x, initial_y, delta) ## 最大値 print(max_x)
コメント