機械学習の理解のため、 ”これなら分かる最適化数学, 金谷健一”を勉強中です。ここではニュートン法を勉強して、理解したことをまとめます。
ニュートン法のアルゴリズム概要
ニュートン法は勾配法に比べてとても綺麗に考えられた方法です。学生の時にBasicで何だか分からずにプログラムをコーディングしたことがありましたが、金谷先生の本で勉強するとなるほどとすんなり理解できました。卒業してからも勉強を続ける事って面白いですね。
まず、点\( \bar x _k \)で関数\(f\)をテーラー展開し、3次以上を無視すると、2次近似 \( f_{II k}\) (1)式になります。この式は\( \Delta x \)が変数となっているので、\( \Delta x \)で微分した式 を \( 0 \) とおく( (2)式 )、極値(極大 または極小)の点が求まります。
$$
f_{II k} = f(\bar x) + f^{\prime} (\bar x) \Delta x + \frac{1}{2} f^{\prime \prime}(\bar x) \Delta x ^2 \tag{1}
$$
$$
f^{\prime} (\bar x) + f^{\prime \prime}(\bar x) \Delta x = 0 \tag{2}
$$
(2)式を\( 0 \)とするには、\(f^{\prime}(\bar x), f^{\prime \prime}(\bar x) \)は定数なので、\( \Delta x \)だけが変数項です。よって(3)式の\( \Delta x \)が(2)式を\( 0\)とする値です。
$$
\Delta x = – \frac{f^{\prime}(\bar x)}{f^{\prime \prime} (\bar x)} \tag{3}
$$
これを今の順番に絵を描くと、こんな感じですね。ニュートン法は勾配法と同じく何度か繰り返して極値を求める方法です。今 \(k\)回目だとすると、\(\bar x_k\) でテーラー展開された \( f_{II k}\) の極値\(x_k\)は\( \bar x_k \)に\(\Delta x_k \)を加えることで求まります。
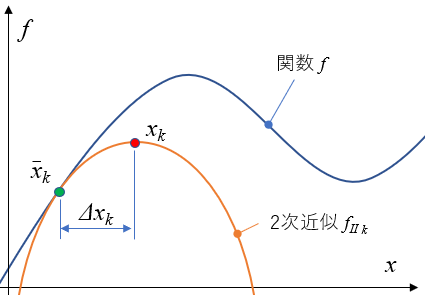
そして次の\(k+1\)回目は、前回求めた\( x_k\)を次のテーラー展開の点\( \bar x_{k+1} \)とし、 \( f_{II k+1}\) の極値 \(x_{k+1} \)を \( \bar x_{k+1} \) と\( \Delta x_{k+1} \)から求めます。
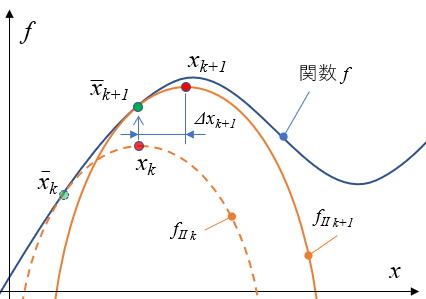
これを\( |\Delta x | < \sigma \)になるまで繰り返せば、関数 \(f \)の極値を求めることができます。とても綺麗なアルゴリズムですよね。特に、関数\(f\)を2次近似することで、必ず極値が求まるようにしているところが綺麗ですよね。
数値計算
ではニュートン法を実行してみます。適用する関数は(4)式の3次関数です。
$$
f(x) = x^3 – 2x^2 + x + 3 \tag{4}
$$
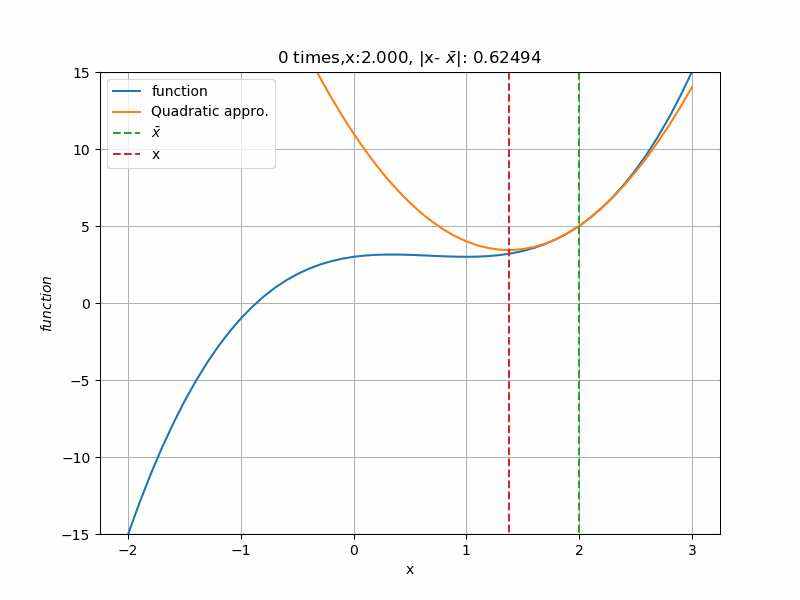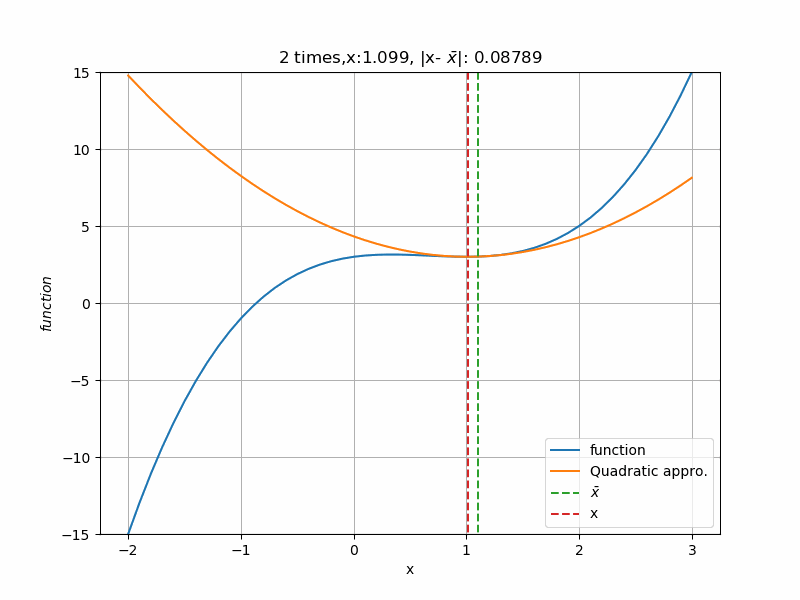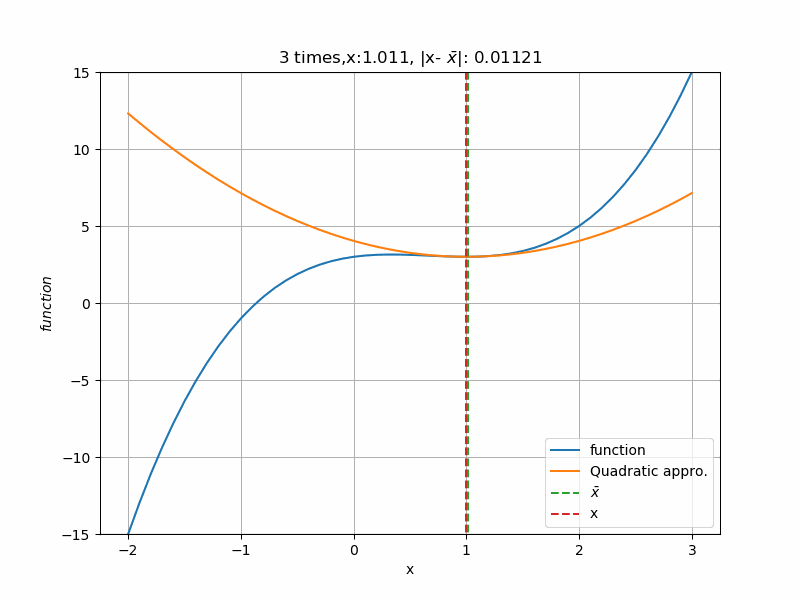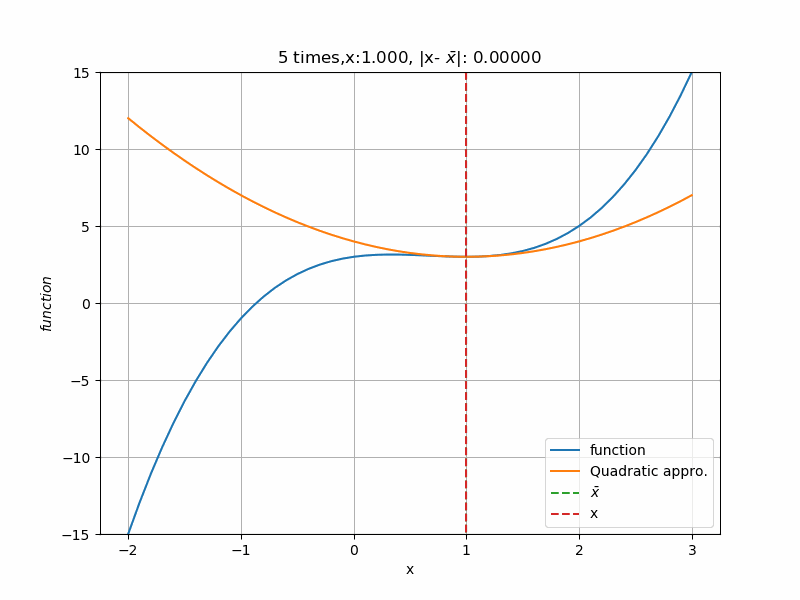
初期値\(2.5 \)から計算すると、次のように収束していきます。青線:functionが(4)式、橙線:Quadratic approc.が\(\bar x\)での2次近似式です。回数を重ねる毎に2次近似の形が変わり、関数の極値\(1 \)に近づいていきます。近づく毎に、2次近似の形が緩やかになっていることが分かりますね。これは、極値へ近づくにつれて関数の形がフラットに近づいているからです。勾配法とは違い、次の点(この場合\(k+1\)回目の\(\bar x_{k+1}) \)は一回の計算で済むので、収束にかけある計算回数がとても速いです。
初期値を\(-1.5\)から始めた場合、次のように収束します。さっきと違い、2次近似が上に凸の形になっていますね。収束する側に合わせて2次近似の形が決まっています。
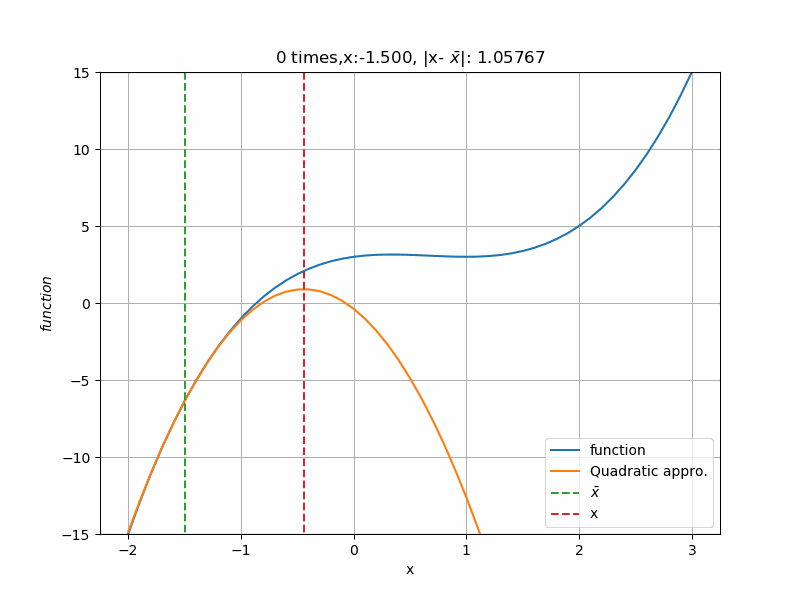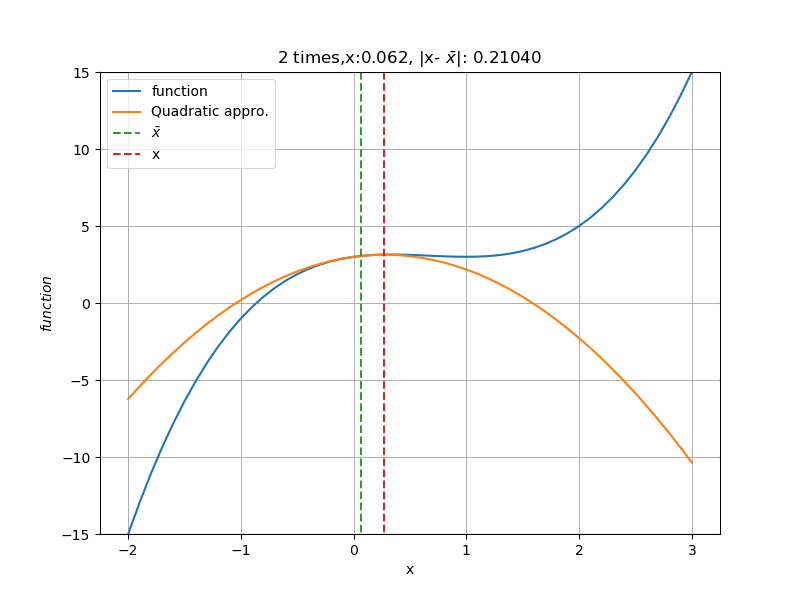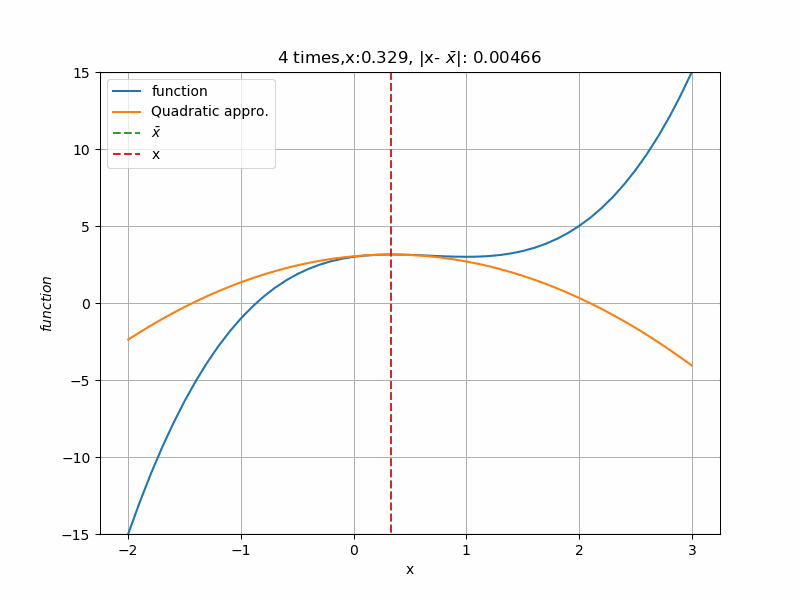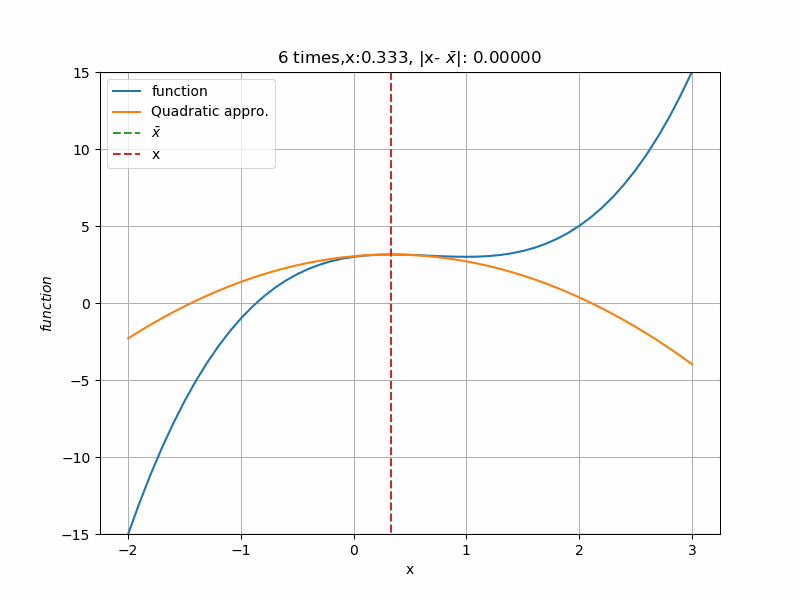
ということで、1変数のニュートン法でした。次は多変数の場合のニュートン法を記事にします。
ニュートン法のコード – Python
ニュートン法のコードです。Pythonで書くと引数に関数(lambda)を設定できるので、思考がそのまま実装できるので楽ですね。Basicでコーディングした時とはだいぶ違うなぁ。
ニュートン法のクラス
class Newton(object):
def __init__(self, function):
self.func = function
self.delta_h = 0.000001
def d_func(self, x): # 中心差分
return (self.func(x + self.delta_h) - self.func(x - self.delta_h)) / (2 * self.delta_h)
def dd_func(self, x): # 中心差分の中心差分
return (self.d_func(x+self.delta_h) - self.d_func(x-self.delta_h)) / (2 * self.delta_h)
def search(self, initial_x, sigma): # ニュートン法のイテレーション
x = initial_x
while True:
x0 = x
delta_x = - self.d_func(x0)/self.dd_func(x0)
x = x0 + delta_x
if abs(x-x0) < sigma:
break
return x
実行
# 関数の設定 f = lambda x : x**3 - 2*x**2 + x + 3 # 初期値の設定 initial_x = 2.5 sigma = 0.000001 #ニュートン法のインスタンス生成 newton = Newton(f) # ニュートン法実行 X = newton.search(initial_x, sigma) print(X) # 結果 : 1.0000
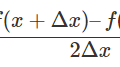

コメント