 数値計算
数値計算 Pythonで離散時間フーリエ変換を実装
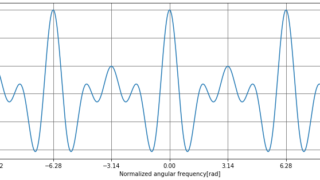
離散時間フーリエ変換の計算式はシンプルです。これをPythonで実装して計算してみます。計算は複素数を使用するので、この扱い方も含めて関数化します。
 数値計算
数値計算  環境設定
環境設定  数値計算
数値計算  数値計算
数値計算 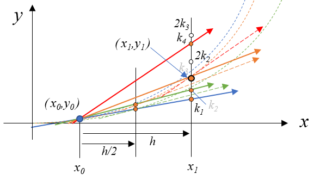 数値計算
数値計算 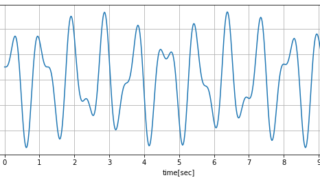 数値計算
数値計算 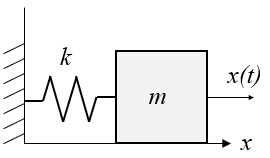 数値計算
数値計算 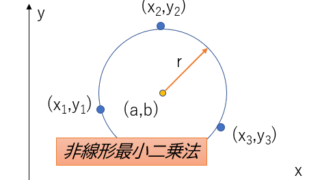 数値計算
数値計算  数値計算
数値計算  数値計算
数値計算