 数値計算
数値計算 色々な離散データの離散時間フーリエ変換を計算してみる
色々な離散データの離散時間フーリエ変換をpythonで計算してみます。三角関数、インパルス、数列の変換と逆変換の図をたくさん載せてます。
 数値計算
数値計算 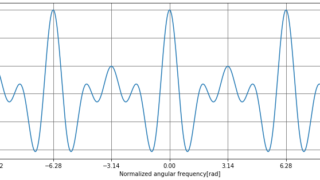 数値計算
数値計算  数値計算
数値計算  数値計算
数値計算 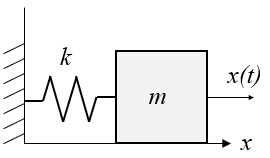 数値計算
数値計算 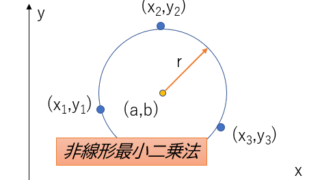 数値計算
数値計算 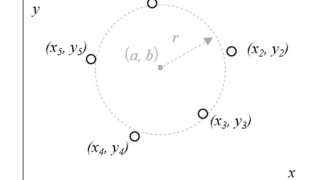 数値計算
数値計算  数値計算
数値計算  機械学習
機械学習  数値計算
数値計算