 数値計算
数値計算 非線形最小二乗法で円のパラメータ推定
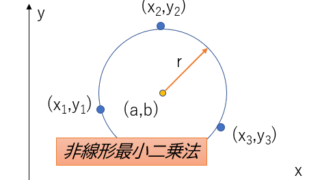
非線形最小二乗法を使って円のパラメータを求めてみましょう。最適化計算における線形、非線形とは何なのか、円の方程式 \( (x-a)^2 + (y-b)^2 = r^2\)のパラメータ\((a,b,r)\)を非線形最小二乗法で求めるとは何なのかといったことを考えながら進めてみます。ちなみに、収束計算はニュートン法で行いますよ。
 数値計算
数値計算 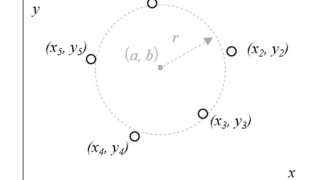 数値計算
数値計算 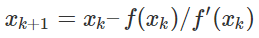 数値計算
数値計算 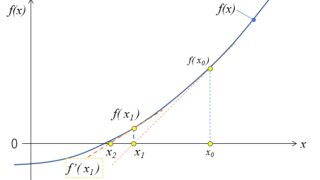 数値計算
数値計算  環境設定
環境設定  数値計算
数値計算  数値計算
数値計算  数値計算
数値計算  数値計算
数値計算