 数値計算
数値計算 多変数のニュートン法の収束の様子を可視化
” これなら分かる最適化数学, 金谷健一 “の ニュートン法を多変数関数に適用して極値を探してみます。1変数のニュートン法は綺麗に収束していきましたが、多変数だとどうなるでしょうか。
多変数の場合のニュートン法アルゴリズム
...
 数値計算
数値計算 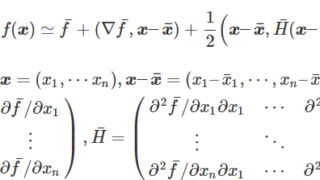 数値計算
数値計算 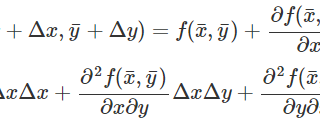 数値計算
数値計算 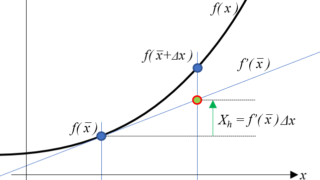 数値計算
数値計算