 数値計算
数値計算 1階常微分方程式の数値解-オイラー法、ホイン法、ルンゲクッタ法
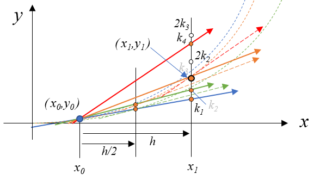
1階常微分方程式の解曲線を数値計算で求めてみます。解曲線とは微分方式の解\(y(x) = \phi(x)\)が表す曲線のことをいい、この曲線を勾配によって描くことで、微分方程式の解を数値計算で求めることが出来ます。オイラー法、ホイン法、ルンゲクッタ法の3つを図解しながらPythonで計算させてみます。
 数値計算
数値計算  数値計算
数値計算  数値計算
数値計算  数値計算
数値計算  数値計算
数値計算  数値計算
数値計算  数値計算
数値計算 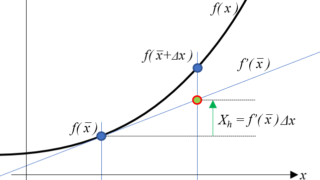 数値計算
数値計算 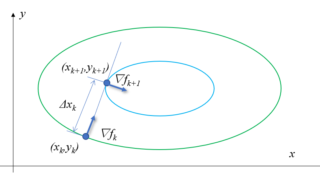 数値計算
数値計算 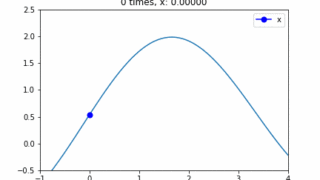 数値計算
数値計算