補間とは何か
ある時間毎にデータをサンプリングした時に、そのサンプリング点に当てはめることが出来る式を探し、サンプリングしていない点を計算で求めることを補間といいます。
例えば、ある時間毎\(x_i,(i = 1,2,\cdots,n)\)に距離データを\(f_i (i=1,2,\cdots,n) \)で取得出来たとします。
この時に言えるのは、例えば「\(x_1\)では\(f_1\)である」といった、計測したことです。データとデータの間の値や、測定した範囲外の値はデータから推定するしかありませんね。
そこで、その点にマッチするように、ある関数\(f(x)\)を点へ当てはめてしまえば、任意の時間における距離のデータを推定することができます。
当てはめる式の形を決めてしまえば、最小二乗法を適用することが出来ます。例えば、幾つか取得したデータに「円の式」を当てはめるなどですね。
この記事では、補間する式の形を考えないで、データから補間式を作成するラグランジュの補間公式を紹介します。
ラグランジュの補間公式
ラグランジュの補間公式は、最小二乗法とは違い、補間する式の形を考えないで、得られたデータから補間する式を自動的に作成する方法です。
最小二乗法との違い
何を言っているかというと、式をデータに当てはめる最小二乗法では、最初に当てはめる式を考えて、その式をデータからずれが最も少なくなるように式のパラメータを決める方法です。
例えば、「データに直線(\(f(x) = ax + b\))を当てはめる」といったことを行います。
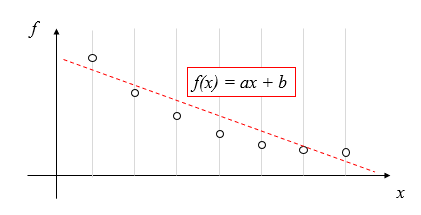
これは、上の図のように “〇” で表されている得られたデータ( \(x_i, f_i, (i=1,2,\cdots, n ))\)に合う、直線の式 \((f(x) = ax + b)\)のパラメータ\(a\)と\(b\)を求める方法です。
最小二乗法で式のパラメータを求めることは、\( A x = b\)の一般逆行列を解くことと同義と考えることが出来ます。
例えば、データが\( (x_0, f_0), (x_1, f_1), (x_2, f_2) \)と取得出来た場合、これを直線の式に当てはめて、\( A x = b\)の形にすると(1)式になるので、
$$
\begin{eqnarray}
a x_0 + b &=& f_0 \\
a x_1 + b &=& f_1 \\
a x_2 + b &=& f_2
\end{eqnarray}
\Rightarrow
\left(\begin{array}{c c}
x_0 & 1 \\
x_1 & 1 \\
x_2 & 1
\end{array}\right)
\left(\begin{array}{c}
a \\ b
\end{array}\right)
=
\left(\begin{array}{c}
f_0\\
f_1\\
f_2
\end{array}\right) \tag{1}
$$
この(1)の関係から、一般逆行列を解けば\(x = (a \quad b)^T\)を求めることが出来ます。
ラグランジュの補間公式の定義
まずは数式です。
関数\(f(x)\)を\(x_i ( i = 1,2,\cdots,n) \)でサンプリングしたデータ \( f_i ( i = 1,2,\cdots,n) \)とします。この\(f(x)\)は\(x_iとf_i\)を用いてラグランジュの補間公式\(p_n(x)\)で近似することが出来ます。
$$f(x) \simeq p_n(x) = \sum_{i=0}^{n} L_i(x) f_i \tag{2}$$
$$L_i(x) = \prod_{k=0, k\neq i}^{n} \frac{x-x_k}{x_i-x_k} \tag{3} $$
(3)式の\(L_i(x)\)はラグランジュの補間係数関数で、例えば\(i=2\)の時は以下のように展開されます。このように展開されることで、分母の項がゼロにならないように調整されます。
$$
L_2(x) = \frac{(x-x_0)(x-x_1)(x-x_3)(x-x_4)\cdots(x-x_n)}{(x_2-x_0)(x_2-x_1)(x_2-x_3)(x_2-x_4)\cdots(x_2-x_n)}
$$
ラグランジュ補間公式の意味
サンプリング点を\(x_i = (x_0,x_1,x_2)\)、そしてその時のデータ点を\(f_i = (f_0,f_1,f_2)\)として、具体的に値を計算してラグランジュ補間公式の意味を考えてみます。
まず、これらの点を用いて、ラグランジュ補間公式\(p_n(x)\)を完成させると(4)式になりますね。
$$
\begin{eqnarray}
p_n(x) &=& L_0(x) f_0 + L_1(x) f_1 + L_2(x) f_2 \\
&=& \frac{(x – x_1)(x – x_2)}{(x_0 – x_1)(x_0 – x_2)} f_0 + \frac{(x – x_0)(x – x_2)}{(x_1 – x_0)(x_1 – x_2)} f_1 + \frac{(x – x_0)(x – x_1)}{(x_2 – x_0)(x_2 – x_1)} f_2
\end{eqnarray} \tag{4}
$$
この式の形から、\(L_i(x)\)の分子が\(x^2\)となっているので、2次の式だということが分かります。
この(4)式にサンプリング点\((x_i , i = 1,2,3)\)を代入していきます。
\(x_0\)の代入
\(p_n(x_0)\)を計算します。
$$
\begin{eqnarray}
p_n(x_0) &=& \frac{(x_0 – x_1)(x_0 – x_2)}{(x_0 – x_1)(x_0 – x_2)} f_0 + \frac{(x_0 – x_0)(x_0 – x_2)}{(x_1 – x_0)(x_1 – x_2)} f_1 + \frac{(x_0 – x_0)(x_0 – x_1)}{(x_2 – x_0)(x_2 – x_1)} f_2 \\
&=& f_0
\end{eqnarray}
$$
2項目、3項目の分子には\((x_0 – x_0)\)が存在するので、この項はゼロになることが分かります。
また、1項目は分子=分母となるので、最終的に\(p_n(x_0) = f_0\)となりますね。
\(x_1\)の代入
\(p_n(x_1)\)を計算します。
$$
\begin{eqnarray}
p_n(x_1) &=& \frac{(x_1 – x_1)(x_1 – x_2)}{(x_0 – x_1)(x_0 – x_2)} f_0 + \frac{(x_1 – x_0)(x_1 – x_2)}{(x_1 – x_0)(x_1 – x_2)} f_1 + \frac{(x_1 – x_0)(x_1 – x_1)}{(x_2 – x_0)(x_2 – x_1)} f_2 \
&=& f_1
\end{eqnarray}
$$
1項目、3項目の分子には\((x_1 – x_1)\)が存在するので、この項はゼロになることが分かります。
また、2項目は分子=分母となるので、最終的に\(p_n(x_1) = f_1\)となりますね。
\(x_2\)の代入
\(p_n(x_2)\)を計算します。
$$
\begin{eqnarray}
p_n(x_2) &=& \frac{(x_2 – x_1)(x_2 – x_2)}{(x_0 – x_1)(x_0 – x_2)} f_0 + \frac{(x_2 – x_0)(x_2 – x_2)}{(x_1 – x_0)(x_1 – x_2)} f_1 + \frac{(x_2 – x_0)(x_2 – x_1)}{(x_2 – x_0)(x_2 – x_1)} f_2 \
&=& f_2\end{eqnarray}
$$
1項目、2項目の分子には\((x_2 – x_2)\)が存在するので、この項はゼロになることが分かります。
また、3項目は分子=分母となるので、最終的に\(p_n(x_2) = f_2\)となりますね。
ラグランジュ補間公式の意味
以上の結果から、ラグランジュ補間公式は次の意味を持つことが言えます。
- 使用するデータの点数により、近似式\(p_n(x)\)の形が決まる。
データの点数が\(n\)なら、近似式は\(n-1\)次式になる。 - 近似式\(p_n(x)\)は、その式を構成する\((x_i, f_i)\)を必ず通る。
式の形を考えてから測定データに当てはめる最小二乗法とは違いますよね。
データ点数による補間の違い
ラグランジュ補間公式は、データ点数が\(n\)なら、近似式は\((n-1)\)次式になります。これを実際に計算してみます。
補間される関数\(f(x)\)
補間される関数\(f(x)\)は(5)式とします。この\(f(x)\)から\(x_i\)に対する\(f_i\)を取得し、ラグランジュの補間公式\(p_n(x)\)を作成します。
$$f(x) = 4x^3 -5x^2 +7x^1 + x^0 \tag{5}$$
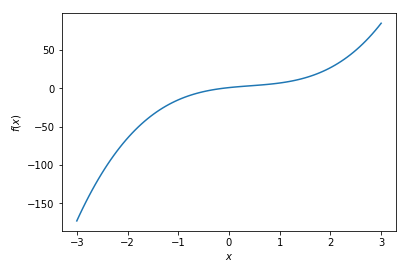
データ点数 \(n=2\)の場合
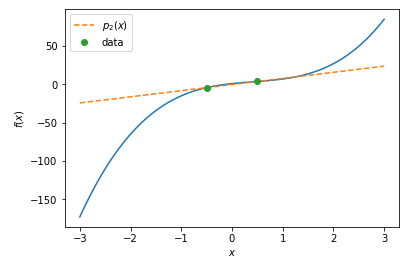
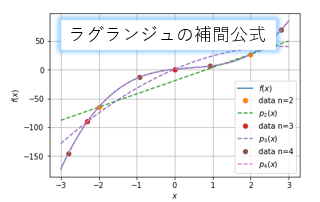
データを二つ \((x_0, f_0), (x_1, f_1)\)使用してラグランジュの補間公式 \(p_2(x)\)を計算すると、以下の図のように直線の近似式になります。\(p_2(x)\)はデータを通っていることが分かりますね。
データ点数 \(n=3\)の場合
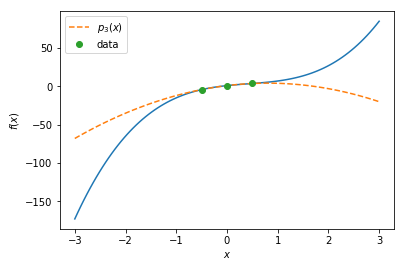
データを三つ \((x_0, f_0), (x_1, f_1), (x_2, f_2)\)使用してラグランジュの補間公式 \(p_3(x)\)を計算すると、以下の図のように2次の近似式になります。\(p_3(x)\)はデータを通っていることが分かりますね。
データ点数 \(n=4\)の場合
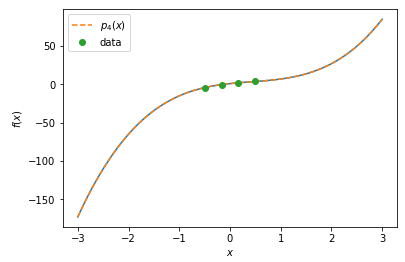
データを四つ \((x_0, f_0), (x_1, f_1), (x_2, f_2), (x_3, f_3)\)使用してラグランジュの補間公式 \(p_4(x)\)を計算すると、以下の図のように3次の近似式になります。\(p_4(x)\)の次数は(5)式の補完される関数\(f(x)\)と同じ次数なので、まったく同じ形をしています。
また、一部の区間だけのデータですが、このデータを使った近似式\(p_4(x)\)はほかの区間でも、\(f(x)\)を近似できています。
データ点数 \(n=5\)の場合
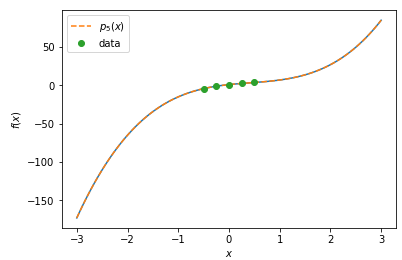
念のため、データを五つ \((x_0, f_0), (x_1, f_1), (x_2, f_2), (x_3, f_3), (x_4, f_4)\)使用してラグランジュの補間公式 \(p_5(x)\)を計算すると、以下の図のように4次の近似式になります。\(p_5(x)\)の次数は(5)式の補完される関数\(f(x)\)と同じ次数ではないですが、まったく同じ形をしています。上位の次数であれば、補間できるということですね。つまり、データがあればあるほど良いと言えますね。
ラグランジュの補間公式 – Python Code –
# ラグランジュの補間係数関数
def Lagrange_InterpolationFactor(x_list, i, x):
x_i = x_list[i]
res = 1
for cnt, x_atom in enumerate(x_list):
if cnt != i:
res *= (x-x_atom)/(x_i - x_atom)
return res
# ラグランジュの補間公式
def Lagrange_InterpolationFormula(x_list, y_list, x):
res = 0
for n in range(len(x_list)):
res += Lagrange_InterpolationFactor(x_list, n, x) * y_list[n]
return res


コメント