連立一次方程式を解く場合、\(Ax=b\)の\(A\)行列が正方形(行数=列数)でないと\(x\)を逆行列の形で計算できません。しかし複数のデータから解を求める場合や少ないデータから解を求める必要がある場合、必ずしも\(A\)行列が正方形にならないので、この時に一般逆行列を使って解を計算します。この一般逆行列を計算することはどんなことに相当しているのか、図を描いて理解を深めてみましょう。
一般逆行列とは
疑似逆行列、またはムーア・ペンローズの逆行列とも呼ばれるもので、\(Ax=b\)の\(A\)が正方でない場合に解の計算に用いられるものです。\(A\)が縦長の場合( 行数 > 列数 )と、横長の場合 (行数 < 列数 )で計算方法が変わります。
縦長の場合 (行数 > 列数)
\(A\)行列が縦長の場合とは(1)式のような形をしている連立一次方程式です。
$$
\left(\begin{array}{ccc}
a_{11} & a_{12} & a_{13} \\
a_{21} & a_{22} & a_{23} \\
a_{31} & a_{32} & a_{33} \\
a_{41} & a_{42} & a_{43} \\
a_{51} & a_{52} & a_{53}
\end{array}\right)
\left(\begin{array}{c}
x_1 \\ x_2 \\ x_3
\end{array}\right)=
\left(\begin{array}{c}
b_1 \\ b_2 \\ b_3 \\ b_4 \\ b_5
\end{array}\right) \tag{1}
$$
縦長の場合、変数\(\boldsymbol{x} = (x_1, x_2, x_3)^T\)に比べて方程式の数が多いので、解を一つに決めることが出来ません(一意ではない)。
そこで\(A^T\)を左掛けて(2)のように計算すると
$$
\boldsymbol{A}^T \boldsymbol{A} \boldsymbol{x} = \boldsymbol{A}^T \boldsymbol{b} \tag{2}$$
左辺の\(\boldsymbol{A}^T \boldsymbol{A}\)は
$$
\boldsymbol{A}^T \boldsymbol{A} =
\left(\begin{array}{ccccc}
a_{11} & a_{21} & a_{31} & a_{41} & a_{51} \\
a_{12} & a_{22} & a_{32} & a_{42} & a_{52} \\
a_{13} & a_{23} & a_{33} & a_{43} & a_{53}
\end{array}\right)
\left(\begin{array}{ccc}
a_{11} & a_{12} & a_{13} \\
a_{21} & a_{22} & a_{23} \\
a_{31} & a_{32} & a_{33} \\
a_{41} & a_{42} & a_{43} \\
a_{51} & a_{52} & a_{53}
\end{array}\right) =
\left(\begin{array}{ccc}
aa_{11} & aa_{12} & aa_{13} \\
aa_{21} & aa_{22} & aa_{23} \\
aa_{31} & aa_{32} & aa_{33} \\
\end{array}\right)
$$
右辺の\(\boldsymbol{A}^T \boldsymbol{b}\)は
$$
\boldsymbol{A}^T \boldsymbol{b} =
\left(\begin{array}{ccccc}
a_{11} & a_{21} & a_{31} & a_{41} & a_{51} \\
a_{12} & a_{22} & a_{32} & a_{42} & a_{52} \\
a_{13} & a_{23} & a_{33} & a_{43} & a_{53}
\end{array}\right)
\left(\begin{array}{c}
b_1 \\ b_2 \\ b_3
\end{array}\right) =
\left(\begin{array}{c}
ab_1 \\ ab_2 \\ ab_3
\end{array}\right)
$$
となるので、(3)式のように正方形となるので解を計算することが出来ます。
$$
\left(\begin{array}{ccc}
aa_{11} & aa_{12} & aa_{13} \\
aa_{21} & aa_{22} & aa_{23} \\
aa_{31} & aa_{32} & aa_{33} \\
\end{array}\right)
\left(\begin{array}{c}
x_1 \\ x_2 \\ x_3
\end{array}\right) =
\left(\begin{array}{c}
ab_1 \\ ab_2 \\ ab_3
\end{array}\right) \tag{3}
$$
これは多かった方式の数を縮小させて計算する形です。
横長の場合 (行数 < 列数)
\(A\)行列が横長の場合とは(4)式のような形をしている連立一次方程式です。
$$
\left(\begin{array}{ccccc}
a_{11} & a_{21} & a_{31} & a_{41} & a_{51} \\
a_{12} & a_{22} & a_{32} & a_{42} & a_{52} \\
a_{13} & a_{23} & a_{33} & a_{43} & a_{53}
\end{array}\right)
\left(\begin{array}{c}
x_1 \\ x_2 \\ x_3 \\ x_4 \\ x_5
\end{array}\right)=
\left(\begin{array}{c}
b_1 \\ b_2 \\ b_3
\end{array}\right) \tag{4}
$$
横長の場合、変数\(\boldsymbol{x} = (x_1, x_2, x_3, x_4, x_5)^T\)に比べて方程式の数が少ないので、解を一つに決めることが出来ません。
この場合、(5)式のようにして解を計算します。
$$
\boldsymbol{x} = \boldsymbol{A}^T \bigl(\boldsymbol{A} \boldsymbol{A}^T\bigr)^{-1} \boldsymbol{b} \tag{5}
$$
まず\( \boldsymbol{A} \boldsymbol{A}^{T} \)は
$$
\boldsymbol{A} \boldsymbol{A}^{T} =
\left(\begin{array}{ccccc}
a_{11} & a_{21} & a_{31} & a_{41} & a_{51} \\
a_{12} & a_{22} & a_{32} & a_{42} & a_{52} \\
a_{13} & a_{23} & a_{33} & a_{43} & a_{53}
\end{array}\right)
\left(\begin{array}{ccc}
a_{11} & a_{12} & a_{13} \\
a_{21} & a_{22} & a_{23} \\
a_{31} & a_{32} & a_{33} \\
a_{41} & a_{42} & a_{43} \\
a_{51} & a_{52} & a_{53}
\end{array}\right)
=
\left(\begin{array}{ccc}
aa_{11} & aa_{12} & aa_{13} \\
aa_{21} & aa_{22} & aa_{23} \\
aa_{31} & aa_{32} & aa_{33}
\end{array}\right)
$$
\(\boldsymbol{A} \boldsymbol{A}^T\) は3行3列の正方行列なので
$$
\bigl(\boldsymbol{A} \boldsymbol{A}^{T}\bigr)^{-1} =
\left(\begin{array}{ccc}
iaa_{11} & iaa_{12} & iaa_{13} \\
iaa_{21} & iaa_{22} & iaa_{23} \\
iaa_{31} & iaa_{32} & iaa_{33}
\end{array}\right)
$$
と考えます。次に
$$
\boldsymbol{A}^T\bigl(\boldsymbol{A} \boldsymbol{A}^{T}\bigr)^{-1} =
\left(\begin{array}{ccc}
a_{11} & a_{12} & a_{13} \\
a_{21} & a_{22} & a_{23} \\
a_{31} & a_{32} & a_{33} \\
a_{41} & a_{42} & a_{43} \\
a_{51} & a_{52} & a_{53}
\end{array}\right)
\left(\begin{array}{ccc}
iaa_{11} & iaa_{12} & iaa_{13} \\
iaa_{21} & iaa_{22} & iaa_{23} \\
iaa_{31} & iaa_{32} & iaa_{33}
\end{array}\right) =
\left(\begin{array}{ccc}
aiaa_{11} & aiaa_{12} & aiaa_{13} \\
aiaa_{21} & aiaa_{22} & aiaa_{23} \\
aiaa_{31} & aiaa_{32} & aiaa_{33} \\
aiaa_{41} & aiaa_{42} & aiaa_{43} \\
aiaa_{51} & aiaa_{52} & aiaa_{53}
\end{array}\right)
$$
と計算できるので、
$$
\boldsymbol{A}^T\bigl(\boldsymbol{A} \boldsymbol{A}^{T}\bigr)^{-1} \boldsymbol{b}=
\left(\begin{array}{ccc}
aiaa_{11} & aiaa_{12} & aiaa_{13} \\
aiaa_{21} & aiaa_{22} & aiaa_{23} \\
aiaa_{31} & aiaa_{32} & aiaa_{33} \\
aiaa_{41} & aiaa_{42} & aiaa_{43} \\
aiaa_{51} & aiaa_{52} & aiaa_{53}
\end{array}\right)
\left(\begin{array}{c}
b_1 \\ b_2 \\ b_3 \\ b_4 \\ b_5
\end{array}\right) =
\left(\begin{array}{c}
ab_1 \\ ab_2 \\ ab_3 \\ ab_4 \\ ab_5
\end{array}\right)
$$
となるので、(6)式のように解が計算できます。
$$
\left(\begin{array}{c}
x_1 \\ x_2 \\ x_3 \\ x_4 \\ x_5
\end{array}\right) =
\left(\begin{array}{c}
ab_1 \\ ab_2 \\ ab_3 \\ ab_4 \\ ab_5
\end{array}\right) \tag{6}
$$
一般逆行列の計算とその意味
まず正方の形の意味を考える
以下のような連立一次方程式を解いて得られえる解は、両方の式を満たす共通の\((x,y)\)となります。
$$
a_{11} x + a_{12} y = b_1 \\
a_{21} x + a_{22} y = b_2
$$
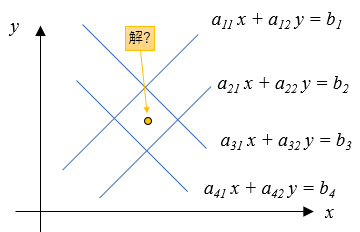
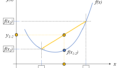
この方程式の解は以下の図のように、直線の交点になります。
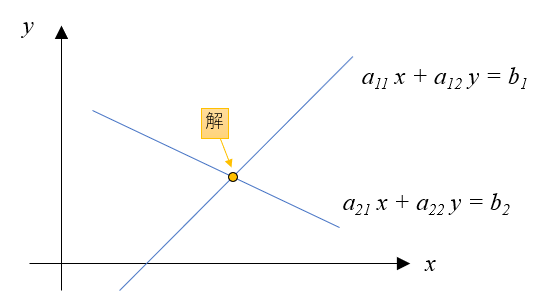
実際にプログラムで計算しても、解の赤点は以下の図のように直線の交点になります。
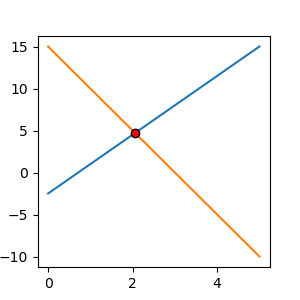
import matplotlib.pylab as plt import numpy as np %matplotlib nbagg import scipy.linalg as linalg # 方程式のパラメータ eq1_param = [-7,2,-5] eq2_param = [5,1, 15] # 方程式 y1 = lambda x1 : (eq1_param[2] - eq1_param[0] *x1 ) / eq1_param[1] y2 = lambda x2 : (eq2_param[2] - eq2_param[0] *x2 ) / eq2_param[1] # 方程式の図示 x_lim = np.linspace(0, 5, 10) y1_lim = y1(x_lim) y2_lim = y2(x_lim) fig = plt.subplots(figsize=(3,3)) plt.plot(x_lim, y1_lim, zorder=1) plt.plot(x_lim, y2_lim, zorder=1) # LU分解で解の計算 A = np.array([eq1_param[:2], eq2_param[:2]]) B = np.array([eq1_param[2], eq2_param[2]]) LU = linalg.lu_factor(A) x = linalg.lu_solve(LU, B) # 図へプロット plt.scatter(x[0], x[1], zorder=2, color='red', edgecolors='black') plt.show()
Aが縦長の場合の意味
(7)式のような縦長の\(A\)の場合で考えます。図で考え易いように2次元で検討します。
$$
\begin{array}{c}
a_{11} x + a_{12} y = b_1 \\
a_{21} x + a_{22} y = b_2 \\
a_{31} x + a_{32} y = b_3
\end{array}
\Rightarrow
\left(\begin{array}{cc}
a_{11} & a_{12} \\
a_{21} & a_{22} \\
a_{31} & a_{32}
\end{array}\right)
\left(\begin{array}{c}
x \\ y
\end{array}\right) =
\left(\begin{array}{c}
b_1 \\ b_2 \\ b_3
\end{array}\right) \tag{7}
$$
これは以下の図のように、すべての直線が一点で交差しないということを意味しています。
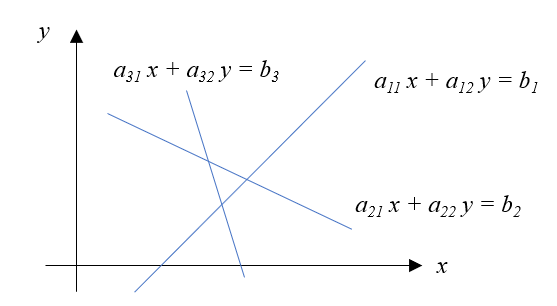
これを \(\boldsymbol{A}^T \boldsymbol{A} \boldsymbol{x} = \boldsymbol{A}^T \boldsymbol{b} \)を使って計算してみます。解はどこに現れるでしょうか?線で構成される三角形の重心?それとも中心でしょうか?
python コード – 縦長の場合 その1
import matplotlib.pylab as plt import numpy as np %matplotlib nbagg import scipy.linalg as linalg # 方程式のパラメータ eq1_param = [-5,1,-10] eq2_param = [5,1, 15] eq3_param = [20, 1, 30] # 方程式 y1 = lambda x1 : (eq1_param[2] - eq1_param[0] *x1 ) / eq1_param[1] y2 = lambda x2 : (eq2_param[2] - eq2_param[0] *x2 ) / eq2_param[1] y3 = lambda x3 : (eq3_param[2] - eq3_param[0] *x3 ) / eq3_param[1] # 方程式の図示 x_lim = np.linspace(0, 5, 10) y1_lim = y1(x_lim) y2_lim = y2(x_lim) y3_lim = y3(x_lim) fig = plt.subplots(figsize=(3,3)) plt.plot(x_lim, y1_lim, zorder=1) plt.plot(x_lim, y2_lim, zorder=1) plt.plot(x_lim, y3_lim, zorder=1) plt.ylim(-20,20) # LU分解を使って解の計算 A = np.array([eq1_param[:2], eq2_param[:2], eq3_param[:2]]) B = np.array([eq1_param[2], eq2_param[2], eq3_param[2]]) At = A.transpose() # 左辺行列の計算 AtA = np.dot(At, A) # 右辺行列の計算 AtB = np.dot(At, B) # 解の計算 LU = linalg.lu_factor(AtA) x = linalg.lu_solve(LU, AtB) # 解の位置を図示 plt.scatter(x[0], x[1], zorder=2, color='red', edgecolors='black') plt.show()
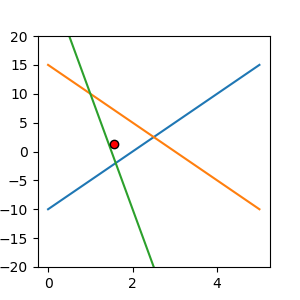
赤点が解の位置です。各交点の重心または中心が解になると思っていましたが、そうではなく緑の線に近いところに解が現れていますね。
一般逆行列を解くための評価関数
縦長のAを一般逆行列で解くことは、以下の評価関数\(J\)を最小にすること意味しています。
$$
J = \frac{1}{2} \sum_{k=1}^{m} \bigl( a_{k1} x_1 + a_{k2} x_2 + \cdots + a_{kn} x_n – b_n \bigl) ^2
$$
今回の場合では\(J\)は以下のようになります。
$$
J = \frac{1}{2} \Bigl( \bigl(a_{11} x + a_{12} y – b_1 \bigr)^2 + \bigl(a_{21} x + a_{22} y – b_2 \bigr)^2 + \bigl(a_{31} x + a_{32} y – b_3 \bigr)^2 \Bigl)
$$
この評価関数\(J\)を最小化することを考えてみます。
最小であるとは\(J=0\)であるので、それぞれの項\(( a_{k1} x + a_{k2} y – b_k , k=1,2,3)\)がゼロになっていればいいですね。それぞれの項がゼロになるとは、例えば、
$$
a_{11} x + a_{12} y – b_1 = 0
$$
ということですが、これは以下のように線分上の\((x,y)\)があるということを意味しています。
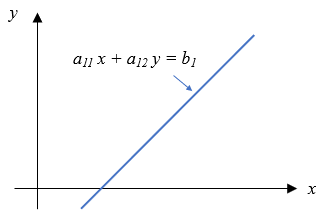
複数の線分(方程式)が一点で交差しない場合、\((x,y)\)が線分上に乗らないので \(a_{k1} x + y – b_k = \delta_k\) という感じで右辺が\(0\)ではなくなります。
\(y\)の係数\(a_{k2}\)を\(1\)と考えると、 \((x,y)\)が\(a_{k1} x + y – b_k =0\)の線分から離れるということは、以下の図のように\(a_{k1}\)が大きければ\(x\)のずれ\(\Delta x\)が\(a_{k1} x + y – b_k = \delta_k\)の誤差:\(\delta_k\)へ影響することになります。
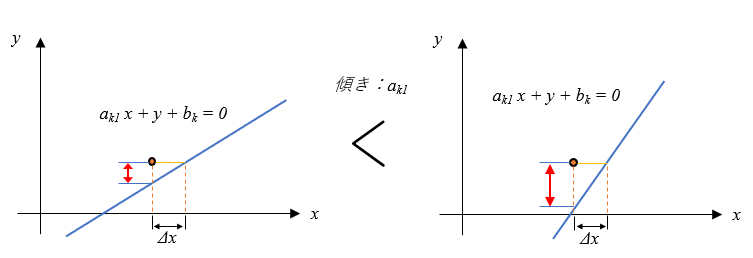
つまり、以下の\(J\)の最小化を考える場合、傾きがより大きな方程式へ解を寄せることが\(J\)の最小化へとつながっています。
任意の位置へ解を持ってくる
傾きが大きい方程式へ解が寄るということは、以下のように方程式のすべての傾きが同じであれば、中心の位置が解になるはずです。
プログラムで検証してみると、
python コード : 縦長の場合 – その2
import matplotlib.pylab as plt
import numpy as np
%matplotlib nbagg
import scipy.linalg as linalg
# 方程式のパラメータ
eq1_param = [-1,1,0]
eq2_param = [1,1, 20]
eq3_param = [-1, 1, -10]
eq4_param = [1, 1, 30]
# 方程式
y1 = lambda x1 : (eq1_param[2] - eq1_param[0] *x1 ) / eq1_param[1]
y2 = lambda x2 : (eq2_param[2] - eq2_param[0] *x2 ) / eq2_param[1]
y3 = lambda x3 : (eq3_param[2] - eq3_param[0] *x3 ) / eq3_param[1]
y4 = lambda x4 : (eq4_param[2] - eq4_param[0] *x4 ) / eq4_param[1]
# 方程式を図示
x_lim = np.linspace(0, 30, 10)
y1_lim = y1(x_lim)
y2_lim = y2(x_lim)
y3_lim = y3(x_lim)
y4_lim = y4(x_lim)
fig,ax = plt.subplots(figsize=(3,3))
plt.plot(x_lim, y1_lim, zorder=1)
plt.plot(x_lim, y2_lim, zorder=1)
plt.plot(x_lim, y3_lim, zorder=1)
plt.plot(x_lim, y4_lim, zorder=1)
plt.xlim(5,25)
plt.ylim(0,20)
# LU 分解で解の計算
A = np.array([eq1_param[:2], eq2_param[:2], eq3_param[:2], eq4_param[:2]])
B = np.array([eq1_param[2], eq2_param[2], eq3_param[2], eq4_param[2]])
# 一般逆行列の作成
At = A.transpose()
AtA = np.dot(At, A)
AtB = np.dot(At, B)
# LU分解で解を計算
LU = linalg.lu_factor(AtA)
x = linalg.lu_solve(LU, AtB)
# 解の位置を図示
plt.scatter(x[0], x[1], zorder=2, color='red', edgecolors='black')
ax.set_aspect('equal')
ax.grid(True)
plt.show()
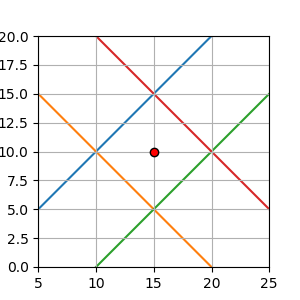
一般逆行列の解:赤点がそれぞの線分の交点の中心に設定できました。
Aが横長の場合の意味
Aが横長の場合を(8)式で考えてみます。
$$
\begin{array}{c}
a_{11} x + a_{12} y = b_1
\end{array}
\Rightarrow
\left(\begin{array}{cc}
a_{11} & a_{12}
\end{array}\right)
\left(\begin{array}{c}
x \\ y
\end{array}\right)=
\left(\begin{array}{c}
b_1
\end{array}\right) \tag{8}
$$
求めるべき解は\((x,y)\)の二つですが、方程式が一つなので解が計算できません。図的な意味では、\((x,y)\)は線分上のどこでもよいので、無数に存在することになります。
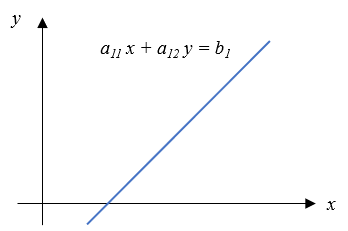
では横長の場合の一般逆行列の計算\((\boldsymbol{x}=\boldsymbol{A}^T\bigl(\boldsymbol{A} \boldsymbol{A}^{T}\bigr)^{-1} \boldsymbol{b})\)を行ってみましょう。
python コード : 横長の場合 – その1
import matplotlib.pylab as plt
import numpy as np
%matplotlib nbagg
import scipy.linalg as linalg
# 方程式のパラメータ
eq1_param = [-1,1,-4]
# 方程式
y1 = lambda x1 : (eq1_param[2] - eq1_param[0] *x1 ) / eq1_param[1]
# 方程式の図示
x_lim = np.linspace(0, 10, 10)
y1_lim = y1(x_lim)
fig,ax = plt.subplots(figsize=(3,3))
plt.plot(x_lim, y1_lim, zorder=1)
plt.ylim(-5,5)
# 一般逆行列で解の計算
A =np.array([eq1_param[:2]])
B = np.array([eq1_param[2]])
At = A.transpose()
AAt = np.dot(A, At)
AAt_inv = np.linalg.inv(AAt)
AtAAt_inv = np.dot(At, AAt_inv)
x = np.dot(AtAAt_inv, B)
# 解を図示
plt.scatter(x[0], x[1], zorder=2, color='red', edgecolors='black')
ax.set_aspect('equal')
plt.show()
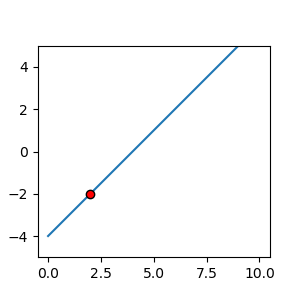
こんな感じで解が一点に決まりました。
一般逆行列を解くための制約条件と評価関数
Aが横長の場合、一般逆行列を計算することは、もともとの連立一次方程式を制約条件として、以下の評価関数\(J\)を最小化することを意味しています。
$$
J = \frac{1}{2} \bigl( x_1 ^2 + x_2 ^2 + \cdots + x_n ^2 \bigr)
$$
今回の(8)式の計算では、
制約条件:\(a_{11} x + a_{12} y = b_1\)
評価関数:\(J = \frac{1}{2} \bigl( x^2 + y^2 \bigr)\)
この\(J\)は\((0,0)\)を原点とした円であると考えることが出来るので、以下の図ように、解は線と\((0,0)\)を原点とした円の接点であるといえます。
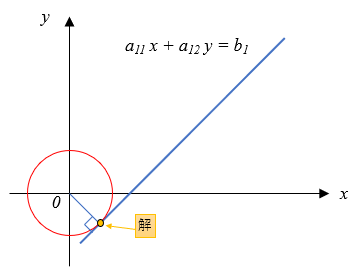
先ほどの解を利用してプログラムで計算で図示すると
import matplotlib.patches as patches
import math
# 図の作成
fig,ax = plt.subplots(figsize=(3,3))
plt.plot(x_lim, y1_lim, zorder=1)
plt.ylim(-5,5)
# 解の図示
plt.scatter(x[0], x[1], zorder=2, color='red', edgecolors='black')
# 中心(0,0)とした円の図示
radius = math.sqrt(x[0]**2 + x[1]**2)
circle = patches.Circle([0,0], radius=radius, fill=False, linestyle='--')
ax.add_patch(circle)
ax.set_aspect('equal')
plt.show()
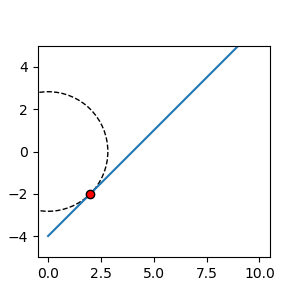
このように中心が\((0,0)\)である円と方程式の解が接円の関係となっていますね。
3次元空間で考える
次はXYZの3次元空間に2本の線がある場合の(9)式で考えみます。
$$
\begin{array}{c}
a_{11} x + a_{12} y + a_{13} z = b_1 \\
a_{21} x + a_{22} y + a_{23} z = b_2
\end{array}
\Rightarrow
\left(\begin{array}{cc}
a_{11} & a_{12} & a_{13} \\
a_{21} & a_{22} & a_{23}
\end{array}\right)
\left(\begin{array}{c}
x \\ y \\ z
\end{array}\right) =
\left(\begin{array}{c}
b_1 \\ b_2
\end{array}\right) \tag{9}
$$
図で描くと以下のような感じです。
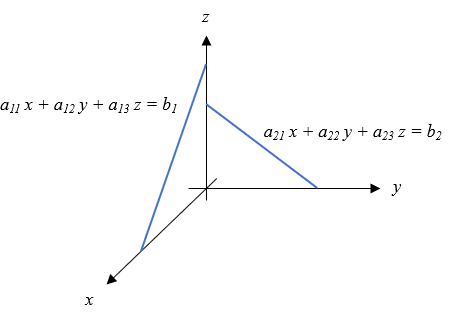
実際には(9)式は平面の一般式ですが\(a_{12} = a_{21}=0\)とすることで、一本の線分はXZ平面にあり、もう一本の線分はYZ平面にあるとします。二つの直線は互いに交わらないねじれの関係があるとする、通常の方法では解が計算できません。
では一般化逆行列で解を計算しましょう。
python コード : 横長の場合 – その2
import matplotlib.pyplot as plt
import numpy as np
from mpl_toolkits.mplot3d import Axes3D
%matplotlib nbagg
import scipy.linalg as linalg
# 方程式のパラメータ
eq1_param = [2 ,0, 1,8]
eq2_param = [0, 1, 1, 4]
# 方程式
z1 = lambda x, y : (eq1_param[3] - eq1_param[0] *x - eq1_param[1] * y ) / eq1_param[2]
z2 = lambda x, y : (eq2_param[3] - eq2_param[0] *x - eq2_param[1] * y ) / eq2_param[2]
x_lim = np.linspace(0, 10, 10)
y_lim = np.linspace(0, 10, 10)
z1_lim = z1(x_lim, y_lim)
z2_lim = z2(x_lim, y_lim)
# 一般逆行列で解の計算
A =np.array([eq1_param[:3], eq2_param[:3]])
B = np.array([eq1_param[3], eq2_param[3]])
At = A.transpose()
AAt = np.dot(A, At)
AAt_inv = np.linalg.inv(AAt)
AtAAt_inv = np.dot(At, AAt_inv)
x = np.dot(AtAAt_inv, B)
# 方程式の図示
fig = plt.figure(figsize=(4,4))
ax1 = fig.add_subplot(111, projection='3d')
ax1.plot(x_lim, np.linspace(0,0,10), z1_lim, zorder=1)
ax1.plot(np.linspace(0,0,10), y_lim, z2_lim, zorder=1)
# 解の図示
ax1.scatter(x[0], x[1], x[2], zorder=2, color='red', edgecolors='black')
ax1.set_xlabel('x')
ax1.set_ylabel('y')
ax1.set_zlabel('z')
plt.show()
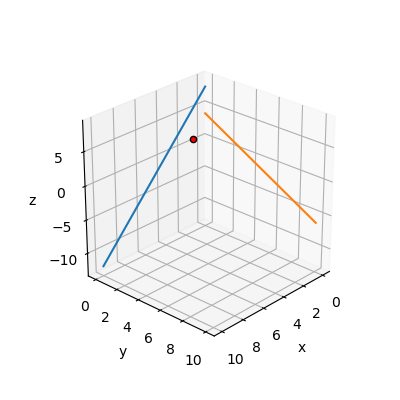
こんな感じで\((x,y,z)\)の位置へ解が現れました。XY平面とYZ平面でこの解を見ると以下の図のように線上(方程式上)にあることが分かります。
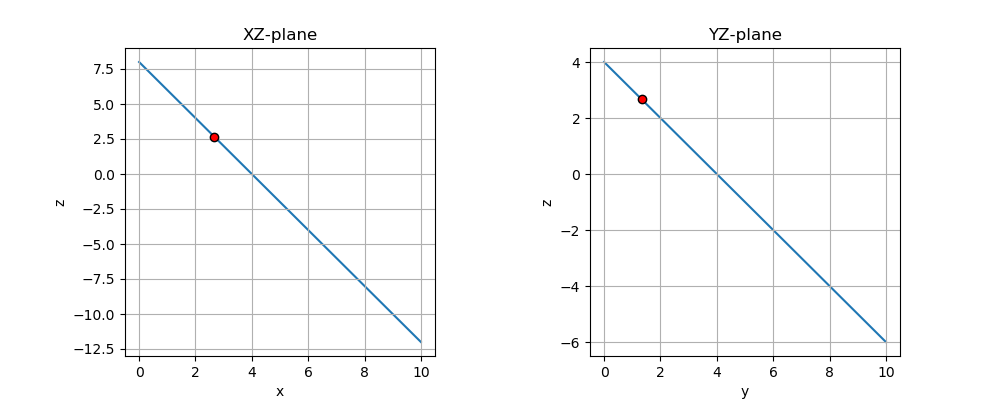
これにより、今回の制約条件である(9)式を満たしていることが分かります。
$$
\begin{array}{c}
a_{11} x + a_{12} y + a_{13} z = b_1 \\
a_{21} x + a_{22} y + a_{23} z = b_2
\end{array} \tag{9}
$$
中心を\((0,0,0)\)とする半径 \(r = \sqrt{x^2 + y^2 + z^2}\)とする球をそれぞの平面で描いても
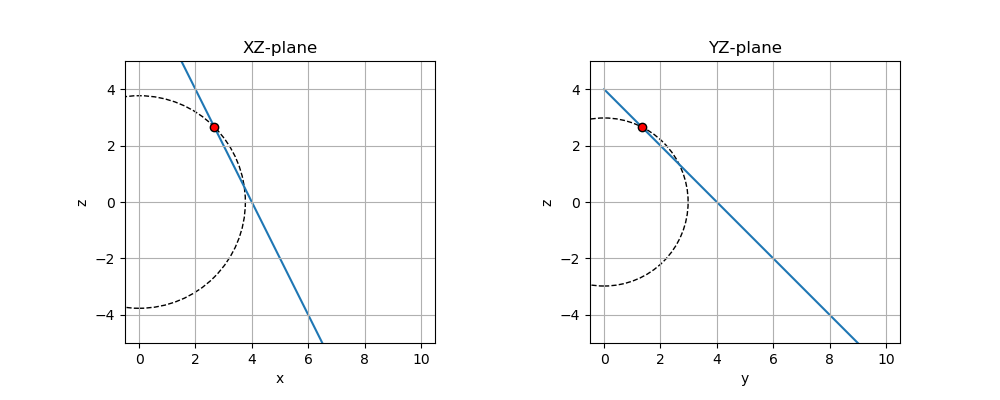
このように点と線が乗っていることが分かります。球なので、ちょっと見辛いですが、\((0,0,0)\)と直線をなす平面で見れば、ちゃんと接円の関係になっていることが見て取れます。
ということでAが横長の場合の一般逆行列の解は、制約条件の方程式上であり、その中で原点に最も近いところが解になることが分かります。
4次元の場合
図示はできませんが、4次元の場合で横長のAを一般逆行列で解を求め、それが制約条件を満たしているか確かめてみます。
$$
\begin{array}{c}
a_{11} x_1 + a_{12} x_2 + a_{13} x_3 + a_{14} x_4 = b_1 \\
a_{21} x_1 + a_{22} x_2 + a_{23} x_3 + a_{24} x_4 = b_2 \\
a_{31} x_1 + a_{32} x_2 + a_{33} x_3 + a_{34} x_4 = b_3 \\
\end{array}
\Rightarrow
\left(\begin{array}{cccc}
a_{11} & a_{12} & a_{13} & a_{14} \\
a_{21} & a_{22} & a_{23} & a_{24} \\
a_{31} & a_{32} & a_{33} & a_{34} \\
\end{array}\right)
\left(\begin{array}{c}
x_1 \\ x_2 \\ x_3 \\ x_4
\end{array}\right) =
\left(\begin{array}{c}
b_1 \\ b_2 \\ b_3
\end{array}\right)
$$
python コード : Aが横長の場合 -その3
import numpy as np import scipy.linalg as linalg # 方程式のパラメータ eq1_param = [2 ,4, 1, 4, 8] eq2_param = [-8, -1, 1, 4, -40] eq3_param = [-1, -4, 2, -6, 1] # 一般逆行列で解の計算 A =np.array([eq1_param[:4], eq2_param[:4], eq3_param[:4]]) B = np.array([eq1_param[4], eq2_param[4], eq3_param[4]]) At = A.transpose() AAt = np.dot(A, At) AAt_inv = np.linalg.inv(AAt) AtAAt_inv = np.dot(At, AAt_inv) x = np.dot(AtAAt_inv, B) # 制約条件を満たしているか計算 eq1_ans = x[0] * eq1_param[0] + x[1] * eq1_param[1] + x[2] * eq1_param[2] + eq1_param[3] * x[3] - eq1_param[4] eq2_ans = x[0] * eq2_param[0] + x[1] * eq2_param[1] + x[2] * eq2_param[2] + eq2_param[3] * x[3] - eq2_param[4] eq3_ans = x[0] * eq3_param[0] + x[1] * eq3_param[1] + x[2] * eq3_param[2] + eq3_param[3] * x[3] - eq3_param[4] # 出力 print(eq1_ans) ### 3.552713678800501e-15 print(eq2_ans) ### 0.0 print(eq3_ans) ### -4.440892098500626e-15
制約条件は元の方程式であるので、\( a_{k1} x_1 + a_{k2} x_2 + a_{k3} x_3 + a_{k4} x_4 – b_k = 0\)を満たしていることが確認できました。

コメント