\(dy/dx = f(x,y)\)の常微分方程式から解析的に\(y(x)\)が解ければ、どんな\(x\)における\(y(x)\)でも計算できますが、なかなかそうはいきません。運動方程式も微分方程式で表されているので、このシステムはどんな振る舞いをするの?という疑問に答えるにはやはり解析解が必要です。でもやっぱり解析解を求めることが難しいので、そんなときに役立つツールの一つが数値計算のオイラー法です。
オイラー法をバネ-マス系の運動方程式に適用してシステムの振る舞いを数値計算して、解析解との比較を行ってみます。
オイラー法とは
変数が一つである微分法手式を常微分方程式と呼びます。変数が\(x\)である常微分方程式 \(dy(x)/dx = f(x,y(x))\)の解が\(y(x)\)であるとします。
このとき、この\(y(x)\)の少し先の点\(x+h\)について表すと、テイラー展開を用いて(1)式で表されます。
$$
y(x+h) = y(x) + h \frac{d y(x) } {dx} + \frac{h^2}{2!} \frac{d^2 y(x)}{dx^2} + \cdots \tag{1}
$$
\(dy(x)/dx = f(x,y(x))\)の関係を(1)式に当てはめると(2)式になります。
$$
y(x+h) = y(x) + h f(x,y(x)) + \frac{h^2}{2!} \frac{d}{dx}f(x,y(x)) + \cdots \tag{2}
$$
(2)式から、(3)式のように\(f(x,y(x))\)の1階微分以上を利用しないで解\(y(x)\)の次の点\(y(x+h)\)を計算することをオイラー法といいます。
$$
y(x+h) = y(x) + h f(x,y(x)) \tag{3}
$$
一階微分以上を無視しているので、数値計算の誤差が大きいことが特徴です。ではこれを運動方程式に適用してみます。
このように\(y(x+h)\)の計算を\(y(x)\)と\(x\)だけで行う方法を一段式といいます。ちなみに \(y(x+h)\)の計算を\(y(x), y(x-h), y(x – 2h), \cdots\)と\(x\)を使い計算する方法は多段式です。
システムの運動方程式
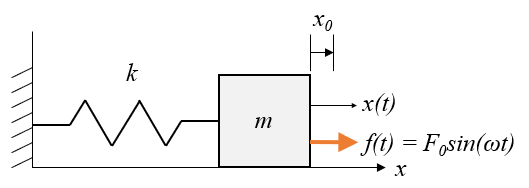
オイラー法で計算する運動方程式は、減衰項が無いバネ-マス系に振動を加えたシステムです。
このシステムの運動方程式はニュートンの運動方程式から(4)式となります。
$$
f(t) = m \frac{d^2 x(t)}{d t^2} + k x(t) \tag{4}
$$
運動方程式にオイラー法を適用
オイラー法は\(dy(x)/dx = f(x,y(x))\)の形の式に適用するので(5)式を定義します。
$$
\frac{d x(t) }{ d t} = v(t) \tag{5}
$$
すると(4)式は(6)式になります。
$$
f(t) = m \frac{d v(t)}{d t} + k x(t) \tag{6}
$$
\(dy(x)/dx = f(x,y(x))\) の形で書くと(7)式のようになります。
$$
\begin{eqnarray}
\frac{d x(t) }{ d t} &=& v(t) \\
\frac{d v(t)}{d t} &=& \frac{1}{m} \big(f(t)-kx(t) \big)
\end{eqnarray} \tag{7}
$$
(3)式のオイラー法を適用すると、(8)式となります。
$$
\begin{eqnarray}
x(t+h) &=& x(t) + h v(t) \\
v(t + h) &=& v(t) + \frac{h}{m} \big(f(t) -kx(t+h) \big)
\end{eqnarray} \tag{8}
$$
オイラー法で計算
パラメータを以下のようにしてPythonで計算させてその運動波形を確認します。外力\(f(t)\)は\(F_0 \sin (\omega )t\)の周期的な力です。
| \(x(0) [m]\) | 0.1 |
| \(v(0) [m/s]\) | 0 |
| \(k [N/m]\) | 5 |
| \(m [kg]\) | 0.1 |
| \(F_0 [N]\) | 2 |
| \(\omega [rad] \) | 12.56 |
import matplotlib.pyplot as plt
from math import sin,pi
# パラメータ
v0 = 0
x0 = 0.1
m = 0.1 # [kg]
k = 5 # [N/m]
F0 = 2 # [N]
f = 2 # [Hz]
omega = 2*pi*f
# 刻み幅
h = 0.02 # [sec]
x_array = [x0]
v_array = [v0]
t_array = [0]
#オイラー法で計算
for i in range(1,500):
t = i * h
x_next = x_array[i-1] + h * v_array[i-1]
v_next = v_array[i-1] + h/m * (F0* sin(omega*t) - k * x_next)
t_array.append(t)
x_array.append(x_next)
v_array.append(v_next)
#図示
plt.figure(figsize=(10,4))
plt.plot(t_array, x_array)
plt.xlabel("time[sec]")
plt.ylabel(r"$x(t)$[m]")
plt.grid(True)
plt.xticks([i for i in range(11)])
plt.show()

それっぽい計算結果になりましたね。ではこの結果を解析解と比べてみましょう。
解析解とオイラー法の比較
バネ-マス系の解析解は(9)式でした。
$$
x(t) = x_0 \cos \omega_0 t + \bigg(\frac{v_0}{\omega_o} – \frac{\omega}{\omega_0}\frac{F_0/m}{\omega_0^2 – \omega^2}\bigg) \sin \omega_0 t + \frac{F_0/m}{\omega_0^2 – \omega^2} \sin \omega t \tag{9}
$$
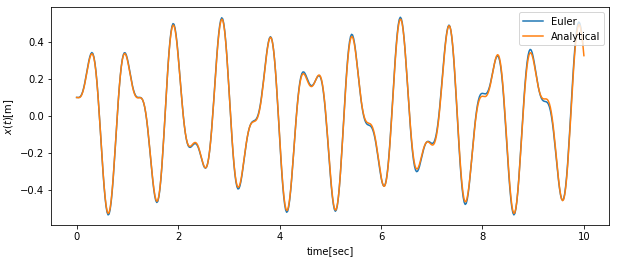
この式で計算した値とオイラー法の計算結果を一緒に描くと以下の図のように、ほとんど一致しています。青線がオイラー法、オレンジ線が解析解です。
計算誤差について
解析解とオイラー法の誤差(解析解 – オイラー法)は以下のように、だんだんと誤差が広がっていくようになっています。

\(t=0\)から3ステップまでの微小区間で解析解とオイラー法を描くと以下のようになります。
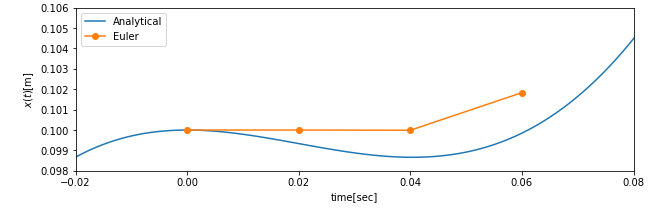
オイラー法の計算が始まる \(t=0\)では解析解との差は生じていません。オイラー法は次の点を、この\(t=0\)時点における勾配を使って計算するので、このように誤差が生じます。またその次の点も勾配を使うのでさらにずれていきます。
オイラー法はこのように誤差が大きいことが特徴ですが、システムの振る舞いを確認するだけならこの方法でもいいのかなと思います。

コメント