質点とバネが付いたシステムの解析解を計算します。外力が無い場合の自由振動解と、外力を与える場合の強制振動解の二つを求めます。それから、Pythonで計算して応答波形を確認してみましょう。
運動方程式
外力が無い場合
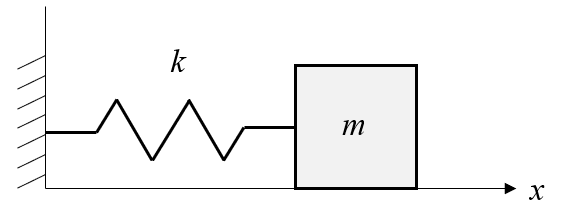
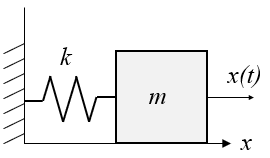
\(k\)はバネ定数[N/m]、\(m\)は質点[kg]です。質点\(m\)は床から離れずに左右に運動し、その位置を\(x(t)\)とします。このシステムの運動方程式はニュートンの運動方程式より(1)式になります。
$$
m\frac{d^2 x(t)}{d t^2} + k x(t) = 0 \tag{1}
$$
外力を受ける場合
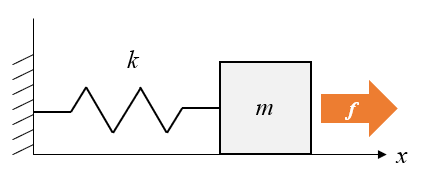
外力\(f[N]\)は質点に加わります。これも同じくニュートンの運動方程式より(2)式になります。
$$
m\frac{d^2 x(t)}{d t^2} + k x(t) = f(t) \tag{2}
$$
運動方程式の解析解
外力が無い場合 – 自由振動解
(1)式の運動方程式の解を求めていきます。外力を受けない場合、自分自身の質量によって揺れるので、自由振動と呼ばれています。
\(k/m = \omega_0^2\)とすると、(1)式は(3)式になります。ちなみにこの\(\omega_0\)は固有振動です。
$$
\frac{d^2 x(t)}{d t^2} + \omega_0^2 x(t) = 0 \tag{3}
$$
(3)式の微分方程式の解を(4)式とします。
$$
x(t) = A \cos \omega_0 t+ B \sin \omega_0 t \tag{4}
$$
(4)式が(3)式を満たしているか確認するため、(3)式に代入して右辺がゼロとなることを確認します。
まず、2階微分を行うと、
$$
\begin{eqnarray}
\frac{d x(t)}{dt} &=& -A \omega_0 \sin \omega_0 t + B \omega_0 \cos \omega_0 t \\
\frac{d^2 x(t)}{dt^2} &=& – A \omega_0^2 \cos \omega_0 t – B \omega_0^2 \sin \omega_0 t
\end{eqnarray}
$$
この2階微分と(4)式を(3)式に代入します。
$$
-A \omega_0^2 \cos \omega_0 t -B \omega_0^2 \sin \omega_0 t + A \omega_0^2 \cos \omega_0 t + B \omega_0^2 \sin \omega_0 t = 0
$$
となるので、(4)式が(3)式の解であることが確認できました。
(4)式の\(A,B\)は初期条件により決まる値です。そこで、\(t=0\)の時、\(x(0) = x_0, dx(0)/dt = v_0\)とします。すると、
$$
x_0 = A \cos( \omega_0 \cdot 0 )+ B \sin (\omega_0 \cdot 0) = A \\
v_0 = -A \omega_0 \sin (\omega_0 \cdot 0 )+ B \omega_0 \cos( \omega_0 \cdot 0) = B \omega_0
$$
となるので、\(A,B\)は(5)式になります。
$$
\begin{eqnarray}
A &=& x_0 \\
B &=& v_0 / \omega_0
\end{eqnarray} \tag{5}
$$
自由振動解
初期条件を \(t=0: x(t) = x_0, dx/dt = v_0\)とした場合、自由振動解は(6)式です。
$$
x(t) = x_0 \cos \omega_0 t+ \frac{v_0}{\omega_0} \sin \omega_0 t \tag{6}
$$
外力を受ける場合 – 強制振動解
強制振動解は、さっき求めた自由振動解の(4)式に、(2)式の運動方程式の解を加えたものです。微分方程式は一般解と特殊解というものがあり、(1)式のように右辺がゼロの微分方程式の解を一般解、(2)式のように右辺がゼロでなく何か値を与えた場合の解を特殊解といいます。強制振動解はこの一般解と特殊解を合わせた形で表されます。
では(2)式の運動方程式の解を求めていきます。
$$
m\frac{d^2 x(t)}{dt^2} + k x(t) = f(t) \tag{2}
$$
まず、加える力を周期的なものとして\(f(t) = F_0 \sin \omega t\)とします。ここで\(F_0\)は加える力の振幅[N]、\(\omega\)は周期[rad]です。
そうすると、\(k/m = \omega_0^2\)として、(2)式は(7)式になります。
$$
\frac{d^2 x(t)}{dt^2} + \omega_0^2 x(t) = \frac{F_0}{m} \sin \omega t \tag{7}
$$
周期的な加振力\(f(t)\)により、(7)式の解である変位 \(x(t)\)は、はやり周期的な変化すると考えて(8)式とします。
$$
x(t) = C \sin \omega t \tag{8}
$$
(8)式を(7)式に代入して係数\(C\)を求めます。まずは微分です。
$$
\begin{eqnarray}
\frac{dx(t)}{dt} &=& C \omega \cos \omega t \\
\frac{d^2x(t)}{dt^2} &=& -C \omega^2 \sin \omega t
\end{eqnarray}
$$
この結果と(8)式を(7)式へ代入し\(C\)を求めます。
$$
-\omega^2 C \sin \omega t + C \omega_0^2 \sin \omega t = F_0/m \sin \omega t \\
-\omega^2 C + C \omega_0^2 = F_0/m \\
C(\omega_0^2 – \omega^2) = F_0/m \\
C = \frac{F_0/m}{\omega_0^2 – \omega^2}
$$
ということで(2)式の運動方程式の解は(9)式になります。この(9)式が(2)式を満たしているとはさっきのCを求める過程で分かります。というより、(2)式を満たすように\(C\)を決めたというほうが正解ですね。
$$
x(t) = \frac{F_0/m}{\omega_0^2 – \omega^2} \sin \omega t \tag{9}
$$
この(10)式は、加えた周期的な加振力と、システムが持っている固有振動数\(\omega_0\)との関連により生じる変位なので、定常振動と呼ばれます。
強制振動解は(9)式と(4)式を加えた形になるので、(10)式です。
$$
x(t) = A \cos \omega_0 t + B \sin \omega_0 t + \frac{F_0/m}{\omega_0^2 – \omega^2} \sin \omega t \tag{10}
$$
AとBは初期条件により決定します。このAとBは自由振動と強制振動で異なるため、自由振動で求めたA、Bは使用できません。新たに(11)式から求める必要があります。
初期条件を\(t = 0 : x(0) = x_0, dx(0)/dt =v_0\)とします。
まずAの計算です。
$$
x_0 = A \cos (\omega_0 \cdot 0) + B \sin (\omega_0 \cdot 0) +\frac{F_0/m}{\omega_0^2 – \omega^2} \sin( \omega \cdot 0) = A\
$$
ここから \(A=x_0\)です。次にBの計算です。
$$
\begin{eqnarray}
v_0 &=& -A \omega_0 \sin( \omega_0 \cdot 0) + \omega_0 B \cos (\omega_0 \cdot 0) + \omega \frac{F_0/m}{\omega_0^2 – \omega^2} \cos( \omega \cdot 0) \\
v_0 &=& \omega_0 B + \omega \frac{F_0/m}{\omega_0^2 – \omega^2} \\
\omega_0 B &=& v_0 – \omega \frac{F_0/m}{\omega_0^2 – \omega^2} \\
B &=& \frac{v_0}{\omega_o} – \frac{\omega}{\omega_0}\frac{F_0/m}{\omega_0^2 – \omega^2}
\end{eqnarray}
$$
強制振動解
初期条件 \(t = 0 : x(0) = x_0, dx(0)/dt =v_0\) としたときの強制振動の解は(11)式になります。
$$
x(t) = x_0 \cos \omega_0 t + \bigg(\frac{v_0}{\omega_o} – \frac{\omega}{\omega_0}\frac{F_0/m}{\omega_0^2 – \omega^2}\bigg) \sin \omega_0 t + \frac{F_0/m}{\omega_0^2 – \omega^2} \sin \omega t \tag{11}
$$
それでは計算できた自由振動解と強制振動解の波形をPythonを使って描いてみます。
波形計算
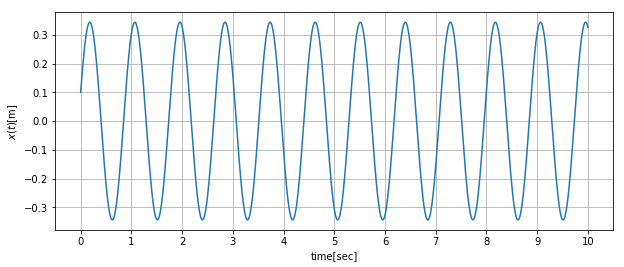
自由振動波形
自由振動解は以下の式です。
$$
x(t) = x_0 \cos \omega_0 t+ \frac{v_0}{\omega_0} \sin \omega_0 t
$$
初期条件 \(x(0) = x_0, v(0) = v_0\)として\(x(t)\)の計算を行います。パラメータは次の値です。
| \(x_0 [m]\) | 0.1 |
| \(v_0 [m/s]\) | 0 |
| \(k [N/m]\) | 5 |
| \(m [kg]\) | 0.1 |
import numpy as np
import matplotlib.pyplot as plt
# パラメータ
x0 = 0.1 #[m]
v0 = 0 # [m/s]
k = 5 #[N/m]
m = 0.1 #[kg]
omega0 = sqrt(k/m)
# 自由振動解
x = lambda t : x0 * np.cos(omega0 * t) + v0/omega0 *np.sin(omega0 * t)
# 時間設定
t_array = np.linspace(0,10,1000)
# xの波形
x_array = x(t_array)
# 図示
plt.figure(figsize=(10,4))
plt.plot(t_array, x_array)
plt.xlabel("time[sec]")
plt.ylabel(r"$x(t)$[m]")
plt.grid(True)
plt.xticks([i for i in range(11)])
plt.show()
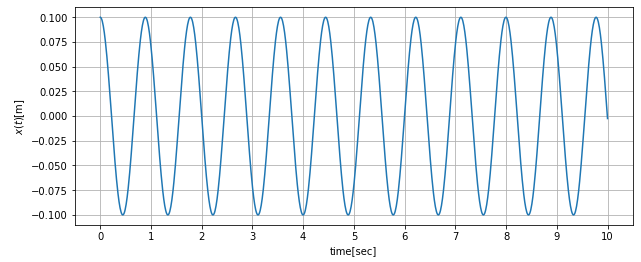
綺麗に計算できました。減衰項が無いので時間がたっても初期条件の\(x_0\)から振幅が減っていませんね。
固有振動\(\omega_0\)は7.071[rad]\(\simeq\)1.125[Hz]なので、この周期で振動していることが分かります。
強制振動波形
強制振動解は以下の式です。
$$
x(t) = x_0 \cos \omega_0 t + \bigg(\frac{v_0}{\omega_o} – \frac{\omega}{\omega_0}\frac{F_0/m}{\omega_0^2 – \omega^2}\bigg) \sin \omega_0 t + \frac{F_0/m}{\omega_0^2 – \omega^2} \sin \omega t
$$
初期条件 \(x(0) = x_0, v(0) = v_0\)として\(x(t)\)の計算を行います。強制振動\(f(t)\)は周期的な力\(F_0 \sin(\omega t)\)を加えます。パラメータは次の値です。
| \(x_0 [m]\) | 0.1 |
| \(v_0 [m/s]\) | 0 |
| \(k [N/m]\) | 5 |
| \(m [kg]\) | 0.1 |
| \(F_0 [N]\) | 2 |
| \(\omega [rad] \) | 12.56 |
import matplotlib.pyplot as plt
import numpy as np
# パラメータ
x0 = 0.1 #[m]
v0 = 0 # [m/s]
m = 0.1 # [kg]
k = 5 # [N/m]
F0 = 2 # [N]
f = 2 # [Hz]
omega0 = np.sqrt(k/m)
omega = 2*np.pi*f
# 強制振動解
B = (v0/omega0 - (omega * F0)/(m*omega0*(omega0**2 - omega**2)))
C = F0/m/(omega0**2 - omega**2)
x = lambda t : x0 * np.cos(omega0 * t) + B * np.sin(omega0 * t ) + C * np.sin(omega * t)
# 時間設定
t_array = np.linspace(0,10,1000)
# xの応答波形
x_array = x(t_array)
# 図示
plt.figure(figsize=(10,4))
plt.plot(tana_array, xana_array)
plt.xlabel("time[sec]")
plt.ylabel(r"$x(t)$[m]")
plt.grid(True)
plt.xticks([i for i in range(11)])
plt.show()
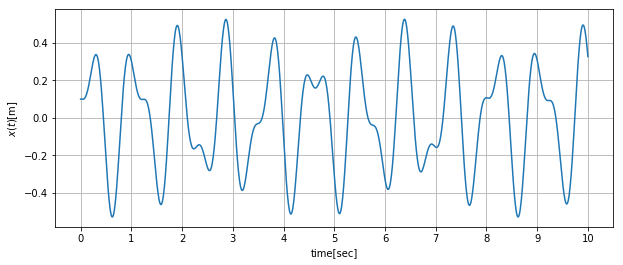
強制振動の波形は、自由振動と加えている周期的な力による定常振動が重畳する形で現れるので、分解して表示してみます。
自由振動波形
定常振動波形
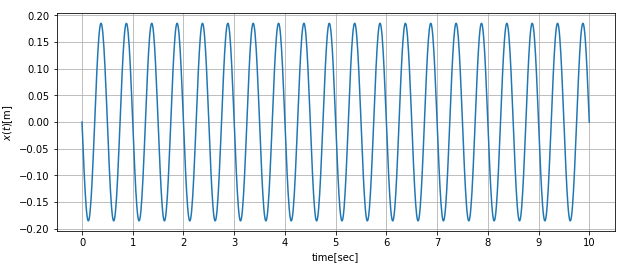
確かに自由振動波形と定常振動波形が加われば、強制振動の波形になりますね。

コメント