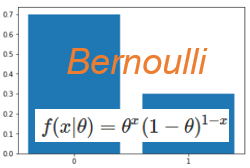
コインを投げて表が出るか裏が出るかや、扉を開けたら人が居るか居ないかなど、2値の結果になる分布をベルヌーイ分布で表すことが出来ます。
確率分布、期待値、分散
確率分布
ベルヌーイ分布に従う確率変数は(1)式の確率分布に従います。\(\theta\)が母数で\(x\)が結果です。
$$
f(x | \theta) = \theta ^ x ( 1- \theta)^{1-x}, \quad x = 0 , 1 \tag{1}
$$
例えば\(\theta\) : コインを投げて表が出る確率<br>
\(x\) : コインを投げた結果 (1を表、0を裏とします)
\(\theta = 0.3\)とすると、
$$
\begin{eqnarray}
f(x = 1 | \theta = 0.3) &=& 0.3^1 ( 1 – 0.3)^{1-1} = 0.3 \\
f(x = 0 | \theta = 0.3) &=& 0.3^0 ( 1 – 0.3)^{1-0} = 0.7 \\
\end{eqnarray}
$$
表(1)が出る確率 0.3、裏(0)が出る確率 0.7と計算できます。
期待値と分散
ベルヌーイ分布に従う確率変数\(X\)の期待値\(E[X]\)は、分散\(V[X]\)は次の式です。
$$
\begin{eqnarray}
E[X] &=& \theta \\
V[X] &=& \theta ( 1-\theta)
\end{eqnarray}
$$
期待値と分散の導出
期待値\(E[X]\)
確率変数\(X\)は0か1の2値なので、離散型の計算になります。
$$
\begin{eqnarray}
E[X] &=& \sum_{x=0}^1 x \cdot f(x|\theta)\\
&=& \sum_{x=0}^1 x \cdot \theta^x (1 – \theta)^{1-x} \\
&=& 0 \cdot \theta^0 (1-\theta)^{1} + 1 \cdot \theta^1(1-\theta)^{1-1} \\
&=& \theta
\end{eqnarray}
$$
分散 \(V[X]\)
$$
\begin{eqnarray}
V[X] &=& E[(X- E[X])^2] \\
&=& \sum_{x=0}^1 (x – \theta)^2 \cdot \theta^x (1-\theta)^{1-x} \\
&=& (0 – \theta)^2 \cdot \theta^0 ( 1- \theta){1-0} + (1 – \theta) ^2 \cdot \theta^1 (1-\theta)^{1-1}\\
&=& \theta^2 (1-\theta) + (1-\theta)^2 \theta \\
&=& (1-\theta) \left\{ \theta^2 + (1-\theta) \theta \right\} \\
&=& \theta ( 1- \theta)
\end{eqnarray}
$$

コメント