” これなら分かる最適化数学, 金谷健一 “で出てくる共役勾配法について数式上では納得できたのですが、これを図で書くと共役勾配な方向ってホントに解に向かう方向なの?という疑問がずっとありました。
ようやく納得する考え方が出来たので、ここで自分の考えをまとめます。正しいかどうか分かりませんが、分かりやすい助けにはなると思います。
共役勾配方向を図に書くと
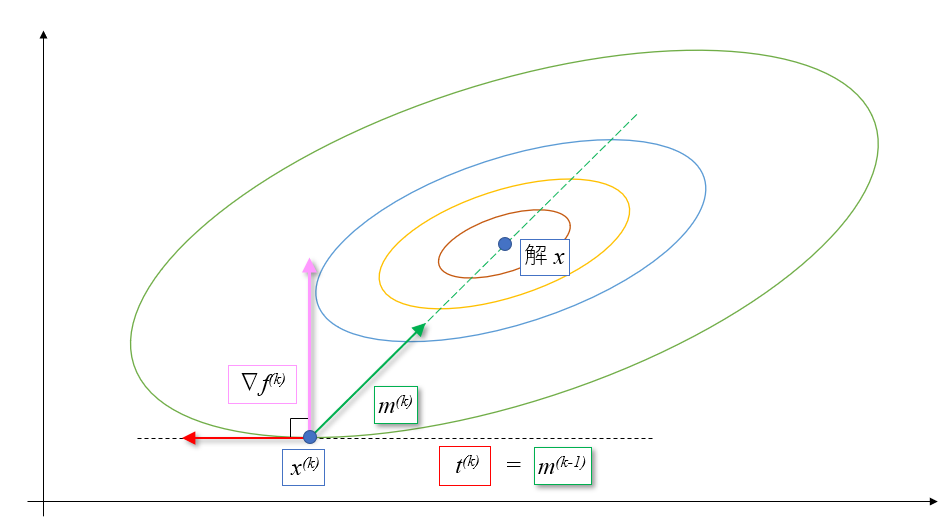
共役勾配な方向とは、近似解\(x ^{(k)}\)から解\(x\)に進むための方向で、勾配 \(∇f^{(k)}\)方向ではなく\( x – x^{(k)}\)に比例する\(m^{(k)}\)の方向です。
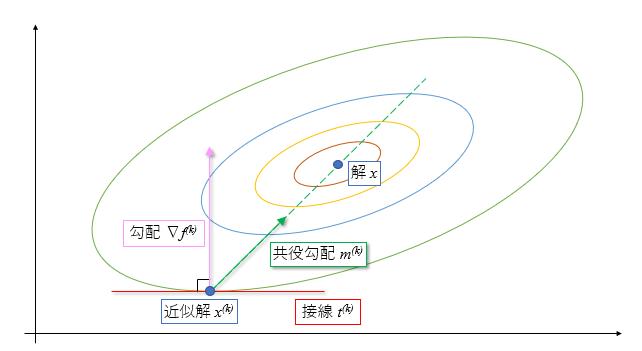
確かにこの図の方向\(m^{(k)}\)に進んでいけば解\(x\)に当たりますね。
“このような\(m^{(k)}\)は\( H^{(k)} m^{(k)} \propto \nabla f^{(k)} \)の関係があるので・・・”と本では続きますが、

ん? \(\nabla f^{(k)}\)に比例する方向って解の方向?
\(H^{(k)} m^{(k)} \)ってそもそもなんだっけ?
こんな疑問が湧いていました。
じゃあ、\(m^{(k)}\)の方向を描いて確かめてみましょう!
共役勾配な方向を計算
関数は2変数で考えます、つまり\(f(x,y)\)です。
まず共役であるとは、\( (t^{(k)}, H^{(k)} m^{(k)}) = 0\)の関係があるので、これを利用して\(m^{(k)}\)を計算してみます。
まず 接線 \(t^{(k)}\)は関数f(x,y)での点\(x^{(k)}\)で勾配\(\nabla f^{(k)}\)と直行する関係があります。 点\(x^{(k)}\)で勾配\(\nabla f^{(k)}\) は計算できるので、\(t^{(k)}\)は\(\nabla f^{(k)}\)を90°回転させて作ります。
回転行列は以下の式なので、
$$
R(\theta) = \left( \begin{array}{cc} cos(\theta) & -sin(\theta) \\ sin(\theta) & cos(\theta) \end{array} \right)
$$
ここから\(t^{(k)}\)は(1)式で計算できます。
$$
t^{(k)} = \left( \begin{array}{c} t_1 \\ t_2 \end{array} \right)
= R(90) \nabla f^{(k)} = \left(\begin{array}{cc} 0 & -1 \\ 1 & 0 \end{array}\right) \left(\begin{array}{cc}\partial f^{(k)} / \partial x \\ \partial f^{(k)} / \partial y \end{array}\right) = \left(\begin{array}{c} – \partial f^{(k)} / \partial y \\ \partial f^{(k)} / \partial x \end{array}\right) \tag{1}
$$
\(H^{(k)}\)は
$$
H^{(k)} = \left(\begin{array}{cc} H_{11} & H_{12} \\ H_{21} & H_{22} \end{array}\right) =
\left(\begin{array}{cc} \partial ^2 f^{(k)}/\partial x \partial x & \partial f^{(k)} / \partial x \partial y \\
\partial ^2 f^{(k)}/\partial y \partial x & \partial f^{(k)} / \partial y \partial y \end{array}\right)
$$
で、\(m^{(k)}\)は
$$
m^{(k)} = \left( \begin{array}{c} m_1 \\ m_2 \end{array} \right)
$$
とします。
\(m^{(k)}\)を求めたいので、\( (t^{(k)}, H^{(k)} m^{(k)}) = 0\)に\(t^{(k)}、H^{(k)}\)を代入して計算すると、
$$
m_2 = \frac{t_1 H_{11} + t_2 H_{12}}{t_1 H_{21} + t_2 H_{22}} m_1
$$
という\(m^{(k)}\)の算出ができます。つまり、\(m_1\)を適当に決めると\(m_2\)が決まるという関係ですね。
ここまで出てきた関係で、\(接線:t^{(k)} 、勾配:\nabla f^{(k)}、共役勾配な方向:m^{(k)}\)を描いてみましょう。
具体的な関数で共役勾配な方向を描く
例1:単純な楕円関数
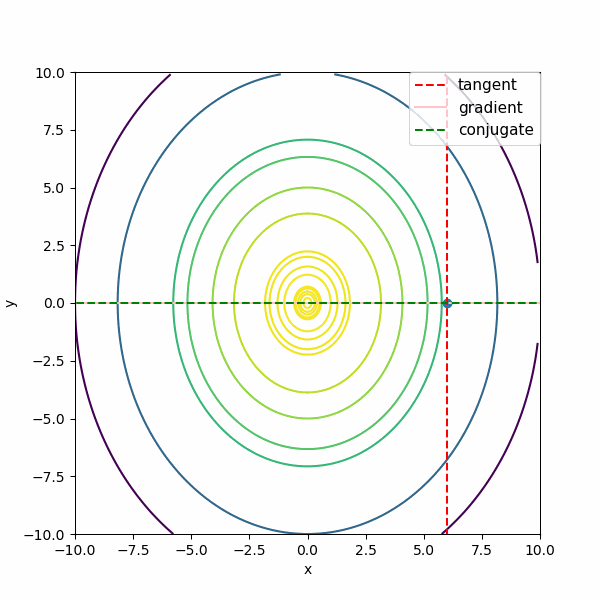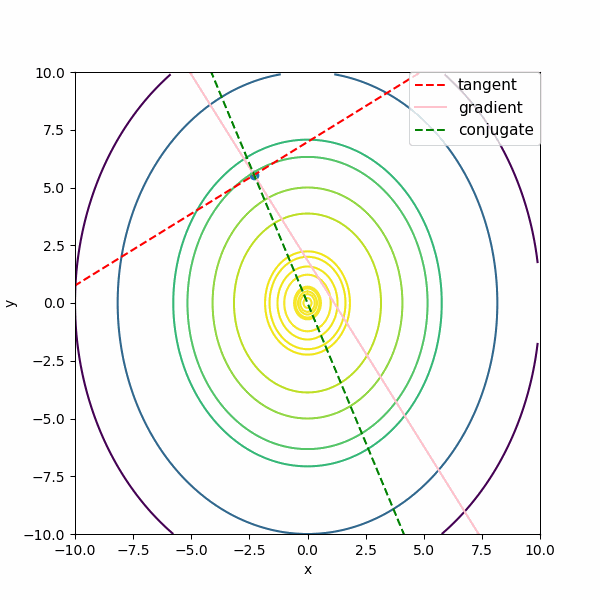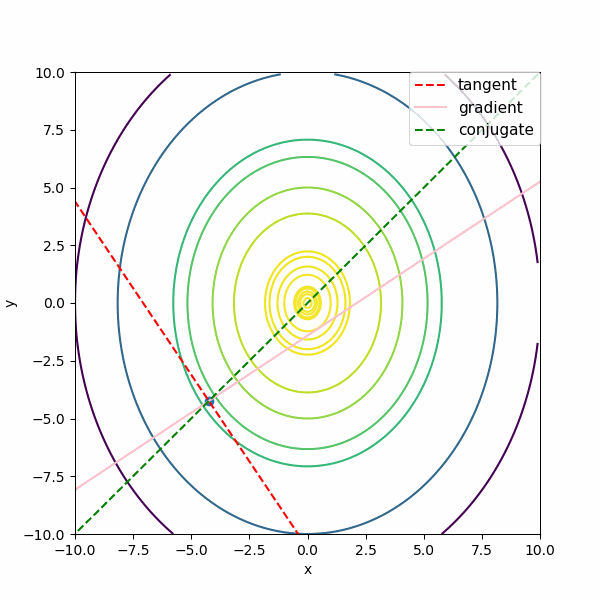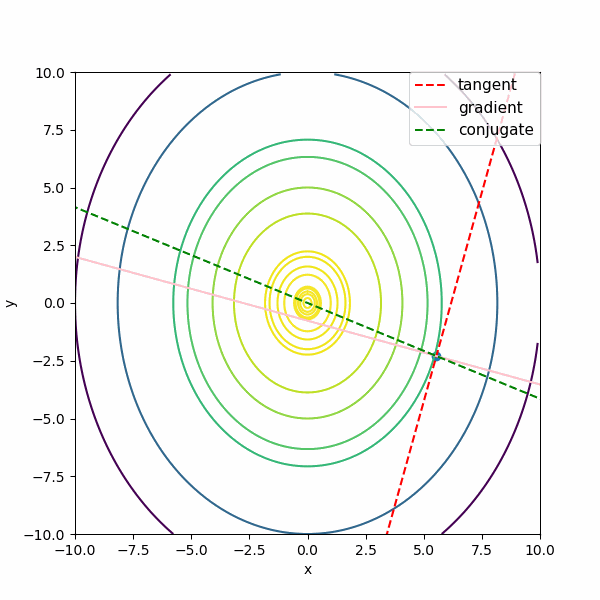
まず \(f(x,y) = -3 x^2 -2 y^2\)の単純な形で \(t^{(k)} 、\nabla f^{(k)}、m^{(k)}\)を描きます。
図では がtangent:接線 \(t^{(k)} \) 、gradient:勾配 \(\nabla f^{(k)}\) 、conjugate:共役勾配な方向 \(m^{(k)}\) です。描いている方向の長さは単位ベクトルではなく、適当な長さにしています。
ポイントを変えながら描いていますが、共役勾配な方向(conjugate:緑の点線)はどのポイントでも確かに極値(0,0)の方向に向いていますね。
例2:歪んでいる楕円関数
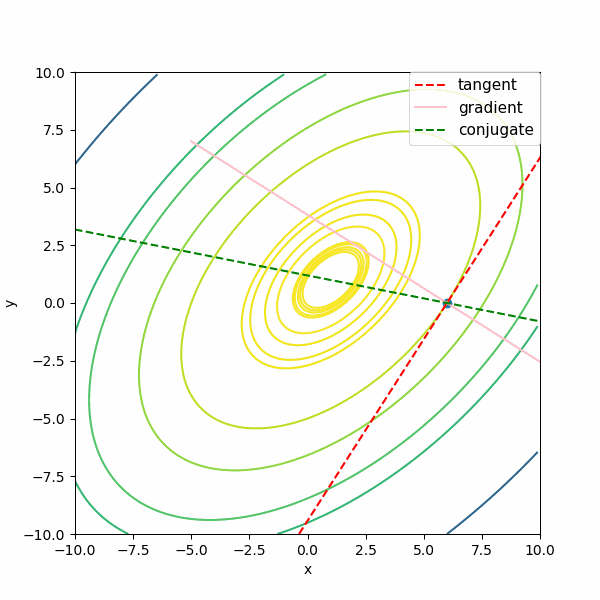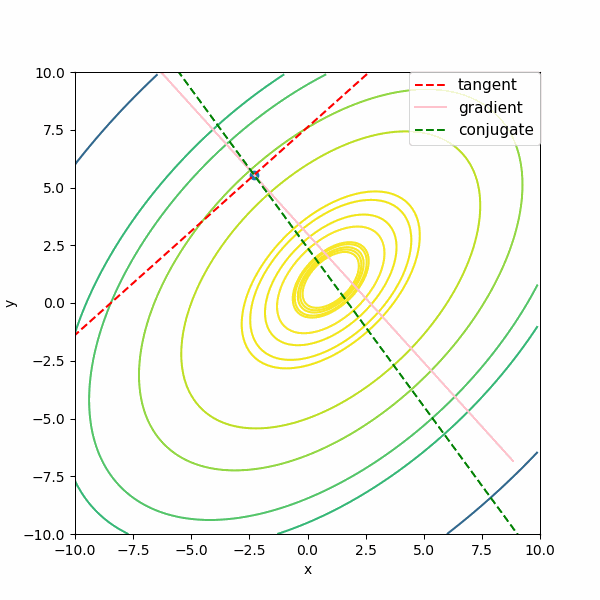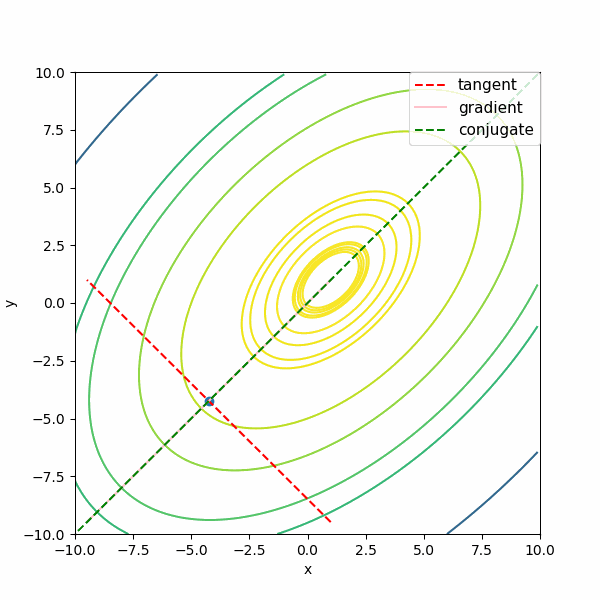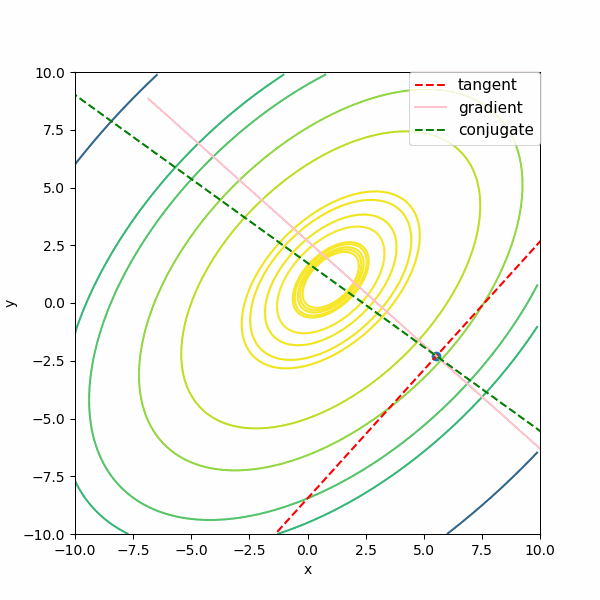
次は、\(f(x,y) = -x^2 + xy – y^2 + x + y\)の関数で、それぞれを描いてみます。例1よりも接線(tangent)と勾配(gradient)がいろいろな方向を向いていますが、共役勾配な方向(conjugate:緑の点線)は極値の方向を常に向いていますね。
この図でも、共役勾配な方向とは確かに極値を向いている方向だということが分かります。
例3:3次関数
次は\( f(x,y) = x^3 + y^3 -9 xy + 27 \)の3次関数で描いています。この関数はニュートン法を多変数に適用したときと同じものですね。
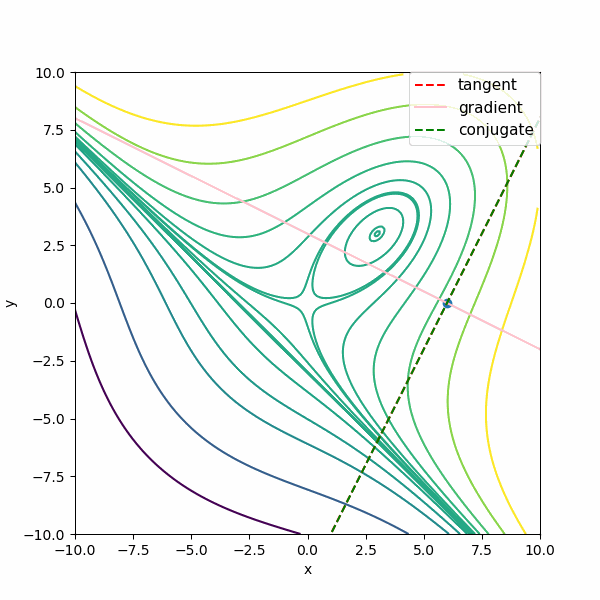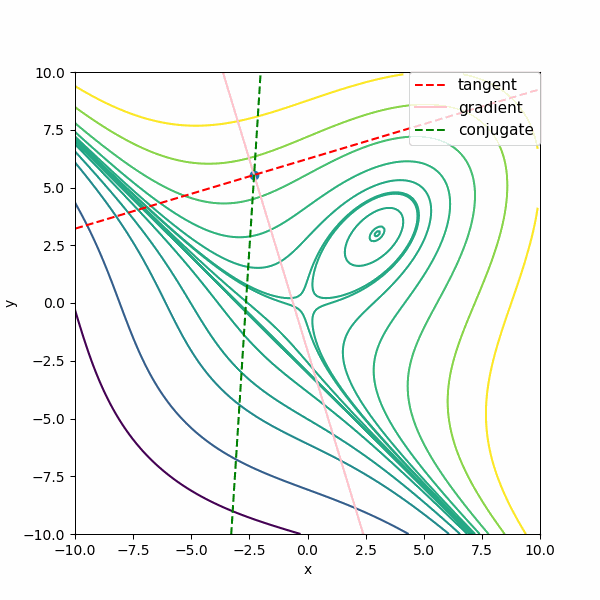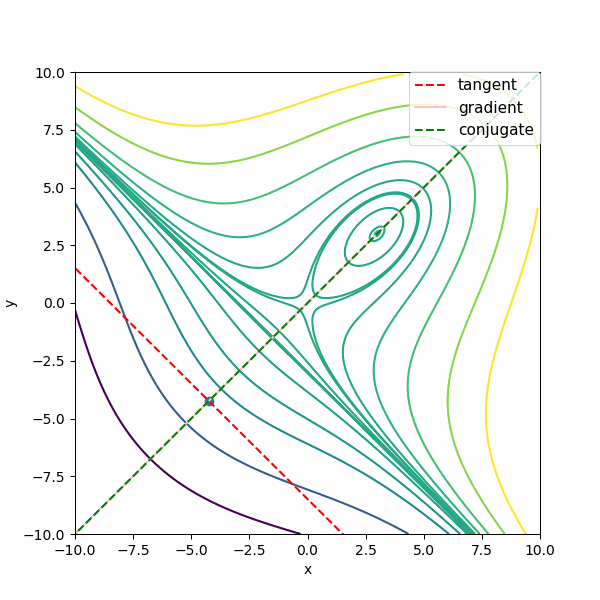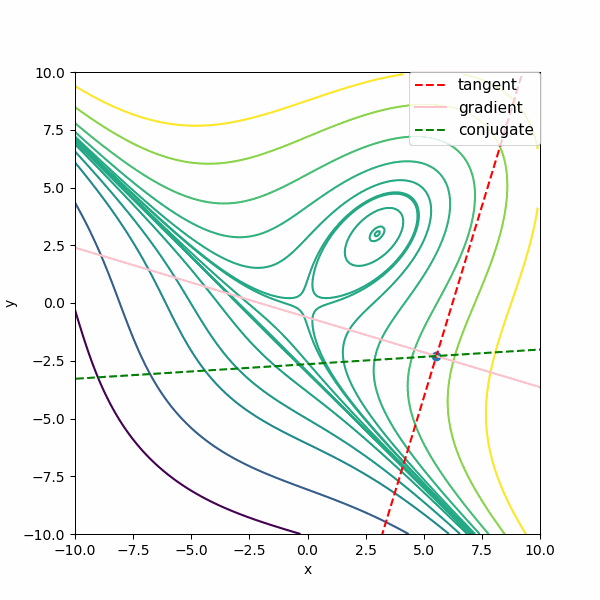

あれ?共役勾配な方向が極値の方向になっていないぞ?
これはいったい・・・
図形における共役勾配な方向とは
共役勾配な方向 は2次関数(例1、例2)の場合どのポイントでも極値を向いていましたが、3次関数(例3)の場合は常に極値を向いていませんでしたね。この結果が示すことって何なのでしょうか?
ここで接線、勾配、共役勾配な方向を描いているポイント、つまり\(x^{(k)}\)では(2)式の関係がありますね。
$$
(t^{(k)}, \nabla f^{(k)}) = 0 \tag{2}
$$
それから、(3)式の共役勾配な関係もありますね。
$$
(t^{(k)}, H^{(k)} m^{(k)}) = 0 \tag{3}
$$
(2)式と(3)式の関係から(4)式の関係があり、これってつまり、ニュートン法で、収束させる方向\(\Delta x\)を\(H \Delta x = – \nabla f \)から求めることと同じ関係だという事ですね。
$$
H^{(k)} m^{(k)} = \nabla f^{(k)} \tag{4}
$$
ここから\(m^{(k)}\)の方向は関数\(f\)の2次近似関数\(f_{II}\)の極値方向だという事が分かります。実際に例1、例2は2次関数なので \(m^{(k)}\) は常に極値を向いています。ニュートン法でも2次の場合はすぐに極値へ収束していますよね。でも例3の3次関数の場合はニュートン法でも収束に時間がかかったはずです。

つまり、共役勾配法とは
共役勾配法は極値を求める\(m^{(k)}\)の方向を 、ニュートン法のように\( m^{(k)} = H^{(k)-1}\nabla f^{(k)} \)の逆行列を計算して求めるのではなく、 \( m^{(k)} = \nabla f^{(k)} + \alpha ^{(k)} t^{(k)} \)で計算する方法ということが分かります。
この考え方を踏まえて、実際に共役勾配法を実装してみましょう。

コメント
[…] Keiさんのブログ […]