勾配法などで極値を見つける場合、そもそも極値が存在しているのかを気にする必要があります。ここで凸関数という考え方が出てきますが、その定義を見るとなぜこの定義?ということを考えてしまいます。定義なので”そういうものだ”と言われてしまうとそうなのですが、これをなぜこの定義になるのか図でイメージしながら考えみます。
凸関数の定義
凸関数は次のように定義されています。
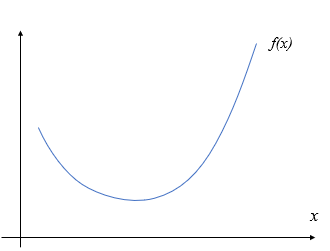
下に凸な関数の定義
$$
f\bigl(\alpha x_1 + (1-\alpha) x_2\bigr) \leq \alpha f(x_1) + (1-\alpha) f(x_2), 0 \leq \alpha \leq 1 \tag{1}
$$
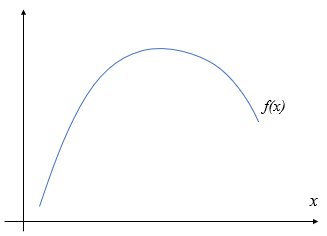
上に凸な関数の定義
$$
f\bigl(\alpha x_1 + (1-\alpha) x_2\bigr) \geq \alpha f(x_1) + (1-\alpha) f(x_2), 0 \leq \alpha \leq 1 \tag{2}
$$
(1)式、(2)式を見てもなんだこれ?ってなりませんか?
これは内分点という考え方から導かれるものです。
内分点
下の図のように\(x\)軸上に\(x_1\)と\(x_2\)があり、この2点間に存在している\(x_{1-2}\)を定義したいとします。
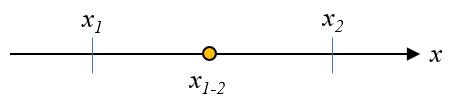
まず、\(x_2 > x_1\)より\(x_2\)は(3)式のようにできます。
$$
x_2 = x_1 + (x_2 – x_1) \tag{3}
$$
(3)式は、\(x_1\)に\(x_2\)と\(x_1\)の差分を加えるという考え方なので、これを図に描くと、青い帯の\(x_1\)に黄色い帯の\(x_2 – x_1\)が足されたものと考えることが出来ます。
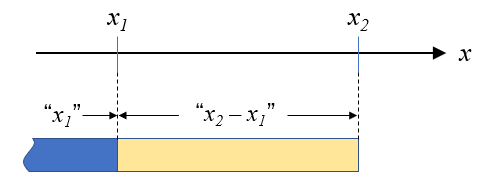
\(x_{1-2}\)が\(x_1\)と\(x_2\)のちょうど真ん中にあるとすると、黄色い帯の長さを半分にすれば
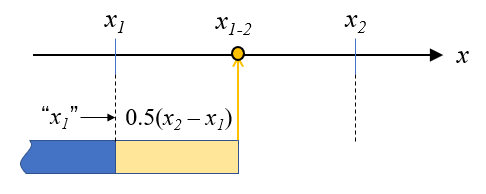
このような形で\(x_{1-2}\)を求めることができます。これは(4)式で表すことが出来ます。
$$x_{1-2} = x_1 + 0.5(x_2 – x_1) \tag{4}$$
内分点の式
\(x_{1-2}\)は\(x_1\)から\(x_2\)の間にあるので、黄色い帯の長さを\(0\) から\( 1\)とすれば内分点を表すことが出来ます。この係数を\(t\)とすると(5)式となります。
$$
x_{1-2} = x_1 + t(x_2 – x_1), 0 \leq t \leq 1 \tag{5}
$$
この式を\(x_1, x_2\)でまとめると(6)式となり
$$
x_{1-2} = (1 – t) x_1 + t x_2, 0 \leq t \leq 1 \tag{6}
$$
さらに、\(\alpha = 1 – t\)とすると、(7)式となり、これが内分点の式となります。
$$
x_{1-2} = \alpha x_1 + (1-\alpha) x_2, 0 \leq \alpha \leq 1 \tag{7}
$$
この内分点の考え方を関数に適用します。まずは下に凸な関数です。
下に凸な関数の内分点
下に凸な関数を描くと青いラインとなります。このグラフのx軸上に\(x_1,x_2\)を置いて、それぞれの\(f(x)\)である\(f(x_1), f(x_2)\)は縦軸上にプロットされます。
この縦軸上で\(f(x_1)\)と\(f(x_2)\)の間にある内分点\(y_{1-2}\)を定義していきます。この点\(y_{1-2}\)は\(f(x)\)の形とは関係がなく、 \(f(x_1)\)から\(f(x_2)\)の間で直線的に変化する値であることに注意してください。
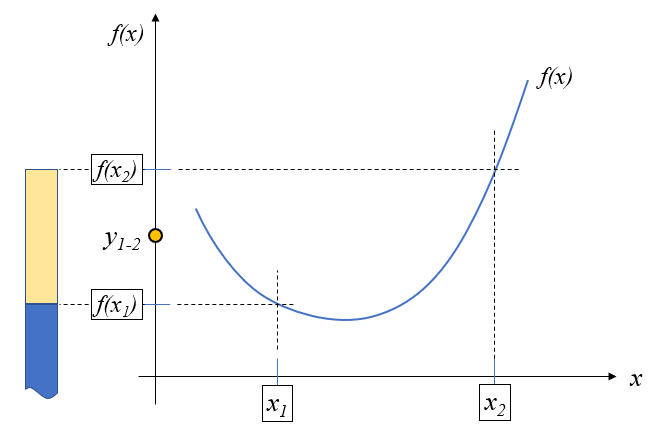
内分点\(y_{1-2}\)は先ほどx軸上で定義したように、(8)式になります。
$$
\begin{eqnarray}
y_{1-2} &=& f(x_1) + t \bigl( f(x_2) – f(x_1) \bigr), 0 \leq t \leq 1 \\
&=& (1- t) f(x_1) + t f(x_2) , 0 \leq t \leq 1 \tag{8}
\end{eqnarray}
$$
\(\alpha = 1 – t\)とすると、 (8)式は(9)式になります。
$$
y_{1-2} = \alpha f(x_1) + (1 – \alpha) f(x_2) , 0 \leq \alpha \leq 1 \tag{9}
$$
この(9)式を内分点とします。
下に凸な関数の定義を図に描く
(7)式、(9)式を\(x_{1-2} \propto \alpha, y_{1,2} \propto \alpha\)として、関数上に描くと黄色いラインが描けます。 \(x_{1-2}\)に対する\(y_{1-2}\)は黄色の点です。 \(f(x)\)の\(x_{1-2}\)の値\(f(x_{1-2})\)は青い点で描くことが出来ます。
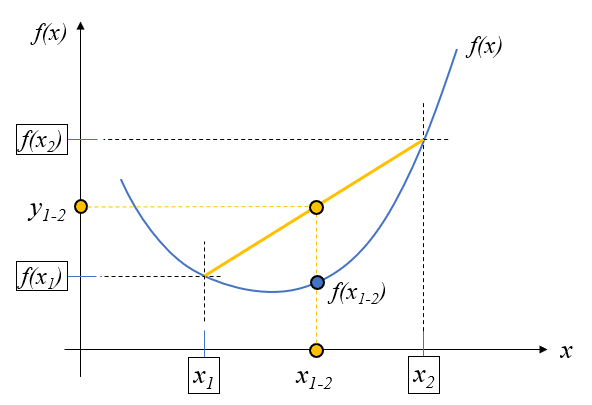
この図の関係より、\(f(x_{1-2}) \leq y_{1-2}\)であることが分かります。この式に(7)式、(9)式を代入すると(10)式となり、これは(1)式と一緒なので、定義を導くことが出来ました。
$$
f \bigl( \alpha x_1 + (1-\alpha) x_2 \bigr) \leq \alpha f(x_1) + (1-\alpha) f(x_2), 0 \leq \alpha \leq 1 \tag{10}
$$
こんな感じで内分点を図に描くと、なんで凸関数がこんな定義になっているのか分かりますね!
下に凸な関数の定義を図に描けたので、上に凸な関数の定義を図に描いてい見ます。
上に凸な関数の定義を図に描く
横軸と縦軸の内分点の関係は変わらないので、上に凸な関数\(f(x)\)の\(x_1,x_2\)に対する\(f(x_1), f(x_2)\)、そして\(y_{1-2}\)は図の黄色のラインで描くことが出来ます。
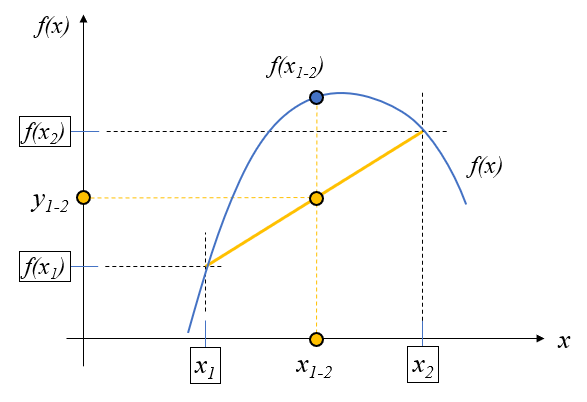
この図より\(f(x_{1-2}) \geq y_{1-2}\)であることが分かるので、(7)式、(9)式を適用すると、(11)式となり、(2)式と一致します。
$$
f \bigl( \alpha x_1 + (1-\alpha) x_2 \bigr) \geq \alpha f(x_1) + (1-\alpha) f(x_2), 0 \leq \alpha \leq 1 \tag{11}
$$
内分点を図に描くことで上に凸な関数の定義を図で理解することが出来ました。
この凸関数の定義を使えば、勾配法で最大値を探すか最小値を探すかを判断することや、黄金分割法の考え方を導くときに使うことができます。
コメント