” これなら分かる最適化数学, 金谷健一 “の ニュートン法を多変数関数に適用して極値を探してみます。1変数のニュートン法は綺麗に収束していきましたが、多変数だとどうなるでしょうか。
多変数の場合のニュートン法アルゴリズム
以前の記事で示したように、多変数関数\(f(x_1,\cdots,x_n)\)を勾配\(\nabla \bar f\)とヘッセ行列\(\bar H\)で表すと(1)式の近似式になります。\(\nabla \bar f, \bar H\)はそれぞれ、\(\boldsymbol{\bar x}\)での勾配\(\nabla f\)とヘッセ行列\(H\)です。
$$
f(\boldsymbol{x}) \simeq \bar f + (\nabla \bar f, \boldsymbol{x – \bar x}) + \frac{1}{2}\Bigl( \boldsymbol{x – \bar x}, \bar H ( \boldsymbol{x – \bar x} ) \Bigr) \tag{1}
$$
$$
\boldsymbol{x} =(x_1, \cdots x_n), \boldsymbol{x – \bar x} = (x_1 – \bar x_1 , \cdots , x_n – \bar x_n)^T ,
\\
\nabla \bar f = \left(\begin{array}{c} \partial \bar f / \partial x_1 \\ \vdots \\ \partial \bar f / \partial x_n \end{array} \right) ,
\bar H = \left( \begin{array}{ccc} \partial^2 \bar f / \partial x_1 \partial x_1 & \cdots & \partial^2 \bar f / \partial x_1 \partial x_n \\ \vdots & \ddots & \vdots \\
\partial^2 \bar f / \partial x_n \partial x_1 & \cdots & \partial^2 \bar f / \partial x_n \partial x_n \end{array}\right)
$$
この(1)式を\(\boldsymbol{\Delta x} = (\boldsymbol{x – \bar x})\)で微分してゼロとします((2)式)。
$$
\nabla \bar f + \bar H \boldsymbol{\Delta x} = 0 \tag{2}
$$
この(2)式は”微分して=0”の関係なので、近似式である(1)式の極値となる\(\boldsymbol{\Delta x}\)をここから算出します。\(\boldsymbol{\Delta x} = \bar H ^{-1} \nabla \bar f\)として\(\bar H\)の逆行列を計算する方法でもできますが、多次元行列の逆行列を計算することはとても大変なので、(3)式の関係から \( \boldsymbol{\Delta x} \)を求めます。
$$
\bar H \boldsymbol{\Delta x} = \nabla \bar f \tag{4}
$$

(4)式からどうやって\(\boldsymbol{\Delta x}\)を計算するの?
って思った方がいるのではないかと思いますが、LU分解という方法で求めることが出来ます。
次に求めた\( \boldsymbol{\Delta x}\)を使い、解 \(\boldsymbol x\)を(5)式で計算します。
$$
\boldsymbol{x} = \boldsymbol{\bar x + \Delta x} \tag{5}
$$
これは近似式での解(極値)であるので、次の\(\boldsymbol{\bar x^{(k+1)} = x^{(k)}}\)として、\(\boldsymbol{\Delta x} < \sigma\)になるまで繰り返せば関数の極値が求まります。1変数のニュートン法と比べてみてください。変数が多くなっていますが、基本的には同じです。
\(\bar x\)の点で2次近似式で展開→その近似式の極値を求める→\(\bar x\)を更新→ \(\bar x\)の点で2次近似式で展開→その近似式の極値を求める→\(\bar x\)を更新→ \(\cdots\)を繰り返していけば、近似する元の関数の極値が求まるという考え方です。
実際に計算してみましょう
2変数の2次関数で計算
多変数の勾配法と同じ2変数の2次関数(6)式でニュートン法を実行してみます。
$$
f(x, y) = -5(x-1)^2 – 2(y – 2)^2 \tag{6}
$$
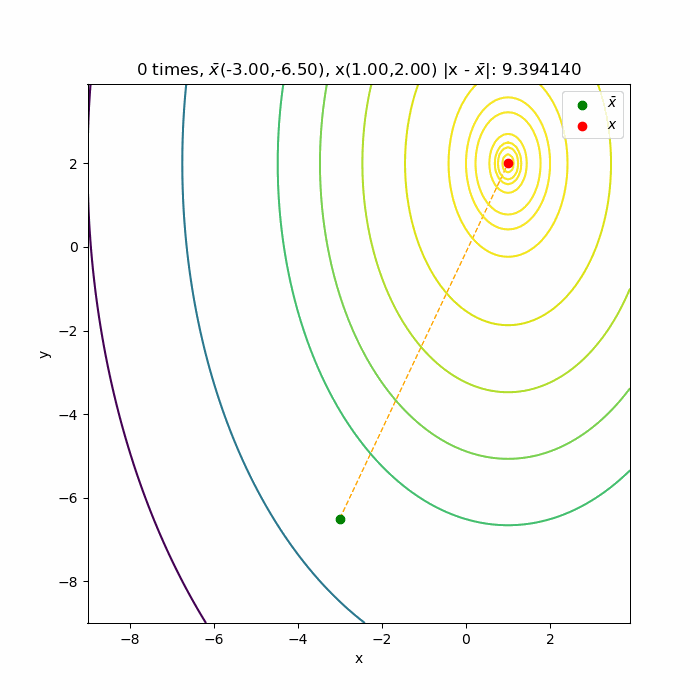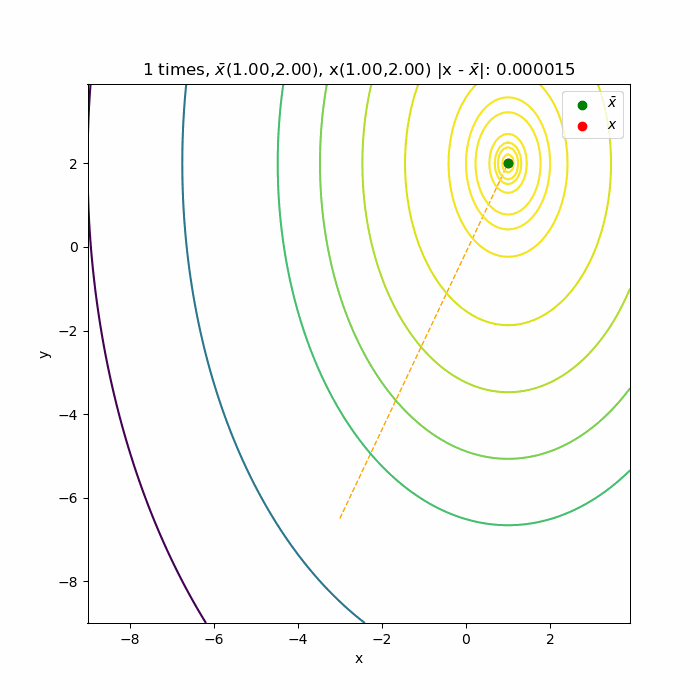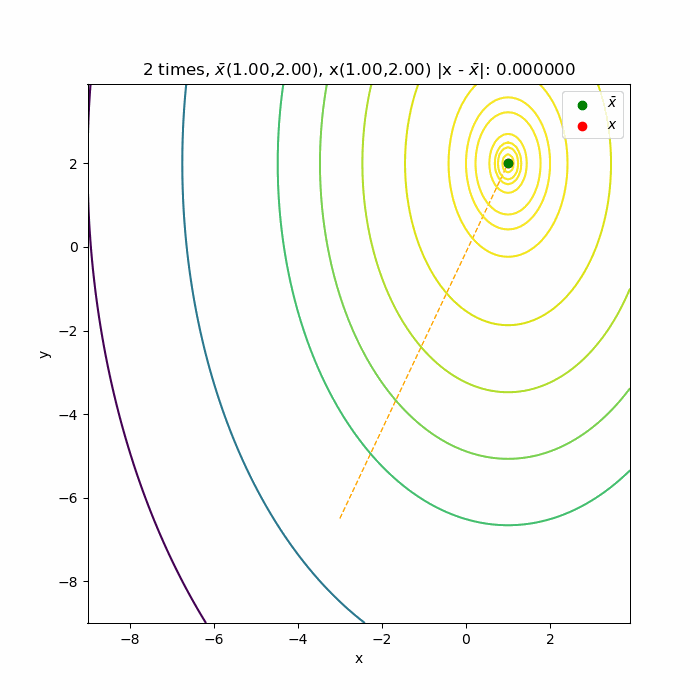
多変数の勾配法と違って1回目でほぼ関数の極値になっていますね。
なぜこんなに綺麗に極値がもとまっているのでしょう?
それは、極値を計算する(6)式が2次式であって、ニュートン法も2次近似式の極値を利用しているから、1回目の近似解が関数の極値になるからです。テイラー展開でも元の式のオーダーに近似式を合わせると同じ形になるのでしたよね。本当は1回目で極値へ到達するはずですが、数値計算誤差で収束に時間がかかっています。
こんな感じで、極値を求める式が2次式であれば素早く収束します。
2変数の3次関数で計算
次は(7)式で極値を計算してみます。
$$
f(x,y) = x^3 + y ^3 -9 xy + 27 \tag{7}
$$
そもそもこの関数はどんな形をしているのでしょうか?描いてみるとこんな感じです。メッシュと等高線を一緒に書いています。破線は関数の形が分かりやすいように、XY平面の対角上の関数値を描いたものです。大まかな形は、右上から左下に向かって下がり、ピンクの領域では下に凸な形ですね。中心付近が鞍点となっていて、ピンクの領域に停留点があるようです。
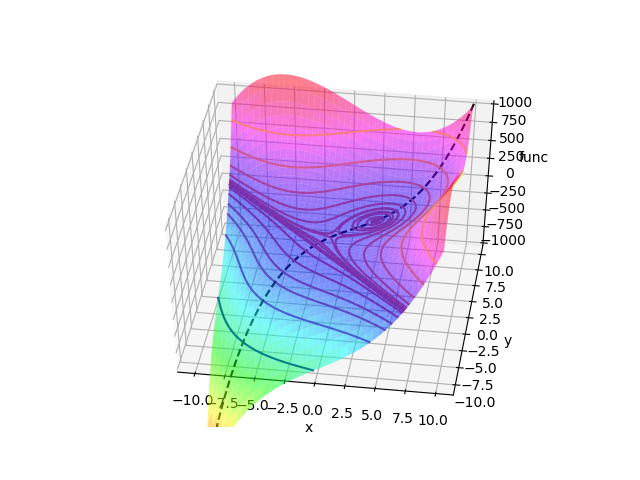
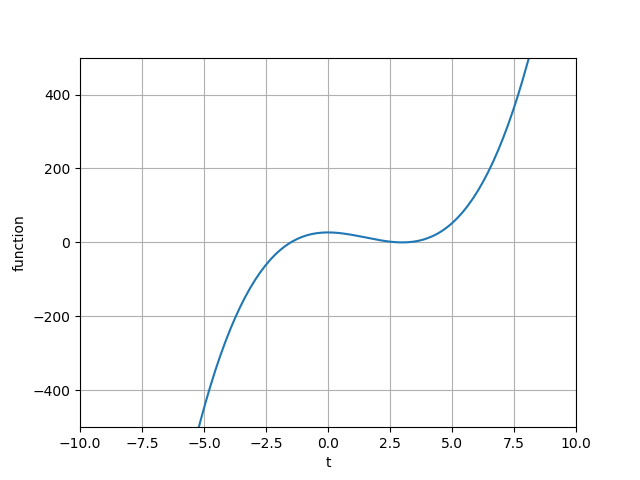
破線を平面に描くとこんな感じです。横軸\(t\)の方向は上の図の破線方向です。縦軸は上の軸と同じf(x,y)と同じです。この図からも”0″付近に鞍点があって、そこから右に行ったところに停留点があることが分かりますね。
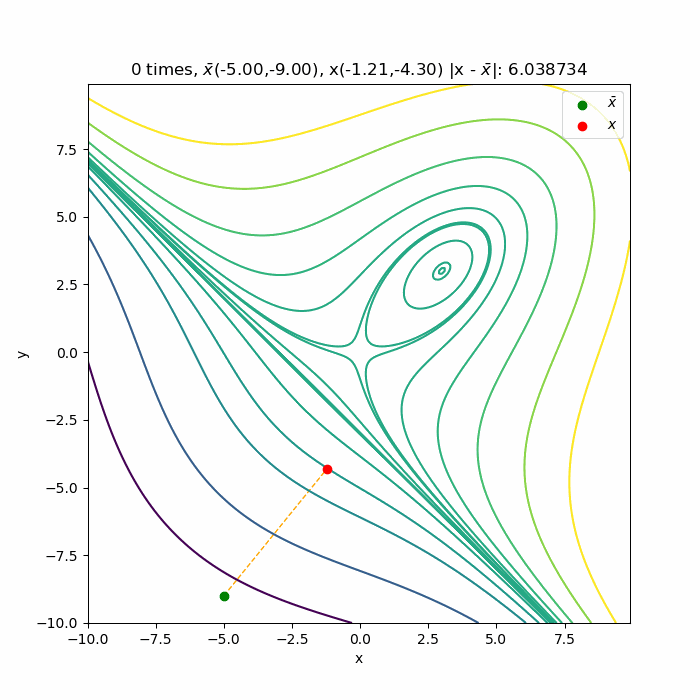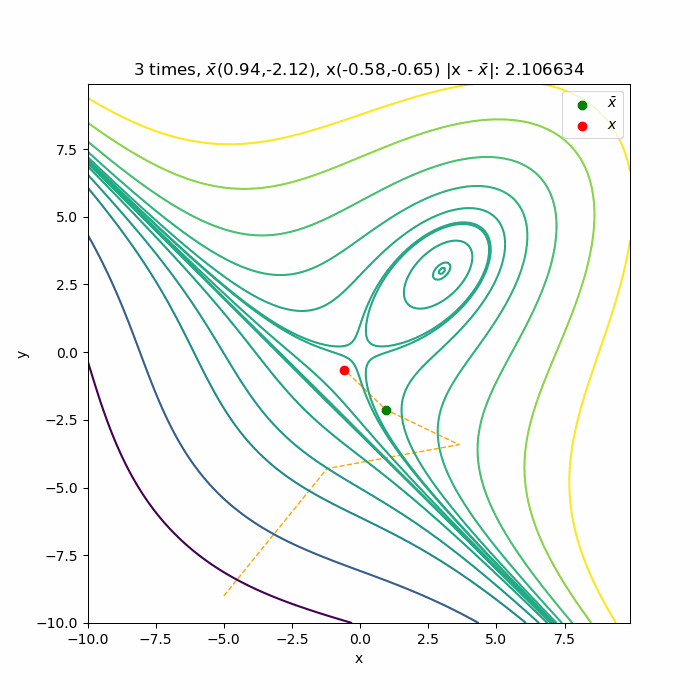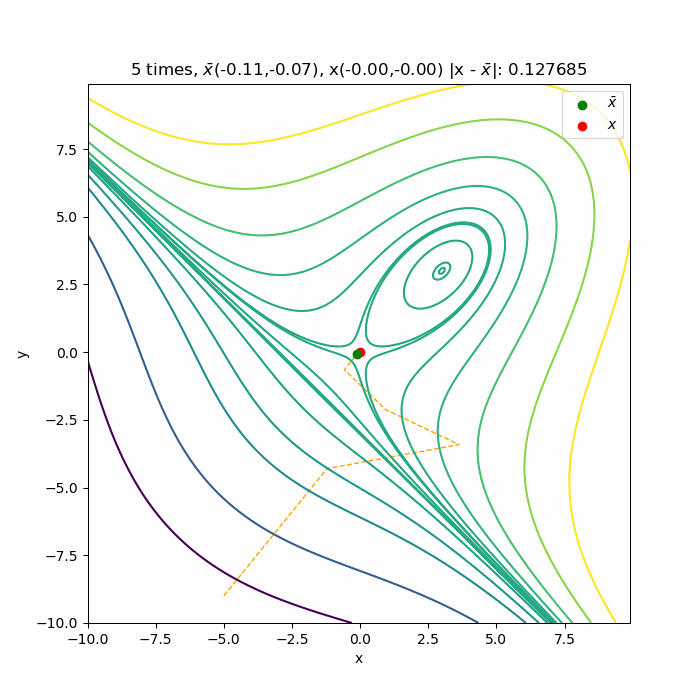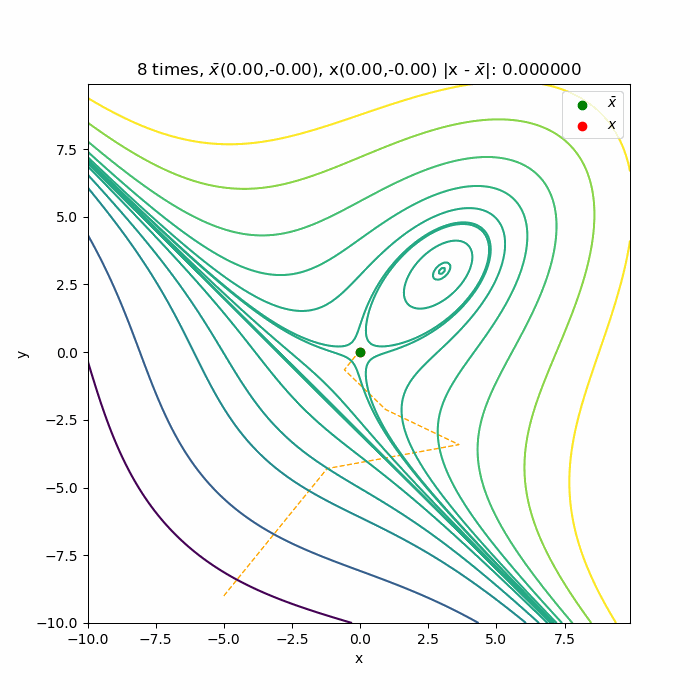
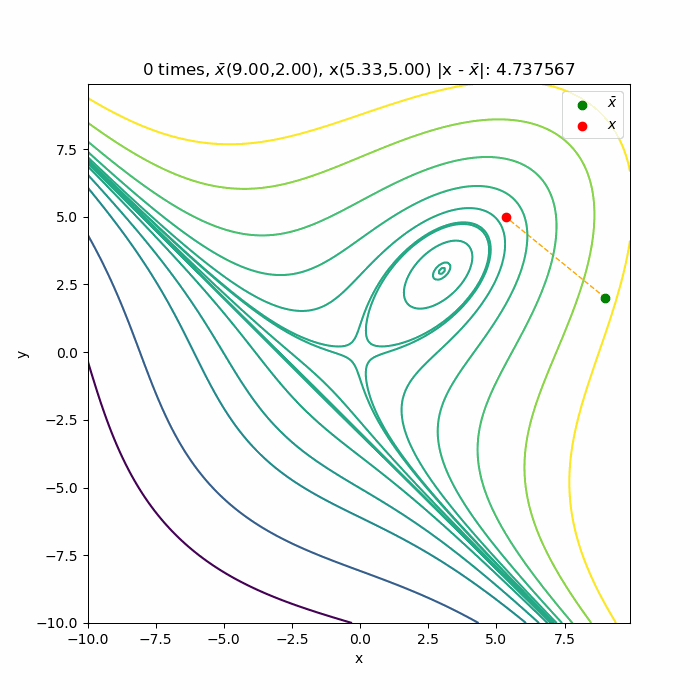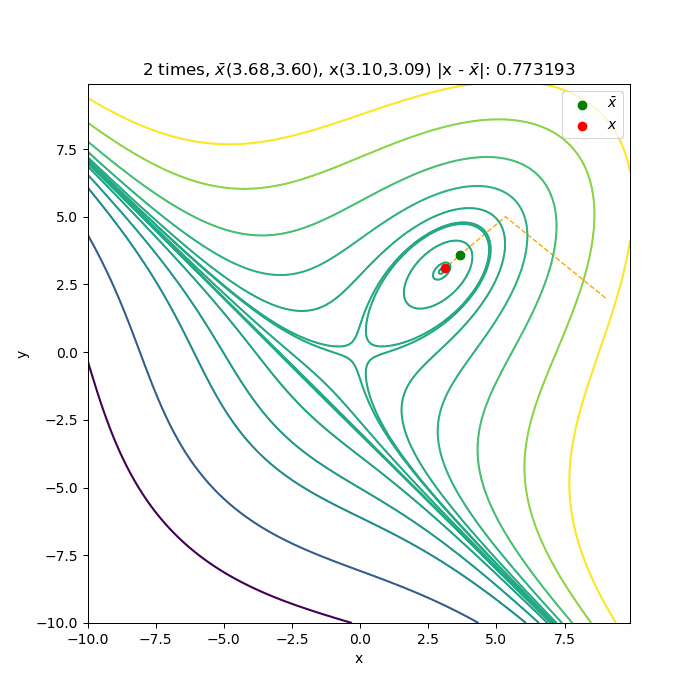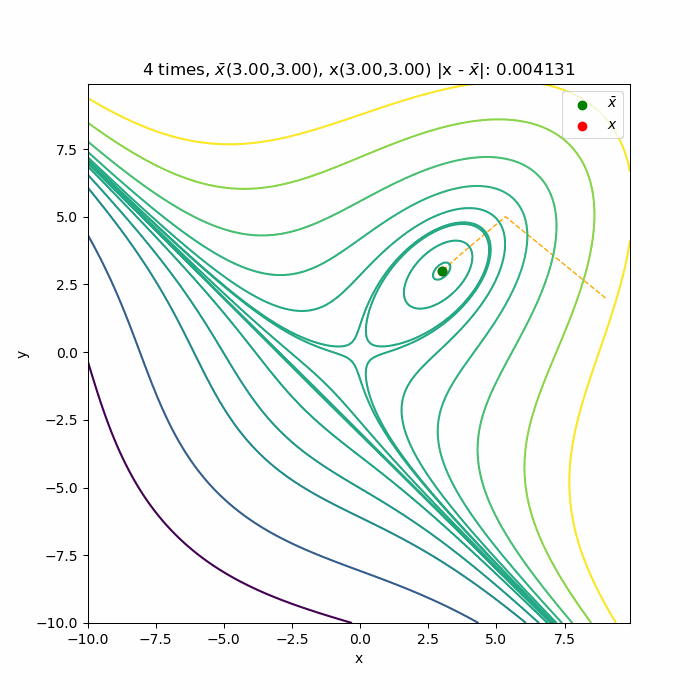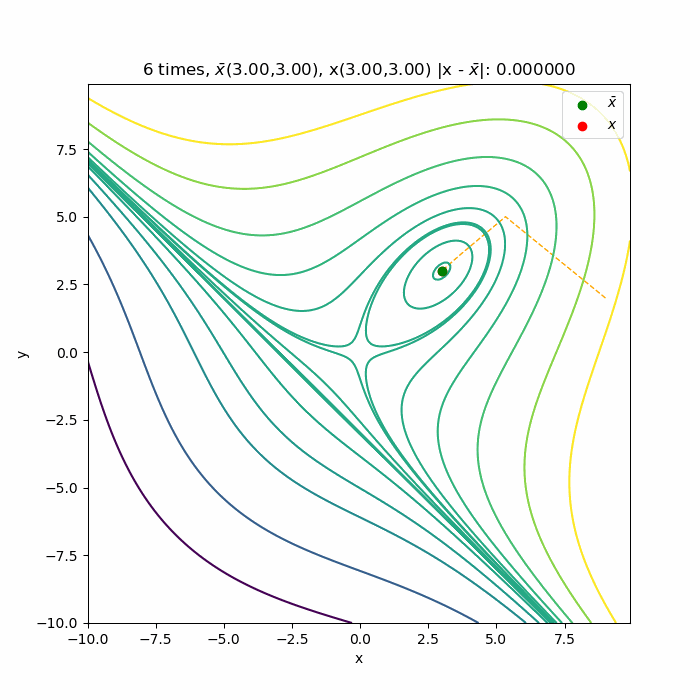
初期値\( (-5.0, 9.0) \)からの収束の様子です。最後は\(0.0,0.0)\)の鞍点へ収束しています。2次近似式の展開点 \( \bar x\)と、その近似式の極値 \( x \)を描いていますが、両者がだんだん近づいて行っていることで、徐々に収束していくことが分かります。
左上から右下に向かって伸びている直線を境に関数の形が変化していますが、それにも対応できています。
初期値\( (9.0, 2.0) \)からの収束の様子です 。停留点である( \(3.0, 3.0) \)へ収束していく様子が分かります。こちら側は下に凸な関数なので、綺麗に収束していっています。
以上ニュートン法を多変数に適用した場合でした。次は共役勾配法を記事にします。
ニュートン法は非線形最小二乗法などに適用することが出来ます。
ニュートン法のコード – Python
ニュートン法のクラス
import numpy as np
import scipy.linalg as linalg
class Newton:
def __init__(self, func):
self.func = func
self.delta_h = 0.00001
def d_func_dx(self, func, x, y):
return (func(x + self.delta_h, y) - func(x - self.delta_h, y)) / (2 * self.delta_h)
def d_func_dy(self, func, x, y):
return (func(x, y + self.delta_h) - func(x, y - self.delta_h)) / (2 * self.delta_h)
def nabla_f(self, x, y):
return np.array([self.d_func_dx(self.func, x, y), self.d_func_dy(self.func, x, y)])
def dd_func_dxdx(self, func, x, y):
return (self.d_func_dx(func, x + self.delta_h, y) - self.d_func_dx(func, x - self.delta_h, y)) / ( 2* self.delta_h)
def dd_func_dxdy(self,func, x, y):
return (self.d_func_dx(func, x, y + self.delta_h) - self.d_func_dx(func, x, y - self.delta_h)) / (2 * self.delta_h)
def dd_func_dydx(self, func, x, y):
return (self.d_func_dy(func, x + self.delta_h, y) - self.d_func_dy(func, x - self.delta_h, y)) / (2 * self.delta_h)
def dd_func_dydy(self, func, x, y):
return (self.d_func_dy(func, x, y + self.delta_h) - self.d_func_dy(func, x, y - self.delta_h)) / (2 * self.delta_h)
def hesse_H(self, x, y):
return np.array([[self.dd_func_dxdx(self.func, x, y), self.dd_func_dxdy(self.func, x, y)],
[self.dd_func_dydx(self.func, x, y), self.dd_func_dydy(self.func, x, y)]])
def search(self, initial_x, initial_y, sigma):
x = initial_x
y = initial_y
while True:
x_bar = x
y_bar = y
F = self.nabla_f(x_bar, y_bar)
H = self.hesse_H(x_bar, y_bar)
# LU分解でΔxを求める
LU = linalg.lu_factor(H)
delta_x = linalg.lu_solve(LU, -F)
# xの更新
x = x_bar + delta_x[0]
y = y_bar + delta_x[1]
norm = np.sqrt(np.sum(delta_x**2))
if norm < sigma:
break
return [x, y]
実行コード
# 関数の設定 (勾配法を同じ関数) function = lambda x,y : -5*(x-1)**2 - 2*(y-2)**2 # 初期値の設定 initial_x = -3 initial_y = -6.5 sigma = 0.000001 #収束条件 # ニュートン法のインスタンス newton = Newton(function) # ニュートン法による最適値探索 opt_x = newton.search(initial_x, initial_y, sigma)
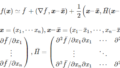

コメント