最小二乗法を使えばデータから係数を求めることが出来ます。今回はその例として、円のパラメータを最小二乗法でデータから求めてみます。
データから円のパラメータを推定しよう
円の方程式とパラメータ
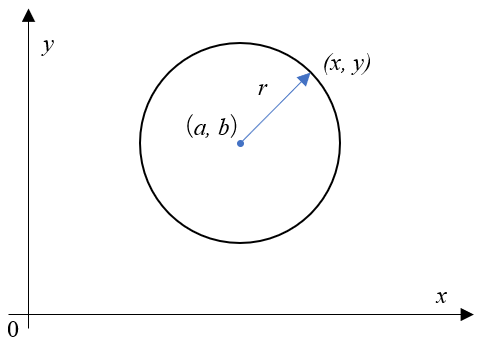
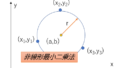
円の方程式は(1)式で、\((a,b)\)が円の中心、\(r\)が円の半径を表しています。
これは、\((a,b,r)\)の3つのパラメータがあれば、円のある点\(x,y)\)が求まるということを意味していますね。
$$
(x-a)^2 + (y-b)^2 = r^2 \tag{1}
$$
データからパラメータ
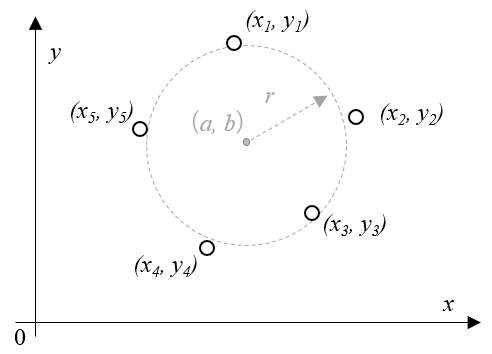
では、\((x_i,y_i), i \in (1,2,3,4,5)\)のデータがあるとき、この5つのデータから円の方程式のパラメータ\((a,b,r)\)を計算してみましょう。方法は最小二乗法です。
円のパラメータ推定のための最小二乗法
評価関数
円の方程式のパラメータ\((a,b,r)\)は、(2)式の評価関数\(J\)を最小にすることで求めることが出来ます。
$$
J = \frac{1}{2} \sum_{i=1}^{n} \bigl( (x_i – a)^2 + (y_i – b)^2 – r^2 \bigr) ^2 \rightarrow min \tag{2}
$$
最小二乗法で計算するには、データとパラメータが次のような一次多項式の形となっていないといけません。ここでは、\(x_i, y_i\)をデータ、\(a_i\)をパラメータとしています。
$$
a_0 x_i^n + a_1 x_i^{n-1} + \cdots + a_n – y_i
$$
ということで、(2)式の中身を展開していきましょう。
$$
\begin{eqnarray}
(x_i – a)^2 + (y_i – b)^2 – r^2 &=& x_i^2 – 2a x_i + a^2 + y_i^2 -2b y_i +b^2 – r^2 \\
&=& x_i^2 + y_i^2 – 2a x_i -2b y_i + a^2 +b^2 – r^2 \tag{3}
\end{eqnarray}
$$
評価関数\(J\)の中身の式が(3)式のように展開出来ました。この式は求めたいパラメータ\((a,b,r)\)の2乗があるので、微分してもパラメータが消えてくれません。
そこで、パラメータが一次多項式の形になるように(4)式のように\((\alpha, \beta, \gamma)\)を決めます。
$$
\begin{eqnarray}
\alpha &=& -2a \\
\beta &=& -2b \\
\gamma &=& a^2 +b^2 – r^2
\end{eqnarray} \tag{4}
$$
こうすることで、評価関数\(J\)の中身は(5)式のようになり、最小二乗法で計算できる一次多項式の形になりました。

めでたし
めでたし
$$
x_i^2 + y_i^2 + \alpha x_i + \beta y_i + \gamma \tag{5}
$$
改めて円のパラメータを求めるための評価関数\(J\)は(6)式となります。
$$
J = \frac{1}{2} \sum_{i=1}^{n} \bigl( x_i^2 + y_i^2 + \alpha x_i + \beta y_i + \gamma \bigr) ^2 \tag{6}
$$
正規方程式の導出
まず求めるパラメータは\((\alpha, \beta, \gamma)\)なので、評価関数\(J\)をこのそれぞれで微分してゼロとおきます。
$$
\begin{eqnarray}
\frac{\partial J}{\partial \alpha} &=& \sum_{i=1}^{n} x_i \bigl( x_i^2 + y_i^2 + \alpha x_i + \beta y_i + \gamma \bigr) =0 \\
\frac{\partial J}{\partial \beta} &=& \sum_{i=1}^{n} y_i \bigl( x_i^2 + y_i^2 + \alpha x_i + \beta y_i + \gamma \bigr) = 0 \\
\frac{\partial J}{\partial \gamma} &=& \sum_{i=1}^{n} \bigl( x_i^2 + y_i^2 + \alpha x_i + \beta y_i + \gamma \bigr) = 0
\end{eqnarray} \tag{7}
$$
次に既知のデータだけの項\((x_i, y_i)\)を右辺に、そして求めたい\((\alpha, \beta, \gamma)\)を含む項を左辺にまとめます。
$$
\begin{eqnarray}
\sum_{i=1}^{n} \bigl( \alpha x_i^2 + \beta x_i y_i + \gamma x_i \bigr) &=& -\sum_{i=1}^{n} x_i \bigl( x_i^2 + y_i^2 \bigr) \\
\sum_{i=1}^{n} \bigl( \alpha x_i y_i + \beta y_i^2 + \gamma y_i \bigr) &=& -\sum_{i=1}^{n} y_i \bigl( x_i^2 + y_i^2 \bigr) \\
\sum_{i=1}^{n} \bigl( \alpha x_i + \beta y_i + \gamma \bigr) &=& -\sum_{i=1}^{n} \bigl( x_i^2 + y_i^2 \bigr)
\end{eqnarray} \tag{8}
$$
これを行列の形で表すと(9)式になります。
$$
\left(\begin{array}{lll}
\sum_{i=1}^{n} x_i^2 & \sum_{i=1}^{n} x_i y_i & \sum_{i=1}^{n} x_i \\
\sum_{i=1}^{n} x_i y_i & \sum_{i=1}^{n} y_i^2 & \sum_{i=1}^{n} y_i \\
\sum_{i=1}^{n} x_i & \sum_{i=1}^{n} y_i & \sum_{i=1}^{n} 1
\end{array}\right)
\left(\begin{array}{c}
\alpha \\ \beta \\ \gamma
\end{array}\right) =-\left(\begin{array}{l}
\sum_{i=1}^{n} x_i \bigl( x_i^2 + y_i^2) \\
\sum_{i=1}^{n} y_i \bigl( x_i^2 + y_i^2) \\
\sum_{i=1}^{n} \bigl( x_i^2 + y_i^2)
\end{array}\right) \tag{9}
$$
これで正規方程式が導出できました。この式は\(\boldsymbol{A} \boldsymbol{x} = \boldsymbol{b}\)の形になっているので、LU分解などで\((\alpha, \beta, \gamma)\)を求めることが出来ます。
\((\alpha, \beta, \gamma)\)から\((a,b,r)\)を求める
正規方程式から\((\alpha, \beta, \gamma)\)を求めることが出来ます。(4)式のように \((\alpha, \beta, \gamma)\) と\((a,b,r)\)が決まっているので、ここから(10)式の計算できます。
$$
\begin{eqnarray}
\alpha = -2a &\Rightarrow& a = – \alpha /2\\
\beta = -2b &\Rightarrow& b = – \beta / 2\\
\gamma = a^2 +b^2 – r^2 &\Rightarrow& r^2 = a^2 + b^2 – \gamma
\end{eqnarray} \tag{10}
$$
この(10)式で\(r\)を平方根の計算をしてもいいでしょうか?\( a^2 + b^2 – \gamma \)がマイナスになっている場合、平方根を取ったら虚数になってしまいますね。
でももともと円の方程式は\(r^2 = (x-a)^2 + (y-b)^2\)という形となっているので、常に\(r\)はプラスとなります。そこで \( a^2 + b^2 – \gamma \) の絶対値の平方根を計算して\(r\)を求めるようにします。
以上で円の方程式のパラメータを求める方法を導出しました。これをプログラムを書いて計算してみます。
Pythonで円のパラメータを最小二乗法で求める
ポイントデータの作成
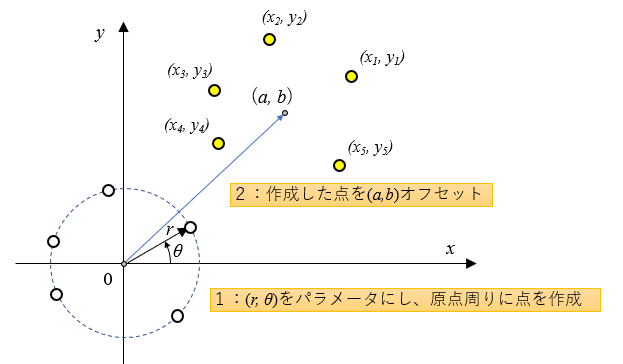
まず、\((a,b,r,\theta)\)のパラメータを使って5つのポイントデータを作成します。この方法では円からのずれがないポイントデータが作成されるので、このポイントデータを使って最小二乗法で\(a,b,r)\)を求めると上記のパラメータ値と同じになるはずです。
import math
import numpy as np
r = 20.0
a = 10.0
b = 15.0
thetas = [0.0, 45.0, 100.0, 200.0, 270.0]
point = []
for theta in thetas:
point.append([r*math.cos(math.radians(theta))+a, r*math.sin(math.radians(theta))+b])
正規方程式の項を計算
$$
\left(\begin{array}{lll}
\sum_{i=1}^{n} x_i^2 & \sum_{i=1}^{n} x_i y_i & \sum_{i=1}^{n} x_i \\
\sum_{i=1}^{n} x_i y_i & \sum_{i=1}^{n} y_i^2 & \sum_{i=1}^{n} y_i \\
\sum_{i=1}^{n} x_i & \sum_{i=1}^{n} y_i & \sum_{i=1}^{n} 1
\end{array}\right)
\left(\begin{array}{c}
\alpha \\ \beta \\ \gamma\end{array}\right) = -\left(\begin{array}{l}
\sum_{i=1}^{n} x_i \bigl( x_i^2 + y_i^2) \\
\sum_{i=1}^{n} y_i \bigl( x_i^2 + y_i^2) \\
\sum_{i=1}^{n} \bigl( x_i^2 + y_i^2) \\
\end{array}\right)
$$
次に\(\alpha, \beta, \gamma)\)以外の項の行列を計算します。
def calc_AB(point):
A = np.zeros((3,3))
B = np.zeros((3,1))
for i in range(len(point)):
x = point[i][0]
y = point[i][1]
A[0,0] += math.pow(x,2)
A[0,1] += x * y
A[0,2] += x
A[1,0] += x * y
A[1,1] += math.pow(y,2)
A[1,2] += y
A[2,0] += x
A[2,1] += y
A[2,2] += 1
p = math.pow(x,2) + math.pow(y,2)
B[0] -= x * p
B[1] -= y *p
B[2] -= p
return A,B
A,B = calc_AB(point)
\((\alpha, \beta, \gamma)\)を計算
正規方程式の項からLU分解で\((\alpha, \beta, \gamma)\)を計算します。
import scipy.linalg as linalg
def calc_abg(A,B):
LU = linalg.lu_factor(A)
x = linalg.lu_solve(LU, B)
return x
abg = calc_abg(A,B)
(a,b,r)を計算
以下の関係から\(a,b,r)\)を計算します。
$$
\begin{eqnarray}
\alpha = -2a &\Rightarrow& a = – \alpha /2\\
\beta = -2b &\Rightarrow& b = – \beta / 2\\
\gamma = a^2 +b^2 – r^2 &\Rightarrow& r = \sqrt{|a^2 + b^2 – \gamma|}
\end{eqnarray}
$$
def calc_abr(abg):
a_opt = - abg[0,0] / 2
b_opt = - abg[1,0] / 2
r_opt = math.sqrt(abs(math.pow(a_opt,2) + math.pow(b_opt,2) - abg[2,0]))
return a_opt, b_opt, r_opt
a_opt, b_opt, r_opt = calc_abr(abg)
図にplotして確認
import matplotlib.pyplot as plt
import matplotlib.patches as patches
np_point = np.array(point)
fig, ax = plt.subplots(figsize=(4,4))
plt.plot(np_point[:,0], np_point[:,1], 'o')
ax.set_aspect('equal')
ax.set_xlabel('x')
ax.set_ylabel('y')
circle = patches.Circle([a_opt, b_opt], radius=r_opt, fill=False)
ax.add_patch(circle)
plt.show()
最小二乗法で求めたパラメータで描いた円形と、ポイントデータの5点を一緒に描きました。線上にぴったりポイントデータが乗っているので、最小二乗法でパラメータ\((a,b,r)\)が求まったといえますね。

評価関数を計算する
最後に評価関数 \(J\)をポイントデータとパラメータから計算してみます。
$$
J = \frac{1}{2} \sum_{i=1}^{n} \bigl( (x_i – a)^2 + (y_i – b)^2 – r^2 \bigr) ^2
$$
J = 0
for i in range(len(point)):
x = point[i][0]
y = point[i][1]
J += math.pow(math.pow(x-a_opt,2)+math.pow(y - b_opt,2) - math.pow(r_opt,2),2)
J = J/2
print(J) # 出力 : 1.1955344790805478e-25
結果が1.1955\(\times 10^{-25}\)となったので、評価関数を最小化できたと言えます。
ランダムなポイントデータから円のパラメータを求める
綺麗に作成したポイントデータからパラメータを計算できたので、ポイントデータをランダムに生成して円を推定してみました。
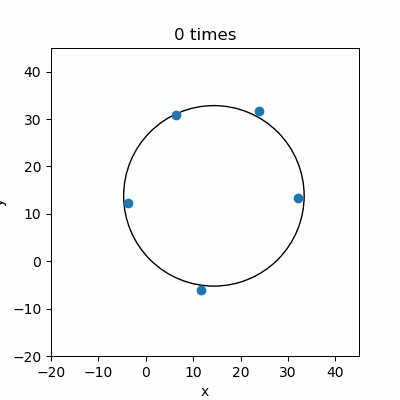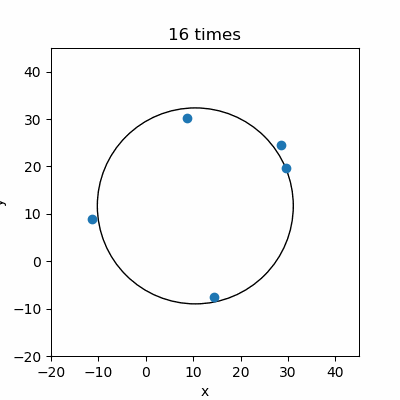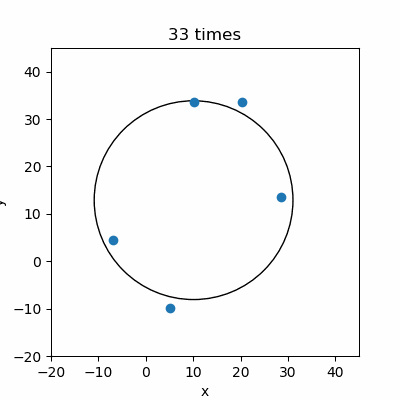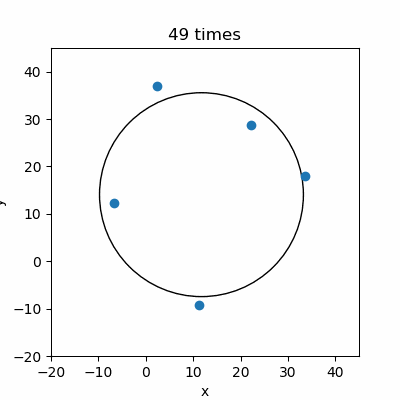
ポイントデータはバラついていますが、推定した円のパラメータをもとに描いた円は大体ポイントデータに近いですね。
線形の方式で円のパラメータを計算できたので、次は非線形最小二乗法を使って円のパラメータを計算してみます。
コメント