“これなら分かる 最適化数学”の第4章にちょっとだけ載っている非線形最小二乗法を円の方程式のパラメータ推定に当てはめてみます。ガウス・ニュートン法、レーベンバーグ・マーカート法ではなく、近似無しで行ってみます。
最小二乗法で円のパラメータを推定したときは、評価関数\(J\)を非線形から線形化して行いました。非線形最小二乗法ではこれを線形化しないで求めていきます。
線形と非線形について
円の方程式である(1)式は、求めたいパラメータの\((a,b,r)\)の2乗項があります。このためパラメータと\((a,b,r)\)と変数\((x,y)\)がパラメータに関して線形結合の形になっていません。
$$
(x-a)^2 + (y – b)^2 = r^2 \tag{1}
$$
線形であるとは
線形結合であるとは、例えば(2)式のように、パラメータ\((a,b)\)に関して行列の形で表せるものです。
$$
ax_i^2 + bx_i = 1 \rightarrow \left[\begin{array}{cc} x_i^2 & x_i\end{array}\right]\left[\begin{array}{c} a \\ b \end{array}\right] = 1 \tag{2}
$$
変数\(x_i\)を複数の測定データとし、パラメータ\((a,b)\)を求めるための評価関数\(J\)を(3)式にします。
$$
J = \frac{1}{2} \sum_{i=1}^{N} ( a x_i^2 + b x_i – 1) ^2 \tag{3}
$$
この評価関数\(J\)を\((a,b\)それぞれで偏微分しゼロとすると、正規方程式は(4)式になります。
$$
\begin{eqnarray}
\frac{\partial J} { \partial a} &=& \sum_{i=0}^N x_i^2 ( a x_i^2 + b x_i -1) =\sum_{i=0}^N ( a x_i^4 + b x_i^3 – x_i^2)= 0 \\
\frac{\partial J}{\partial b} &=& \sum_{i=0}^N x_i ( a x_i^2 + b x_i -1) = \sum_{i=0}^N ( a x_i^3 + b x_i^2 – x_i) = 0
\end{eqnarray} \tag{4}
$$
これを行列の形式で表すと、(5)式になるので、逆行列やLU分解で\((a,b)\)を求めることが出来ます。
$$
\left[\begin{array}{cc}
\sum_{i=0}^N x_i^4 & \sum_{i=0}^N x_i^3\\
\sum_{i=0}^N x_i^3 & \sum_{i=0}^N x_i^2
\end{array}\right]
\left[\begin{array}{c}
a \\ b
\end{array}\right]=
\left[\begin{array}{c}
\sum_{i=0}^N x_i^2 \\ \sum_{i=0}^N x_i
\end{array}\right] \tag{5}
$$
このような行列の形にして解ける問題が線形です。
非線形とは
線形に対して非線形とは、求めたいパラメータを(5)式のような行列の形で表せられないものとなります。
円の方程式を展開すると(6)式になるので、(5)式のようには出来ませんよね。
$$
(x_i – a)^2 + (y_i – b)^2 – r^2 = x_i^2 – 2a x_i + a^2 + y_i^2 -2b y_i +b^2 – r^2 \tag{6}
$$
例えば評価関数\(J\)を(7)式にようにし、\(a\)で微分すると(8)式になります。
$$
J = \frac{1}{2} \sum_{i=1}^{N} ( x_i^2 – 2a x_i + a^2 + y_i^2 -2b y_i +b^2 – r^2 ) ^2 \tag{7}
$$
$$
\frac{\partial J}{\partial a} = \sum_{i=1}^{N} (-2 x_i + 2a) ( x_i^2 – 2a x_i + a^2 + y_i^2 -2b y_i +b^2 – r^2 ) \tag{8}
$$
この(8)式から\(a\)の項は3乗項、2乗項、1乗項とさらに多くなってしまいました。\(J\)を\(b,r\)で微分しても同じような結果になるので、やっぱり\((a,b,r)\)の行列の形で表すことは出来ないことが分かります。
このような非線形の式において、\(x,y\)をデータとして、そこからパラメータ\((a,b,r)\)を求めることを非線形最小二乗法といいます。
円のパラメータを最小二乗法で求めたように、うまく変換を行えば線形最小二乗法でもできますが、今回はこのままの式の形で求めてみます。
非線形最小二乗法
円の方程式のパラメータのように非線形な方程式を最小二乗法で求める一つの方法はニュートン法です。
ニュートン法は式をテイラー展開して求めます。1次までの展開では式を直線近似、2次までの展開では式を2次曲線で近似したことになります。
2変数のテイラー展開
関数 \(f(x_1, x_2)\)上のある点\((\bar x_1, \bar x_2)\)から\((\delta x_1 , \delta x_2)\)離れた点\(f(\bar x_1 + \delta x_1, \bar x_2 + \delta x_2)\)は(9)式で表す事がが出来ます。
$$
f(\bar x_1 + \delta x_1, \bar x_2 + \delta x_2) = f(\bar x_1 , \bar x_2) + \sum_{i=1}^{2} \frac{ \partial f(\bar x_1, \bar x_2)}{\partial x_i}\delta x_i + \frac{1}{2} \sum_{i,j=1}^{2} \frac{ \partial^2 f(\bar x_1, \bar x_2)}{\partial x_i \partial x_j} \delta x_i \delta x_j \tag{9}
$$
(9)式を1次微分まで利用すると、\(f(x) = 0\)(関数値がゼロ)となる\(x\)を探すニュートン法になります。
(9)式を2次微分まで利用すると、\(f^\prime(x) = 0\)(関数の傾きがゼロ)となる\(x\)を探すニュートン法になります。
非線形最小二乗法では評価関数の最小または最大値を探索する問題なので、関数の傾き(勾配)がゼロとなるパラメータを探す、2次微分を利用するニュートン法を用います。
円のパラメータをニュートン法で求める
評価関数の設定
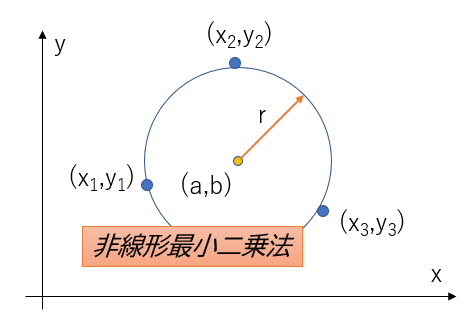
設定として下図のように3点のデータからパラメータ\((a,b,r)\)を求めるようにします。
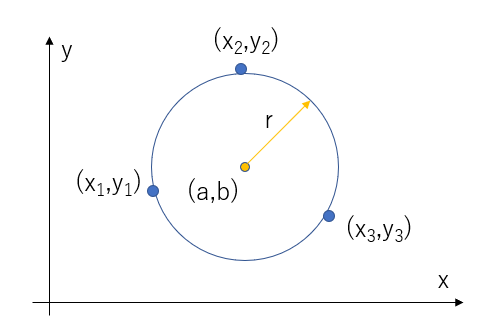
円の方程式をデータ\((x_i, y_i), i\in(1, 2,3) \)から求めたパラメータ\((a,b,r)\)が最小になるようにしたいので、評価関数\(J\)を(10)式のようにします。
$$
J = \frac{1}{2}\sum_i^3\bigl( (x_i-a)^2 + (y_i – b)^2 – r^2 \bigr)^2 \tag{10}
$$
この式にニュートン法を適用します。パラメータ\((a,b,r)\)は変数とみなせるので、多変数のニュートン法を適用します。
多変数のニュートン法は勾配とヘッセ行列が必要なので、それぞれの式を計算します。
勾配 \(\nabla J\)の計算
\(J\)をパラメータ\((a,b,r)\)のそれぞれで1階微分を行ったものが勾配です。
$$
\begin{eqnarray}
\frac{\partial J}{\partial a} &=& \sum_{\alpha=1}^3 \biggl( \bigl( (x_\alpha – a) ^2 + (y_\alpha – b) ^2 – r^2 \bigr) \bigl( -2 (x_\alpha – a) \bigr) \biggr)
\\
\frac{\partial J}{\partial b} &=& \sum_{\alpha=1}^3 \biggl( \bigl( (x_\alpha – a) ^2 + (y_\alpha – b) ^2 – r^2 \bigr) \bigl( -2 (y_\alpha – b) \bigr) \biggr)
\\
\frac{\partial J}{\partial r} &=& \sum_{\alpha=1}^3 \biggl( \bigl( (x_\alpha – a) ^2 + (y_\alpha – b) ^2 – r^2 \bigr) \bigl( -2 r \bigr) \biggr)
\end{eqnarray} \tag{11}
$$
複雑な関数の微分は、以下のように合成関数の微分を用いると簡単に求まります。
$$
f(a) = (x-a)^2 , C = x-aとすると \rightarrow (x-a)^2 = C^2 = f(a)\\
\frac{d f(a) }{ da} = \frac{d f(a) } { d C} \frac{d C}{d a} = 2C \times -1 = -2(x-a)
$$
ヘッセ行列 \(\boldsymbol{H}\)の計算
ヘッセ行列\(\boldsymbol{H}\)は勾配\(\nabla J\)を\((a,b,r)\)のそれぞれで微分したものです。
$$
{\bf H} = \left[
\begin{array}{ccc}
\partial ^2 J / \partial a^2 & \partial ^2 J / \partial a \partial b & \partial ^2 J / \partial a \partial r \\
\partial ^2 J / \partial a \partial b & \partial ^2 J / \partial b^2 & \partial ^2 J / \partial b \partial r \\
\partial ^2 J / \partial a \partial r & \partial ^2 J / \partial b \partial r & \partial ^2 J / \partial r^2 \
\end{array}
\right]
$$
以下の微分法則で(11)式を微分します。
$$
\frac{d}{d x}\big( f_1(x)f_2(x) \big) = \frac{d f_1(x)}{d x} f_2(x) + f_1(x) \frac{d f_2(x)}{d x}
$$
ちょっと長いですが、ヘッセ行列の各項目は以下のように計算できます。
$$
\begin{eqnarray}
\frac{\partial ^2 J}{\partial a^2} &=& \sum_{\alpha=1}^{3} \biggl( \bigl( -2 (x_\alpha -a) \bigr) \bigl( -2 (x_\alpha -a) \bigr) + \bigl ( (x_\alpha – a) ^2 + (y_\alpha -b)^2 – r^2 \bigl) \cdot 2 \biggr) \\ &=&\sum_{\alpha=1}^{3} \biggl( 6(x_\alpha – a) ^2 + 2(y_\alpha -b)^2 – 2r^2 \biggr)\\
\frac{\partial ^2 J}{\partial a \partial b} &=& \sum_{\alpha=1}^{3} \biggl( \bigl( -2 (y_\alpha -b) \bigr) \bigl( -2 (x_\alpha -a) \bigr) + \bigl ( (x_\alpha – a) ^2 + (y_\alpha -b)^2 – r^2 \bigl) \cdot 0 \biggr) \\&=& \sum_{\alpha=1}^{3} \biggl( 4 (y_\alpha -b) (x_\alpha -a)\biggr)\\
\frac{\partial ^2 J}{\partial a \partial r} &=& \sum_{\alpha=1}^{3} \biggl( \bigl( -2 r \bigr) \bigl( -2 (x_\alpha -a) \bigr) + \bigl ( (x_\alpha – a) ^2 + (y_\alpha -b)^2 – r^2 \bigl) \cdot 0 \biggr) \\&=& \sum_{\alpha=1}^{3} \biggl( 4 r (x_\alpha -a) \biggr)\\
\frac{\partial ^2 J}{\partial b^2} &=& \sum_{\alpha=1}^{3} \biggl( \bigl( -2 (y_\alpha -b) \bigr) \bigl( -2 (y_\alpha -b) \bigr) + \bigl ( (x_\alpha – a) ^2 + (y_\alpha -b)^2 – r^2 \bigl) \cdot 2 \biggr)\\ &=& \sum_{\alpha=1}^{3} \biggl( 2(x_\alpha – a) ^2 + 6(y_\alpha -b)^2 – 2r^2 \biggr)\\
\frac{\partial ^2 J}{\partial b \partial r} &=& \sum_{\alpha=1}^{3} \biggl( \bigl( -2 r \bigr) \bigl( -2 (y_\alpha -b) \bigr) + \bigl ( (x_\alpha – a) ^2 + (y_\alpha -b)^2 – r^2 \bigl) \cdot 0 \biggr) \\&=& \sum_{\alpha=1}^{3} \biggl( 4 r (y_\alpha -b) \biggr)\\
\frac{\partial ^2 J}{\partial r^2} &=& \sum_{\alpha=1}^{3} \biggl( \bigl( -2 r \bigr) \bigl( -2 r \bigr) + \bigl ( (x_\alpha – a) ^2 + (y_\alpha -b)^2 – r^2 \bigl) \cdot -2 \biggr) \\&=& \sum_{\alpha=1}^{3} \biggl( -2(x_\alpha – a) ^2 + -2(y_\alpha -b)^2 + 6 r^2 \biggr)
\end{eqnarray}
$$
ニュートン法の計算ステップ
では求めた勾配\(\nabla J\)とヘッセ行列\(\boldsymbol{H}\)を使ったニュートン法を確認します。今回は求めたいパラメータは\(a,b,r\)の3つです。ということでニュートン法の計算ステップは次のようになります。
Step 1 \(u_0 = a_0, b_0, r_0\)を初期値とする
Step 2 \( {\bf u} = u_0 \)とする
Step 3 \({\bf u}\)における\(\nabla J, {\bf H}\)を計算する
Step 4 \({\bf H} \Delta u = – \nabla J\)から\(\Delta u\)を計算する
Step 5 \({\bf u} \leftarrow {\bf u} + \Delta u\)と更新する
Step 6 \(|| \Delta u || < \sigma\)なら終了し\({\bf u}\)を解とする。そうでないなら、Step 3へ
step 4の計算はLU分解で行います。
プログラムで計算 – Python
ニュートン法のクラス
コンストラクタで\((x,y)\)の行列を設定し、\(search\)関数で、パラメータをニュートン法で探索するクラスとします。\(\nabla J\)と\(\boldsymbol{H}\)はこのクラスに直接実装しています。
import numpy as np
import scipy.linalg as linalg
class Newton_circle:
def __init__(self, points):
self.points = points
def __dJda(self, u, point):
return ( (point[0]-u[0])**2 + (point[1] - u[1])**2 - u[2]**2 ) * (-2*(point[0]-u[0]) )
def __dJdb(self, u, point):
return ( (point[0]-u[0])**2 + (point[1] - u[1])**2 - u[2]**2 ) * (-2*(point[1]-u[1]) )
def __dJdr(self, u, point):
return ( (point[0]-u[0])**2 + (point[1] - u[1])**2 - u[2]**2 ) * (-2*u[2])
#勾配の計算
def __nabla_J(self, u):
djda = 0
djdb = 0
djdr = 0
for i in range(len(self.points)):
djda = djda + self.__dJda(u, self.points[i])
djdb = djdb + self.__dJdb(u, self.points[i])
djdr = djdr + self.__dJdr(u, self.points[i])
return np.array([djda, djdb, djdr])
def __ddJdada(self, u, point):
return ( 6*(point[0] - u[0])**2 + 2*(point[1] - u[1])**2 - 2*u[2]**2 )
def __ddJdadb(self, u, point):
return ( 4*(point[1] - u[1])*(point[0] - u[0]) )
def __ddJdadr(self, u, point):
return ( 4*u[2]*(point[0] - u[0]) )
def __ddJdbdb(self, u, point):
return ( 2*(point[0] - u[0])**2 + 6*(point[1] - u[1])**2 - 2*u[2]**2 )
def __ddJdbdr(self, u, point):
return ( 4*u[2]*(point[1] - u[1]) )
def __ddJdrdr(self, u, point):
return ( -2*(point[0] - u[0])**2 -2*(point[1] - u[1])**2 + 6*u[2]**2 )
#ヘッセ行列の計算
def __HessianMatrix(self, u):
m00 = 0
m01 = 0
m02 = 0
m11 = 0
m12 = 0
m22 = 0
for i in range(len(self.points)):
m00 = m00 + self.__ddJdada(u, self.points[i])
m01 = m01 + self.__ddJdadb(u, self.points[i])
m02 = m02 + self.__ddJdadr(u, self.points[i])
m11 = m11 + self.__ddJdbdb(u, self.points[i])
m12 = m12 + self.__ddJdbdr(u, self.points[i])
m22 = m22 + self.__ddJdrdr(u, self.points[i])
return np.array([[m00, m01, m02], [m01, m11, m12], [m02, m12, m22]])
#評価関数 J
def calc_J(self, u):
p = 0
for i in range(len(self.points)):
p+=( (self.points[i,0]-u[0])**2 + (self.points[i,1] - u[1])**2 - u[2]**2)**2
return p/2
#ニュートン法で探索
def search(self, initial_u, sigma):
# Step 2
u = initial_u
while True:
# Step 3
nablaJ = self.__nabla_J(u)
Hessian = self.__HessianMatrix(u)
# Step 4
LU = linalg.lu_factor(Hessian)
delta_u = linalg.lu_solve(LU, -nablaJ)
# step 5
u = u + delta_u
# step 6
norm = np.sqrt(np.sum(delta_u**2))
if(norm < sigma):
break
# 評価関数J 計算
J = self.calc_J(u)
return u, J
データの作成
アルゴリズムの確認のため、円の中心:\(a, b\)と、半径:\(r\)と角度\(\theta\)から3点のデータを作成し、そこへ収束するか確認します。設定値は\((a,b,r) = (2,2,10)\)です。
import math
def cal_point(a, b, r, theta):
px = a + r * math.cos(math.radians(theta))
py = b + r * math.sin(math.radians(theta))
return [px, py]
a = 2
b = 2
r = 10
points = np.array([cal_point(a,b,r, 0), cal_point(a,b,r, 120), cal_point(a,b,r, 240)])
ニュートン法でパラメータ探索
では初期値を \((a,b,r) = (-10,10,2)\)としてニュートン法でパラメータを探してみます。
# 探索クラスの作成
nonlinear_search = Newton_circle(points)
# 初期パラメータの設定
u = np.array([-10,10,2])
#収束判定
sigma = 0.0001
#ニュートン法でパラメータ探索
opt_u, opt_J = nonlinear_search.search(u, sigma)
print("u:{0}".format(opt_u))
print("J:{0}".format(opt_J))
とすると結果は\(r\)がゼロになってしまいました。
u:[ 2.00000000e+00 2.00000000e+00 -1.86347248e-20] J:15000.000000000004
次は初期値を \((a,b,r) = (10,-10,10)\)として計算してみました。結果はやはり\(r\)がゼロになります。
u:[ 2.00000000e+00 2.00000000e+00 -5.15605896e-17] J:15000.000000000004
今度は初期値を \((a,b,r) = (10,-3,10)\)として計算してみました。今度は\(r\)の結果が設定値の10になったので、無事にパラメータ探索が出来ました。
u:[ 2. 2. 10.] J:9.162330732955033e-19
\((a,b)\)はデータ作成で使用した\(2,2\)へ毎回収束しましたが、\(r\)はなかなか収束しませんでした。どうやら局所解が10以外にもあるようです。ということで図に描いてそもそも評価関数\(J\)はどのような形なのか見てみます。
評価関数\(J\)の形
a-b平面の形
評価関数\(J\)は\(J(a,b,r)\)の関数です。3次元のプロットはぱっと見て理解が難しいため、まず、\(r\)を固定した\((a,b)\)平面で形を描いてみます。
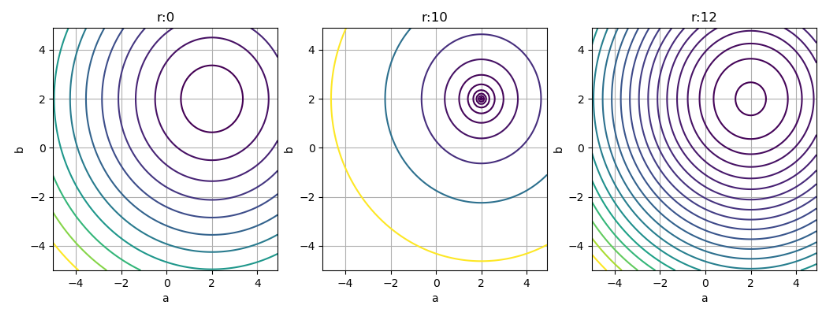
\(r\)を(0, 10, 12)の3つに固定して評価関数\(J\)のa-b平面を描きました。この図からa-b平面は2次関数のようなっているので、\(r\)がどの点でも(2,2)に収束することが分かりますね。
それから\(r\)方向で比較すると、\(r=10\)のところが密になっているので、ここに極値があるように見えます。でも\(r=0\)で収束する結果もありました。
そこで\(a = 1,2,3\)と固定してb-r平面を描いて\(r\)方向の変化をもっと詳しく見てみます。
b-r平面
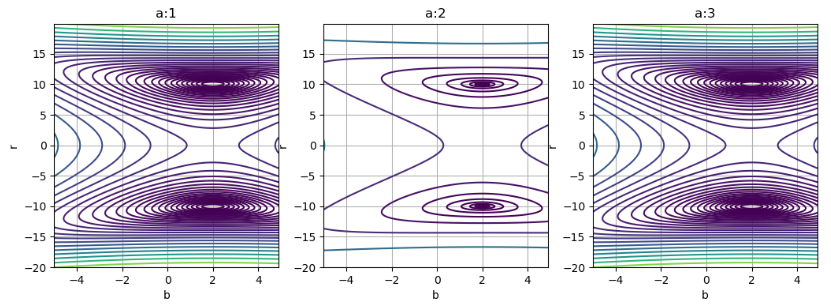
\(a = 1,2,3\)と固定してb-r平面を描きました。この図の縦軸が\(r\)です。
図を観察すると、設定した\(r=10\)以外に\(r=0, -10\)に極値があるようです。
では、\(a=b=2\)と固定したときの\(r\)による変化も図で描き、\(r=-10, 0, 10\)の点がそれぞれどのようになっているのか詳しく見てみましょう。
r-J平面
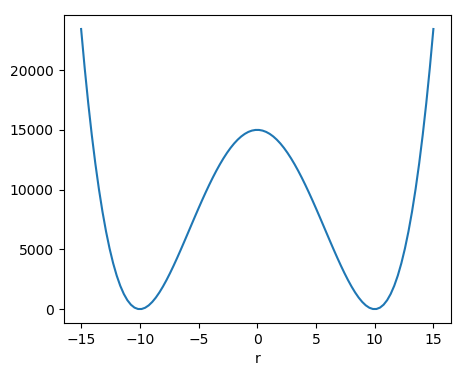
\((a,b) =(2,2)\)と固定して、r-J平面を描きました。この図の縦軸は評価関数\(J\)です。この図のように\(r\)に関しては4次曲線となっているので、局所解が \(r=-10, 0, 10\)のどこかになること言えます 。
ランダムなデータから円のパラメータを推定
r-J平面から\(r\)の局所解は \(r=-10, 0, 10\) のどこかにあることが分かりました。1次変数のニュートン法では、極値に近い方向から探索を始めると、その極値へ収束することを確認しました。
今回はランダムは4点のデータから円のパラメータ\((a,b,r)\)を推定するので、\(r\)の初期値を大きめに振っておきます。これは、\(r\)は負とゼロではないからです。
推定結果
ニュートン法の初期値を\((a,b,r) = (1,1,100)\)とします。そして、4つのランダムなデータから円のパラメータを推定します。
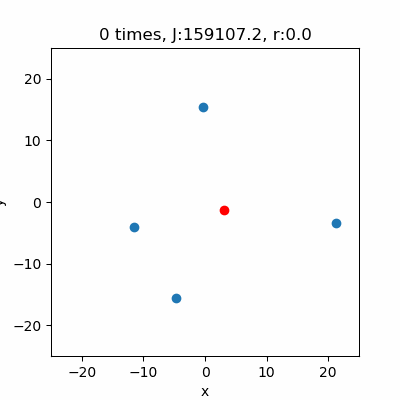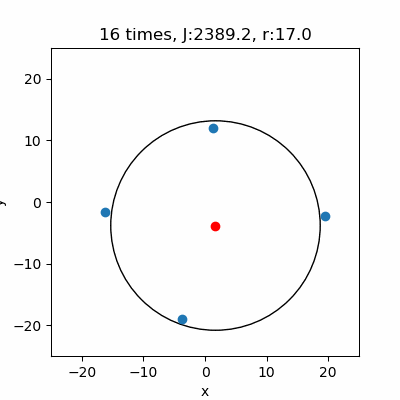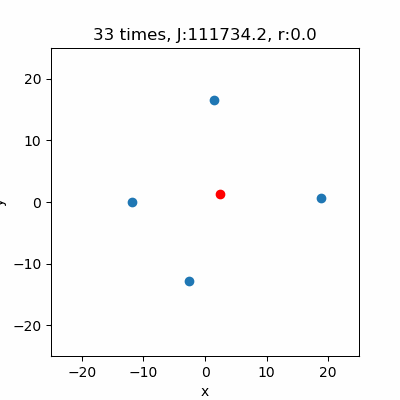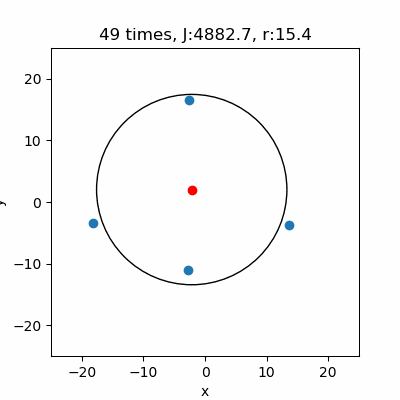
図の赤点は推定した\((a,b)\)の値です。毎回中心になるような所にプロットできていますね。それに対し\(r\)は結構ゼロになっていることがあるので、円が描かれたり、\(r\)がゼロとなり描かれなかったりしています。ただ単に\(r\)の初期値を大きくすればいいという事でもなさそうです。
円のパラメータをニュートン法で求めるためのアルゴリズム
一気に\((a,b,r)\)を求めようとするとさっきの結果のように、\(r\)がゼロになります。でも\((a,b)\)は毎回正しく推定できていました。ということで次のような手順で\((a,b,r)\)を求めます。
step 1. \(r_0=0\)にして初期値\((a_0, b_0, r_0)\)から\((a,b)\)を探索する
step 2. 探索した\((a,b)\)から各データまでの距離の平均 \(\bar {r}\)を計算し、\(a, b, \bar{r}\)を初期値にして、\(r\)を計算する
このようにすると、\(r\)の探索はstep 1で収束した\((a,b)\)を使うので、r-J平面で行われることになります。そして\(r\)探索の初期値は下の図の範囲で示した\(r\)の真のパラメータに近いところから始めることが出来るので、0には収束しないはずです。
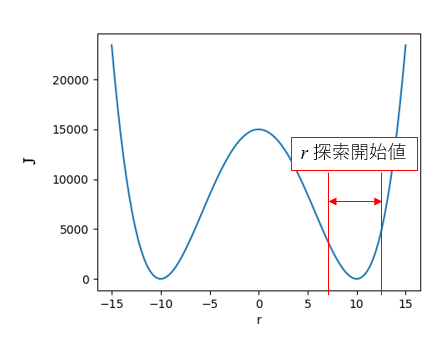
このアルゴリズムで\((a,b,r)\)を推定した結果です。あまりにも円にならないようなデータである場合は\(r\)がゼロになることがありますが、それ以外は良好に円のパラメータ\( (a,b,r)\) を推定することが出来ています。
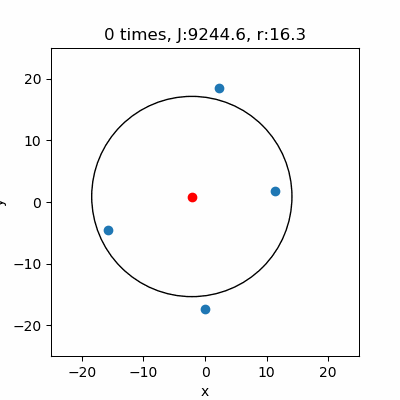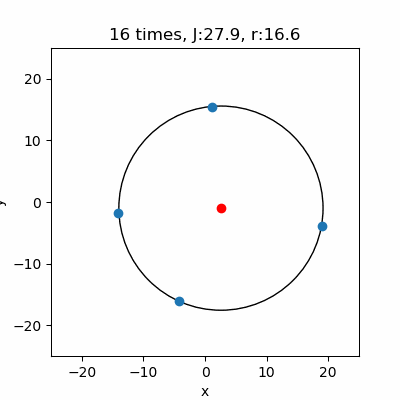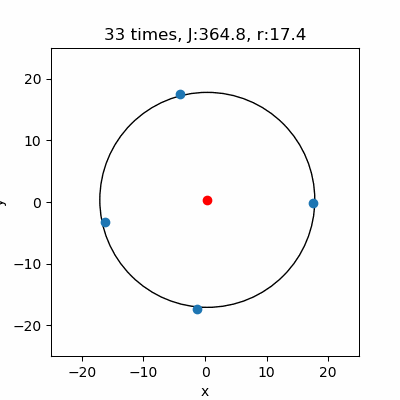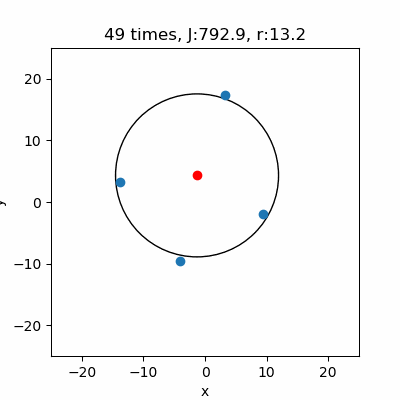
小手先のテクニック的な方法でアルゴリズムを組んでみましたが、これで非線形最小二乗法を理解することが出来ました。
円のパラメータ推定に関して
線形、非線形の両方で円のパラメータを推定してみましたが、両方とも何らかの変換をしないとパラメータが正しく推定できませんでした。
円の方程式に限らず、何か方程式のパラメータ推定を行う場合は、式の意味や形を考えて行わないと上手は収束計算が出来ないということでしょうね。

コメント