ベルヌーイ分布に従う確率変数\(X\)の\(n\)回の合計は2項分布で表すことが出来ます。
確率分布、期待値、分散
確率分布
2項分布に従う確率変数\(X\)は次の確率関数の式に従い分布します。
\(\theta\)が母数で、\(x\)が結果の回数の合計です。
$$
f(x | \theta) = {}_n \mathrm{C} _x \theta^x (1-\theta)^{n-x}
$$
例えば、本のページをランダムに何回か開いて、そのページにイラスト/図が載っている回数は確率は、\(n\)、\(\theta\)、\(x\)を次のように考えて計算できます。
\(n\) : 本を開く回数
\(\theta\) : 開いたページにイラスト/図が載っている確率
\(x\) : 本を開いた回数のうち、イラストが載っていた回数
\(n = 3\)、\(\theta = 0.1\)とすると、\(x\)をパラメータとして
$$
\begin{eqnarray}
x = 0 \Rightarrow&& {}_3 \mathrm{C} _0 \theta^0 (1-\theta)^{3-0} = 1 \cdot (1-\theta)^3 = 0.729\\
x = 1 \Rightarrow&& {}_3 \mathrm{C} _1 \theta^1 (1-\theta)^{3-1} = 3 \cdot \theta (1-\theta)^2 = 0.243\\
x = 2 \Rightarrow&& {}_3 \mathrm{C} _2 \theta^2 (1-\theta)^{3-2} = 3 \cdot \theta^2 (1-\theta)^1 = 0.027 \\
x = 3 \Rightarrow&& {}_3 \mathrm{C} _3 \theta^3 (1-\theta)^{3-3} = 1 \cdot \theta^3 = 0.001\\
\end{eqnarray}
$$
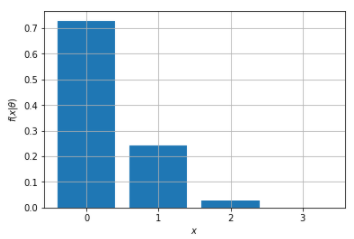
例えば、本のページを開いて3回ともイラストが無い確率は約73%となります。
期待値と分散
2項分布の期待値\(E[X]\)と分散\(V[X]\)は次の式です。
$$
\begin{eqnarray}
E[X] &=& n \theta \\
V[X] &=& n \theta (1 – \theta)
\end{eqnarray}
$$
ベルヌーイ分布の期待値が\(n\)倍されているだけですね。
期待値と分散の導出
期待値 \(E[X]\)の導出
2項分布の確率変数\(X\)はベルヌーイ分布に従う確率変数\(X_1, X_2 \cdots, X_n\)の和であり、それぞれの確率変数は互いに独立であるとすると、
$$
\begin{eqnarray}
E[X] &=& E[X_1 + X_2 + \cdots + X_n] \\
&=& E[X_1] + E[X_2] + \cdots + E[X_n]\\
&=& \theta + \theta + \cdots + \theta \\
&=& n \theta
\end{eqnarray}
$$
分散\(V[X]\)の導出
期待値と同じく、ベルヌーイ分布に従う確率変数\(X_1, X_2, \cdots ,X_n\)の和で考えると、
$$
\begin{eqnarray}
V[X] &=& V[X_1 + \cdots X_n] \\
&=& V[X_1] + \cdots + V[X_n] \\
&=& \theta(1-\theta) + \cdots + \theta(1-\theta) \\
&=& n \theta(1-\theta)
\end{eqnarray}
$$

コメント