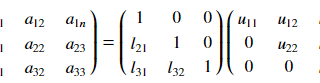 数値計算
数値計算 どのようにA行列をLU行列へと分解するのか – アルゴリズム –
LU分解では、A行列をL行列とU行列へ分解することが必要です。このとき、単純に分解していてはゼロ割になっていしまうことがあり、Pivotという方法で行列を入替えながら分解していくことが求められます。なかなか複雑な方法なので、理解が難しいですがPythonコードとともにその理論と実装を説明します。
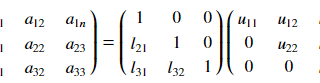 数値計算
数値計算 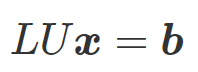 数値計算
数値計算  数値計算
数値計算 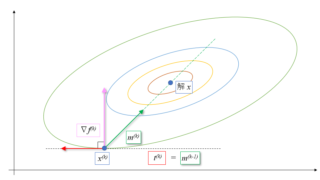 数値計算
数値計算  数値計算
数値計算 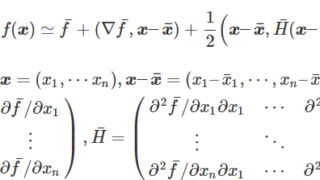 数値計算
数値計算 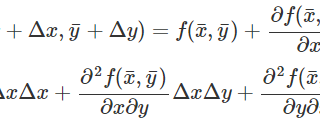 数値計算
数値計算 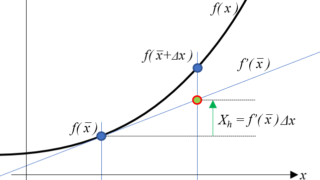 数値計算
数値計算  数値計算
数値計算  数値計算
数値計算