連立方程式 \(A \boldsymbol{x} = \boldsymbol{b} \) の解\( \boldsymbol{x} \)を求めるときに、逆行列を使った\( \boldsymbol{x} = A^{-1} \boldsymbol{b} \)という形以外に、\( A = LU\)と分解して解 \( \boldsymbol{x} \) を求めるLU分解があります。このように分解すると何がうれしいのでしょうか?具体的に計算してみましょう。
LU分解とは何か
LUの形
LU分解は行列\(A\)を(1)式のように、下三角行列\(L\)と上三角行列\(U\)に分解するものです。
$$
A= LU =
\left(\begin{array}{cccc}
1 & 0 & 0 & 0 \\
l_{21} & 1 & 0 & 0 \\
l_{31} & l_{32} & 1 & 0 \\
l_{41} & l_{42} & l_{43} & 1
\end{array}\right)
\left(\begin{array}{cccc}
u_{11} & u_{12} & u_{13} & u_{14} \\
0 & u_{22} & u_{23} & u_{24} \\
0 & 0 & u_{33} & u_{34} \\
0 & 0 & 0 & u_{44}
\end{array}\right) \tag{1}
$$
解を求める手順
もともと方程式は \(A \boldsymbol{x} = \boldsymbol{b} \) という形をしていたので、分解したLUを代入すると(2)式になります。
$$
LU \boldsymbol{x} = \boldsymbol{b} \tag{2}
$$
ここで、(3)式を定義することで、(2)式は(4)式になります。
$$
U\boldsymbol{x} = \boldsymbol{z} \tag{3}
$$
$$
L\boldsymbol{z} = \boldsymbol{b} \tag{4}
$$
この(3)式と(4)式の関係から、次の2ステップで \( \boldsymbol{x} \)を計算できます。
Step 1: \( L\boldsymbol{z} = \boldsymbol{b} \)から、\( \boldsymbol{z} \)を計算
Step 2: \( U\boldsymbol{x} = \boldsymbol{z} \)から、 \( \boldsymbol{x} \)を計算
なんだか周りくどいことをしているように見えますよね?でも(1)式のように分解することで、\(A^{-1}\)を計算しなくても、簡単なアルゴリズムで解を計算することが出来るんです。

そもそもLUへの分解はどうするの?
という疑問はあると思いますが、それは一旦置いて、具体的に計算してみましょう。
具体的に計算してみる
Step1 とStep2を計算するために、(5)式、(6)式を定義して計算します。
$$
\left(\begin{array}{cccc}
1 & 0 & 0 & 0 \\
l_{21} & 1 & 0 & 0 \\
l_{31} & l_{32} & 1 & 0 \\
l_{41} & l_{42} & l_{43} & 1
\end{array}\right)
\left(\begin{array}{c}
z_1 \\ z_2 \\ z_3 \\ z_4
\end{array}\right)
=
\left(\begin{array}{c}
b_1 \\ b_2 \\ b_3 \\ b_4
\end{array}\right)
\tag{5}
$$
$$
\left(\begin{array}{cccc}
u_{11} & u_{12} & u_{13} & u_{14} \\
0 & u_{22} & u_{23} & u_{24} \\
0 & 0 & u_{33} & u_{34} \\
0 & 0 & 0 & u_{44}
\end{array}\right)
\left(\begin{array}{c}
x_1 \\ x_2 \\ x_3 \\ x_4
\end{array}\right)
=
\left(\begin{array}{c}
z_1 \\ z_2 \\ z_3 \\ z_4
\end{array}\right)
\tag{6}
$$
Step 1 : \(L \boldsymbol{z} = \boldsymbol{b}\)から \(\boldsymbol{z}\)を求める
$$
\left(\begin{array}{cccc}
1 & 0 & 0 & 0 \\
l_{21} & 1 & 0 & 0 \\
l_{31} & l_{32} & 1 & 0 \\
l_{41} & l_{42} & l_{43} & 1
\end{array}\right)
\left(\begin{array}{c}
z_1 \\ z_2 \\ z_3 \\ z_4
\end{array}\right)
=
\left(\begin{array}{c}
b_1 \\ b_2 \\ b_3 \\ b_4
\end{array}\right) \tag{5}
$$
(5)式を1行目から計算していくと・・・
$$
\begin{eqnarray}
&&z_1 = b_1 \\
l_{21} z_1 + z_2 = b_2 &\Rightarrow& z_2 = b_2 – l_{21} z_1 \\
l_{31} z_1 + l_{32} z_2 + z_3 = b_3 &\Rightarrow& z_3 = b_3 – l_{31} z_1 – l_{32} z_2 \\
l_{41} z_1 + l_{42} z_2 + l_{43} z_3 + z_4 = b_4 &\Rightarrow& z_4 = b_4 – l_{41} z_1 – l_{42} z_2 – l_{43} z_3
\end{eqnarray}
$$
\(L\)が対角要素を\(1\)とした下三角行列の形をしているので、一定の手順で計算することが出来ます。
1行目の計算は行列の形から直ぐに求められますね。この計算で\(z_1\)が求まります。次に2行目を計算しますが、この時\(z_2\)はさっき求めた\(z_1\)を使って計算ができます。そして3行目から、\(z_3\)を既に計算した\(z_2、z_1\)を使い求めます。最後の4行目から\(z_4\)を既に求めた\(z_3、z_2、z_1\)から計算します。
今の手順を一般化して書くと(7)式になるので、\(i\)を1から昇順(1,2,3,\(\cdots\))と計算していけば、\(L \boldsymbol{z} = \boldsymbol{b} \)の解\( \boldsymbol{z} \)が計算できます。
$$
z_i = b_i – \sum_{j=1}^{i-1} l_{i j} z_{j} \tag{7}
$$
Step 2: \(U \boldsymbol{x} = \boldsymbol{z}\)から \(\boldsymbol{x}\)を求める
$$
\left(\begin{array}{cccc}
u_{11} & u_{12} & u_{13} & u_{14} \\
0 & u_{22} & u_{23} & u_{24} \\
0 & 0 & u_{33} & u_{34} \\
0 & 0 & 0 & u_{44}
\end{array}\right)
\left(\begin{array}{c}
x_1 \\ x_2 \\ x_3 \\ x_4
\end{array}\right)
=
\left(\begin{array}{c}
z_1 \\ z_2 \\ z_3 \\ z_4
\end{array}\right)
\tag{6}
$$
この(6)式を下の行から計算していくと・・・
$$
\begin{eqnarray}
u_{44} x_{4} = z_4 &\Rightarrow& x_{4} = \frac{1}{u_{44}}z_4 \\
u_{33} x_3 + u_{44} x_4 = z_3 &\Rightarrow& x_3 = \frac{1}{u_{33}} \bigl(z_3 – u_{44} x_4\bigr) \\
u_{22} x_2 + u_{23} x_3 + u_{24} x_4 = z_2 &\Rightarrow&
x_2 = \frac{1}{u_{22}} \bigl( z_2 – u_{23} x_3 – u_{24} x_4 \bigr) \\
u_{11} x_1 + u_{12} x_2 + u_{13} x_3 + u_{14} x_4 = z_1 &\Rightarrow&
x_1 = \frac{1}{u_{11}} \bigl( z_1 – u_{12} x_2 – u_{13} x_3 – u_{14} x_4 \bigr)
\end{eqnarray}
$$
このように、\(U\)が上三角行列の形をしているので、Step 1で\(\boldsymbol{z}\)を求めた手順と同じ形で \(\boldsymbol{x}\) を求めることが出来ます。
この手順も一般化してして式にすると、(8)式となり、\(i\)を\(n\)から計算していけば、\(\boldsymbol{x}\)を求めることが出来ます。\(i\)の順番は今回の例では、\(n=4\)なので、(\(4,3,2,1\))の順番です。
$$
x_i = \frac{1}{u_{ii}}\bigl( z_i – \sum_{j=i+1}^{n} u_{i j} x_j \bigr) \tag{8}
$$
このように、\(A=LU\)と分解すれば機械的な計算で\(A \boldsymbol{x} = \boldsymbol{b}\)の方程式の解\(\boldsymbol{x}\)を計算ができます。ガウスの消去法のように考えながら解を求める方法と比べると手順が一定なのでプログラムもしやすい方法です。
計算上の問題 – ゼロ割の意味
この\(LU\)分解は手順が簡単な方法なのですが、一つ考えることがあります。それは、そもそも解が存在するのか?ということです。これは、Step 2で計算していく時に\(U\)行列の対角要素\((u_{11}, u_{22}, u_{33}, u_{44} )\)がゼロとなる場合、ゼロ割が発生してしまうと計算ができないということと一緒です。
対角要素がゼロとなるということを別の見方をすると、\(\det(U) = 0\)ということを意味しています。そして、\(A=LU\)は以下の形をしているので、\(det(A) = \det(L)\det(U)\)であり、\(det(L)=1\)から\(det(U) = 0 \)は\( \det(A) = 0\)ということを意味しています。
$$
A = LU =
\left(\begin{array}{cccc}
1 & 0 & 0 & 0 \\
l_{21} & 1 & 0 & 0 \\
l_{31} & l_{32} & 1 & 0 \\
l_{41} & l_{42} & l_{43} & 1
\end{array}\right)
\left(\begin{array}{cccc}
u_{11} & u_{12} & u_{13} & u_{14} \\
0 & u_{22} & u_{23} & u_{24} \\
0 & 0 & u_{33} & u_{34} \\
0 & 0 & 0 & u_{44}
\end{array}\right)
$$
\(det(A) = 0\)ということは、\(A\)の逆行列が存在しないということになるので、そもそも解が存在しないということになりますね。
ということで、計算途中でゼロ割が発生したら解が存在しないと判断します。
実はこのゼロ割ですが、対角要素すべてではなく、一か所がゼロとなった場合Pivotという方法で乗り切れることが出来ます。それは\(A\)行列を\(LU\)行列へ分解する手順で出てきます。
LU分解ってとても簡単に連立方程式の解を求める方法でしたね。
プログラムコード – python
LU行列から解を求める関数
import numpy as np
# step 1 計算
def solve_z(L, b):
z = np.zeros(b.shape)
for i in range(z.shape[0]):
r = 0
for j in range(0, i):
r += L[i,j] * z[j]
z[i] = b[i] - r
return z
# step 2 計算
def solve_x(U, z):
x = np.zeros(z.shape)
for i in reversed(range(x.shape[0])):
r = 0
for j in range(i + 1, x.shape[0]):
r += U[i,j] * x[j]
x[i] = (z[i] - r)/U[i,i]
return x
実行
# 行列の定義
L= np.array([[1, 0, 0],
[0.4, 1, 0],
[0.2, 0.5, 1]])
U = np.array([[5, 8, 1]
[0, 0.8, -9,4],
[0, 0, 7.5]])
b = np.array([1,2,3])
# step 1 計算
z = solve_z(L, b)
# step 2 計算
x = solve_x(U, z)
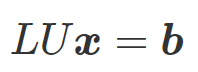
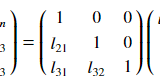

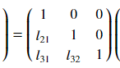
コメント